データ構造 Union-Find 木蟻本読書会

ひとりで勝手にはじめた蟻本読書会データ構造 set, map 編蟻本読書会の続きです。

Union-Find木とはグループ分けを木構造で管理するデータ構造です。このデータ構造であれば、同じグループに属するなら同じ木に属します。

要素xと要素yが同じグループに属するかどうかを判定したり、要素xの属するグループと要素yの属するグループを併合する処理を高速でおこなうことができます。

要素xと要素yが同じグループに属するかどうかは要素xと要素yのrootを比較します。同じであれば同じグループです。

Contents

1 UnionFindTreeクラスを定義する
2 UnionFindTreeクラスを使ってみる
3 応用問題
4 グラフの連結成分
- 4.1 D – New Friends

UnionFindTreeクラスを定義する

こんなクラスを定義すると便利かもしれません。

最初は各データの親は自分自身です。

前述のとおり、データが同じ木に属するのかを調べるときはデータのrootを比較するわけですが、各データが属する木を併合する場合も各データのrootを取得し、それらが異なる場合は一方を他方の直接の子にすることで処理をおこないます。そのためいかに素早くrootを取得することができるかが肝となります。

ここではデータが属する木の根を再帰で得て、経由するすべての親のrootを取得したrootで書き換えています。こうすることで素早くrootを取得することができます。

class UnionFindTree
{
    int[] parents = { }; // データxの親

    // 引数は頂点の数
    public UnionFindTree(int n)
    {
        parents = new int[n];
        for (int i = 0; i < n; i++)
            parents[i] = i; // 最初はデータxの親は自分自身である
    }

    // データxが属する木の根を再帰で得る
    public int GetRoot(int x)
    {
        if (parents[x] == x)
            return x;
        parents[x] = GetRoot(parents[x]);
        return parents[x];
    }

    // xとyの木を併合
    public void Unite(int x, int y)
    {
        int rx = GetRoot(x); //xの根
        int ry = GetRoot(y); //yの根

        // xとyの根が同じ(=同じ木にある)時はそのまま
        //xとyの根が同じでない(=同じ木にない)時：xの根rxをyの根ryにつける
        if (rx != ry)
            parents[rx] = ry;
    }

    // 2つのデータx, yが属する木が同じならtrueを返す
    public bool IsSame(int x, int y)
    {
        int rx = GetRoot(x);
        int ry = GetRoot(y);
        return rx == ry;
    }
}

class UnionFindTree

{

int[] parents = { }; // データxの親

// 引数は頂点の数

public UnionFindTree(int n)

{

parents = new int[n];

for (int i = 0; i < n; i++)

parents[i] = i; // 最初はデータxの親は自分自身である

}

// データxが属する木の根を再帰で得る

public int GetRoot(int x)

{

if (parents[x] == x)

return x;

parents[x] = GetRoot(parents[x]);

return parents[x];

}

// xとyの木を併合

public void Unite(int x, int y)

{

int rx = GetRoot(x); //xの根

int ry = GetRoot(y); //yの根

// xとyの根が同じ(=同じ木にある)時はそのまま

//xとyの根が同じでない(=同じ木にない)時：xの根rxをyの根ryにつける

if (rx != ry)

parents[rx] = ry;

}

// 2つのデータx, yが属する木が同じならtrueを返す

public bool IsSame(int x, int y)

{

int rx = GetRoot(x);

int ry = GetRoot(y);

return rx == ry;

}

UnionFindTreeクラスを使ってみる

B – Union Find

N 頂点の、単純とは限らない無向グラフを考えます。初期状態では、頂点のみが存在し、辺は全く存在せず、全ての頂点が孤立しているとします。以下の 2 種類のクエリが、Q 回与えられます。

連結クエリ：頂点 A と、頂点 B を繋ぐ辺を追加します。
判定クエリ：頂点 A と、頂点 B が、連結であるかどうか判定します。連結であれば Yes、そうでなければ No を出力します。

クエリを順番に処理し、判定クエリへの回答を出力して下さい。この際、同じ辺が何度も追加されることや、自分自身への辺が追加されることもある事に注意してください。

連結であるとは、頂点 A から頂点 B まで辺をたどって到達可能であることを意味します。 A と B が同じ頂点の場合、連結であると定義します。グラフは無向であるため、連結クエリによって頂点 A, B 間の辺が追加されると、A から B へも B から A へも辿れるようになります。

入力されるデータ
N Q
P_1 A_1 B_1
P_2 A_2 B_2
　…
P_Q A_Q B_Q
（ただし N は頂点の個数を表す整数、Q はクエリの個数を表す整数
P_i が 0 なら連結クエリ、1 なら判定クエリ
1 ≦ N ≦ 100,000
1 ≦ N ≦ 200,000）

さきほど定義したクラスを使うと以下のように書けます。

using System;
using System.Collections.Generic;
using System.Linq;

// UnionFindTree クラスの定義は前述のものと同じなので省略

class Program
{
    static void Main()
    {
        int N, Q;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            Q = vs[1];
        }

        UnionFindTree uft = new UnionFindTree(N);

        List<string> rets = new List<string>();
        for (int i = 0; i < Q; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int p = vs[0];
            int a = vs[1];
            int b = vs[2];
            if(p == 0)
                uft.Unite(a, b);
            if (p == 1)
            {
                if (uft.IsSame(a, b))
                    rets.Add("Yes");
                else
                    rets.Add("No");
            }
        }
        foreach(string str in rets)
            Console.WriteLine(str);
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

// UnionFindTree クラスの定義は前述のものと同じなので省略

class Program

{

static void Main()

{

int N, Q;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

Q = vs[1];

}

UnionFindTree uft = new UnionFindTree(N);

List<string> rets = new List<string>();

for (int i = 0; i < Q; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int p = vs[0];

int a = vs[1];

int b = vs[2];

if(p == 0)

uft.Unite(a, b);

if (p == 1)

{

if (uft.IsSame(a, b))

rets.Add("Yes");

else

rets.Add("No");

}

foreach(string str in rets)

Console.WriteLine(str);

}

応用問題

D – 連結

N 個の都市があり、K 本の道路と L 本の鉄道が都市の間に伸びています。

i 番目の道路は p_i 番目と q_i 番目の都市を双方向に結び、i 番目の鉄道は r_i 番目と s_i 番目の都市を双方向に結びます。異なる道路が同じ 2 つの都市を結ぶことはありません。同様に、異なる鉄道が同じ 2 つの都市を結ぶことはありません。

ある都市から別の都市に何本かの道路を通って到達できるとき、それらの都市は道路で連結しているとします。鉄道についても同様に定めます。

全ての都市について、その都市と道路・鉄道のどちらでも連結している都市の数を求めてください。

入力されるデータ
N K L
p_1 q_1
p_2 q_2
　…
p_K q_K
r_1 s_1
r_2 s_2
　…
r_L s_L
（ただし 2 ≦ N ≦ 2 * 10^5
1 ≦ K, L ≦ 10^5
1 ≦ p_i, q_i, r_i, s_i ≦ N）

各都市が道路と鉄道でそれぞれ連結しているかをUnionFindTreeで調べます。rootを調べれば連結しているのであれば同じ値を返します。

「道路と鉄道の両方で」という条件がついているのでややこしいですが、ここでは都市 i のふたつのrootをペアにしたもの（ここではふたつの値をカンマで結合させているだけの文字列 key）を考えます。

道路・鉄道のどちらでも連結している都市であればそれらの都市の key は同じ文字列となります。この数を数えます。そのために辞書 dic1 を定義します。また都市 i の key をすぐに取得できるように辞書 dic2 も定義します。最後に都市 i の key は dic2 から取得できるので、これをつかって dic1 から値を取得します。これが都市 i と「道路・鉄道のどちらでも連結している都市の数」です。

using System;
using System.Collections.Generic;
using System.Linq;

// UnionFindTree クラスの定義は省略

class Program
{
    static void Main()
    {
        int N, K, L;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            K = vs[1];
            L = vs[2];
        }

        UnionFindTree uft1 = new UnionFindTree(N);
        for (int i = 0; i < K; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int a = vs[0] - 1;
            int b = vs[1] - 1;
            uft1.Unite(a, b);
        }

        UnionFindTree uft2 = new UnionFindTree(N);
        for (int i = 0; i < L; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int a = vs[0] - 1;
            int b = vs[1] - 1;
            uft2.Unite(a, b);
        }

        int[] ar = new int[N];
        for (int i = 0; i < N; i++)
            ar[i] = uft1.GetRoot(i);
        int[] br = new int[N];
        for (int i = 0; i < N; i++)
            br[i] = uft2.GetRoot(i);

        // (ar[i] br[i]) が同じならそれらは道路・鉄道の両方で連結している
        // 同じ (ar[i] br[i]) を持つ都市の個数を数える
        Dictionary<string, int> dic1 = new Dictionary<string, int>();
        Dictionary<int, string> dic2 = new Dictionary<int, string>();

        for (int i = 0; i < N; i++)
        {
            string str = ar[i] + "," + br[i];
            if(!dic1.ContainsKey(str))
                dic1.Add(str, 1);
            else
                dic1[str]++;
            dic2[i] = str;
        }

        List<int> rets = new List<int>();
        for (int i = 0; i < N; i++)
        {
            string key = dic2[i];
            rets.Add(dic1[key]);
        }

        Console.WriteLine(string.Join(" ", rets));
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

// UnionFindTree クラスの定義は省略

class Program

{

static void Main()

{

int N, K, L;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

K = vs[1];

L = vs[2];

}

UnionFindTree uft1 = new UnionFindTree(N);

for (int i = 0; i < K; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int a = vs[0] - 1;

int b = vs[1] - 1;

uft1.Unite(a, b);

}

UnionFindTree uft2 = new UnionFindTree(N);

for (int i = 0; i < L; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int a = vs[0] - 1;

int b = vs[1] - 1;

uft2.Unite(a, b);

}

int[] ar = new int[N];

for (int i = 0; i < N; i++)

ar[i] = uft1.GetRoot(i);

int[] br = new int[N];

for (int i = 0; i < N; i++)

br[i] = uft2.GetRoot(i);

// (ar[i] br[i]) が同じならそれらは道路・鉄道の両方で連結している

// 同じ (ar[i] br[i]) を持つ都市の個数を数える

Dictionary<string, int> dic1 = new Dictionary<string, int>();

Dictionary<int, string> dic2 = new Dictionary<int, string>();

for (int i = 0; i < N; i++)

{

string str = ar[i] + "," + br[i];

if(!dic1.ContainsKey(str))

dic1.Add(str, 1);

else

dic1[str]++;

dic2[i] = str;

}

List<int> rets = new List<int>();

for (int i = 0; i < N; i++)

{

string key = dic2[i];

rets.Add(dic1[key]);

}

Console.WriteLine(string.Join(" ", rets));

}

D – Equals

1 から N までの整数を並び替えた順列 p_1, p_2, …, p_N があります。また 1 以上 N 以下の整数のペアが M 個与えられます。これらは (x_1 ,y_1), (x_2 ,y_2), …, (x_M ,y_M) で表されます。シカの AtCoDeer くんは順列 p に次の操作を好きなだけ行って、 p_i = i となる i (1 ≦ i ≦ N) の数を最大にしようと考えています。

操作： 1 ≦ j ≦ M なる j を選び、順列 p の x_j 番目と y_j 番目を入れ替える

操作後の p_i = i となる i の数として考えうる最大値を求めてください。

入力されるデータ
N M
p_1 p_2 … p_N
x_1 y_1
x_2 y_2
…
x_M y_M
（ただし p は 1 から N までの整数を並び替えた順列
2 ≦ N ≦ 10^5, 1 ≦ M ≦ 10^5, 1 ≦ x_i, y_i ≦ N）

解説によると、「aとbがスワップ可能、かつ、bとcがスワップ可能であれば、aとcはスワップ可能」。なので「スワップ可能なペアをたどっていける場合は好きな順番にできる」とのこと。

あとは p_i = iとできる個数を数えていくだけです。Union-Find 木応用問題として考えるなら、それぞれの i について、GetRoot(P[i]) == uft.GetRoot(i))であるものの個数を数えるだけです（配列の数字が0ではなく1で始めるので、実際には GetRoot(P[i] – 1) == uft.GetRoot(i))であるものを数える）。

using System;
using System.Collections.Generic;
using System.Linq;

// UnionFindTree クラスの定義は省略

class Program
{
    static void Main()
    {
        int N, M;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            M = vs[1];
        }
        int[] P = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

        UnionFindTree uft = new UnionFindTree(N);
        for (int i = 0; i < M; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int a = vs[0] - 1;
            int b = vs[1] - 1;
            uft.Unite(a, b);
        }

        int ans = 0;
        for (int i = 0; i < N; i++)
        {
            // P[i]-1 を i番目に持ってこれるか？
            if (uft.GetRoot(P[i]-1) == uft.GetRoot(i))
                ans++;
        }
        Console.WriteLine(ans);
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

// UnionFindTree クラスの定義は省略

class Program

{

static void Main()

{

int N, M;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

M = vs[1];

}

int[] P = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

UnionFindTree uft = new UnionFindTree(N);

for (int i = 0; i < M; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int a = vs[0] - 1;

int b = vs[1] - 1;

uft.Unite(a, b);

}

int ans = 0;

for (int i = 0; i < N; i++)

{

// P[i]-1 を i番目に持ってこれるか？

if (uft.GetRoot(P[i]-1) == uft.GetRoot(i))

ans++;

}

Console.WriteLine(ans);

}

C – 嘘つきな天使たち

天使の中に悪魔が紛れ込んだ。あなたは上司にこれを報告しなければならないが、上司は『最大でどれだけ悪魔が紛れ込んだか調査しろ』と命じてきた。

「一体、誰が悪魔なんですかね」

あなたが言うと、彼らは『あいつが悪魔だ』と指摘し合った。誰も同じ者を指ささずバラバラの者を指摘していた。どうやら天使は必ず悪魔を、悪魔は必ず天使を指摘しているようだった。『彼ら』はそれぞれ天使か悪魔のどちらかである。

最大で何人の悪魔がいるだろうか。その数を報告してほしい。

入力されるデータ
N
A 1
A 2
…
A N
（ただし 2 ≦ N ≦ 10^5 、
1 ≦ A_i ≦ N
相異なる任意の i, j について A_i ≠ A_j）

問題文には「天使は必ず悪魔を、悪魔は必ず天使を指摘しあっている」とあるので、指摘した者と指摘された者が指摘している者は同類であることになります。ただ指摘するされる関係で全員がつながっているとは限らないので指摘するされる関係でつながったグループがいくつあるのかとその人数を先に考えます。

そこでUnionFindTreeを2つ生成します。ひとつは指摘する者とされる者は同じグループとするUnionFindTree、もうひとつは指摘した者と指摘された者が指摘している者を同一グループとするUnionFindTreeです。

悪魔の人数は、指摘した者と指摘された者が指摘している者を同一グループとしたグループの人数かもしれないし、指摘する者とされる者は同一グループとしたグループの人数からこれを引いたものかもしれません。悪魔として考えられる最大数を求められているので、両者のうち大きい方を採用します。これらの合計が解となります。

using System;
using System.Collections.Generic;
using System.Linq;

// UnionFindTree クラスの定義は省略

class Program
{
    static void Main()
    {
        int N = int.Parse(Console.ReadLine());

        int[] A = new int[N];
        for (int i = 0; i < N; i++)
            A[i] = int.Parse(Console.ReadLine()) - 1;

        // 指摘する者とされる者は同じグループ
        UnionFindTree uft1 = new UnionFindTree(N);

        // 指摘した者と指摘された者が指摘している者は同一グループ
        UnionFindTree uft2 = new UnionFindTree(N);

        for (int i = 0; i < N; i++)
        {
            uft1.Unite(i, A[i]);
            uft2.Unite(i, A[A[i]]);
        }

        // それぞれのrootの個数を数える
        Dictionary<int, int> dic1 = new Dictionary<int, int>();
        Dictionary<int, int> dic2 = new Dictionary<int, int>();

        for (int i = 0; i < N; i++)
        {
            int root1 = uft1.GetRoot(i);
            if (!dic1.ContainsKey(root1))
                dic1.Add(root1, 1);
            else
                dic1[root1]++;

            int root2 = uft2.GetRoot(i);
            if (!dic2.ContainsKey(root2))
                dic2.Add(root2, 1);
            else
                dic2[root2]++;
        }

        // 指摘した者と指摘された者が指摘している者を同一グループとしたグループの人数
        // 指摘する者とされる者は同一グループとしたグループの人数からこれを引いたもの
        // 両者のうち大きい方を採用し、総和を求める
        // ただし片方が 0 になる場合は入力が矛盾しているので -1 とする
        int ans = 0;
        foreach (var pair in dic1.ToList())
        {
            ans += Math.Max(pair.Value - dic2[pair.Key], dic2[pair.Key]);
            if (pair.Value - dic2[pair.Key] == 0 || dic2[pair.Key] == 0)
            {
                ans = -1;
                break;
            }
        }
        Console.WriteLine(ans);
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

// UnionFindTree クラスの定義は省略

class Program

{

static void Main()

{

int N = int.Parse(Console.ReadLine());

int[] A = new int[N];

for (int i = 0; i < N; i++)

A[i] = int.Parse(Console.ReadLine()) - 1;

// 指摘する者とされる者は同じグループ

UnionFindTree uft1 = new UnionFindTree(N);

// 指摘した者と指摘された者が指摘している者は同一グループ

UnionFindTree uft2 = new UnionFindTree(N);

for (int i = 0; i < N; i++)

{

uft1.Unite(i, A[i]);

uft2.Unite(i, A[A[i]]);

}

// それぞれのrootの個数を数える

Dictionary<int, int> dic1 = new Dictionary<int, int>();

Dictionary<int, int> dic2 = new Dictionary<int, int>();

for (int i = 0; i < N; i++)

{

int root1 = uft1.GetRoot(i);

if (!dic1.ContainsKey(root1))

dic1.Add(root1, 1);

else

dic1[root1]++;

int root2 = uft2.GetRoot(i);

if (!dic2.ContainsKey(root2))

dic2.Add(root2, 1);

else

dic2[root2]++;

}

// 指摘した者と指摘された者が指摘している者を同一グループとしたグループの人数

// 指摘する者とされる者は同一グループとしたグループの人数からこれを引いたもの

// 両者のうち大きい方を採用し、総和を求める

// ただし片方が 0 になる場合は入力が矛盾しているので -1 とする

int ans = 0;

foreach (var pair in dic1.ToList())

{

ans += Math.Max(pair.Value - dic2[pair.Key], dic2[pair.Key]);

if (pair.Value - dic2[pair.Key] == 0 || dic2[pair.Key] == 0)

{

ans = -1;

break;

}

Console.WriteLine(ans);

}

012 – Red Painting

H 行 W 列のマス目があり、上から i (1 ≦ i ≦ H) 行目、左から j (1 ≦ j ≦ W) 列目のマスを (i, j) と表します。

最初すべてのマスは白いです。ここで、Q 個のクエリが以下の形式で与えられます。

i (1 ≦ i ≦ Q) 番目のクエリについて：

t_i = 1 のとき
整数 r_i, c_i が与えられる。白いマス (r_i, c_i) が赤色で塗られる。
t_i = 2 のとき
整数 ra_i, ca_i, rb_i, cb_i が与えられる。
マス (ra_i, ca_i) とマス (rb_i, cb_i) が赤色で塗られていて、マス (ra_i, ca_i) からマス (rb_i, cb_i) まで赤色マス上を上下左右に移動することで辿り着けるとき Yes、そうでなければ No と出力する。

入力されるデータ
H W
Q
q_1
q_2
…
q_Q

（ただし、q_i は i 番目のクエリの情報であり、以下の 2 つの形式のどちらかを満たします。
1 r_i c_i
2 ra_i ca_i rb_i cb_i

1 ≦ H, W ≦ 2,000
1 ≦ Q ≦ 100,000 ）

2 つの赤色マスが赤色マスでつながっているかどうかを素早く調べるにはどうすればよいでしょうか？隣り合った赤色マス同士は同じグループに属するようにすれば、離れた位置にある赤色マスが同一グループに属するかどうかでつながっているかどうかがわかります。

タイプ 2 のクエリで同じマスが指定される場合があります。この場合、同じグループであるからという理由で “Yes” と出力してしまうと WA（wrong answer：不正解）となってしまうので注意します。

using System;
using System.Collections.Generic;
using System.Linq;

// UnionFindTree クラスの定義は省略

class Program
{
    static void Main()
    {
        int H, W;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            H = vs[0];
            W = vs[1];
        }

        int Q = int.Parse(Console.ReadLine());

        UnionFindTree uft = new UnionFindTree(H * W);
        bool[] painted = new bool[H * W]; // 塗られたかどうかのフラグ

        List<string> rets = new List<string>();
        for (int i = 0; i < Q; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int t = vs[0];
            if (t == 1)
            {
                int r = vs[1] - 1;
                int c = vs[2] - 1;
                int cellNumber = r * W + c;
                painted[cellNumber] = true;

                // 上下左右にマスが存在し、塗られているのであれば同じグループにする
                if (r > 0 && painted[(r - 1) * W + c])
                    uft.Unite(cellNumber, (r - 1) * W + c);
                if (r < H - 1 && painted[(r + 1) * W + c])
                    uft.Unite(cellNumber, (r + 1) * W + c);
                if (c > 0 && painted[r * W + c - 1])
                    uft.Unite(cellNumber, r * W + c - 1);
                if (c < W - 1 && painted[r * W + c + 1])
                    uft.Unite(cellNumber, r * W + c + 1);
            }
            if (t == 2)
            {
                int cellNumber1 = (vs[1] - 1) * W + (vs[2] - 1);
                int cellNumber2 = (vs[3] - 1) * W + (vs[4] - 1);

                // 両方とも塗られていて同じグループなら "Yes"
                if (painted[cellNumber1] && painted[cellNumber2] && uft.GetRoot(cellNumber1) == uft.GetRoot(cellNumber2))
                    rets.Add("Yes");
                else
                    rets.Add("No");
            }
        }
        foreach (string ret in rets)
            Console.WriteLine(ret);
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

// UnionFindTree クラスの定義は省略

class Program

{

static void Main()

{

int H, W;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

H = vs[0];

W = vs[1];

}

int Q = int.Parse(Console.ReadLine());

UnionFindTree uft = new UnionFindTree(H * W);

bool[] painted = new bool[H * W]; // 塗られたかどうかのフラグ

List<string> rets = new List<string>();

for (int i = 0; i < Q; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int t = vs[0];

if (t == 1)

{

int r = vs[1] - 1;

int c = vs[2] - 1;

int cellNumber = r * W + c;

painted[cellNumber] = true;

// 上下左右にマスが存在し、塗られているのであれば同じグループにする

if (r > 0 && painted[(r - 1) * W + c])

uft.Unite(cellNumber, (r - 1) * W + c);

if (r < H - 1 && painted[(r + 1) * W + c])

uft.Unite(cellNumber, (r + 1) * W + c);

if (c > 0 && painted[r * W + c - 1])

uft.Unite(cellNumber, r * W + c - 1);

if (c < W - 1 && painted[r * W + c + 1])

uft.Unite(cellNumber, r * W + c + 1);

}

if (t == 2)

{

int cellNumber1 = (vs[1] - 1) * W + (vs[2] - 1);

int cellNumber2 = (vs[3] - 1) * W + (vs[4] - 1);

// 両方とも塗られていて同じグループなら "Yes"

if (painted[cellNumber1] && painted[cellNumber2] && uft.GetRoot(cellNumber1) == uft.GetRoot(cellNumber2))

rets.Add("Yes");

else

rets.Add("No");

}

foreach (string ret in rets)

Console.WriteLine(ret);

}

グラフの連結成分

グラフの連結成分とは、極大で連結な部分グラフのことを意味します。例として、以下のようなグラフでは、連結成分は 4 個となります。

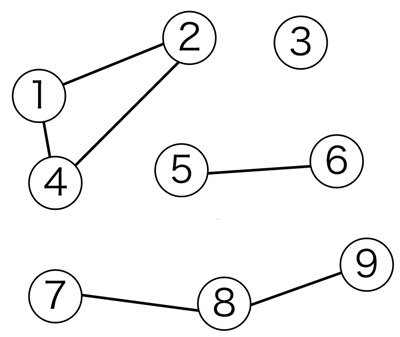
UnionFindTreeで連結している頂点を同じグループにする処理をおこなえば、連結成分の数と各連結成分の頂点数がわかります。

連結成分の大きさ (paizaランク B 相当)

隣接リストと自然数 k が与えられます。このとき、グラフの各連結成分の頂点数が k 以下なら Yes を出力し、そうでなければ No を出力してください。

n k
v_1
a_{1,1} a_{1,2} … a_{1,v_1}
v_2
a_{2,1} … a_{2,v_2}
…
v_n
a_{n,1} … a_{n,v_n}

（ただし、n は頂点の個数を表す整数。k は頂点数の上限を表す自然数
2i 行目：頂点 i に隣接している頂点の個数
2i+1 行目：頂点 i に隣接している頂点の番号が半角スペース区切りで与えられる。

3 ≦ n ≦ 20
2 ≦ k ≦ n – 1 ）

using System;
using System.Collections.Generic;
using System.Linq;

// UnionFindTree クラスの定義は前述のものと同じなので省略

class Program
{
    static void Main()
    {
        int N, K;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            K = vs[1];
        }

        UnionFindTree uft = new UnionFindTree(N);

        for (int i = 0; i < N; i++)
        {
            int a = int.Parse(Console.ReadLine());
            int[] bs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            foreach (int b in bs)
                uft.Unite(i, b - 1);
        }

        int[] parents = new int[N];
        for (int i = 0; i < N; i++)
            parents[i] = uft.GetRoot(i);

        var groups = parents.GroupBy(_ => _);
        _ = groups.Count(); // 連結成分の数

        bool ok = true;
        foreach (var group in groups)
        {
            int cnt = group.Count(); // 各連結成分の頂点数
            if (cnt > K)
            {
                ok = false;
                break;
            }
        }
        if(ok)
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

// UnionFindTree クラスの定義は前述のものと同じなので省略

class Program

{

static void Main()

{

int N, K;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

K = vs[1];

}

UnionFindTree uft = new UnionFindTree(N);

for (int i = 0; i < N; i++)

{

int a = int.Parse(Console.ReadLine());

int[] bs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

foreach (int b in bs)

uft.Unite(i, b - 1);

}

int[] parents = new int[N];

for (int i = 0; i < N; i++)

parents[i] = uft.GetRoot(i);

var groups = parents.GroupBy(_ => _);

_ = groups.Count(); // 連結成分の数

bool ok = true;

foreach (var group in groups)

{

int cnt = group.Count(); // 各連結成分の頂点数

if (cnt > K)

{

ok = false;

break;

}

if(ok)

Console.WriteLine("Yes");

else

Console.WriteLine("No");

}

D – New Friends

1 から N の番号がついた N 人のユーザが利用している SNS があります。

この SNS では 2 人のユーザが互いに友達になれる機能があります。友達関係は双方向的です。すなわち、ユーザ X がユーザ Y の友達であるならば、必ずユーザ Y はユーザ X の友達です。

現在 SNS 上には M 組の友達関係が存在し、i 組目の友達関係はユーザ A_i とユーザ B_i からなります。

以下の操作を行える最大の回数を求めてください。

3 人のユーザ X, Y, Z であって、X と Y は友達、Y と Z は友達であり、X と Z は友達でないようなものを選ぶ。X と Z を友達にする。

入力されるデータ
N M
A_1 B_1
A_2 B_2
…
A_M B_M
（ただし、2 ≦ N ≦ 2×10^5, 0 ≦ M ≦ 2×10^5 )

「X と Y は友達、Y と Z は友達であり、X と Z は友達でないようなものを選ぶ。X と Z を友達にする」とは友達の友達を直接の友達にするという処理のことです。そしてこの処理を繰り返すと間接的な友達はすべて直接の友達になってしまうことに気づきます。それぞれの連結成分が完全グラフ（相違なる 2 つの点が全て隣接している単純グラフ）になるわけです。

つまり、操作がおこなえる回数とは、これらの完全グラフの辺の総数からすでに存在する辺数を差し引いた数です。

完全グラフの辺の総数は頂点数 ×（頂点数 – 1）/ 2 です。各連結成分の頂点数はUnionFindTreeを使えばわかります。

using System;
using System.Collections.Generic;
using System.Linq;

// UnionFindTree クラスの定義は前述のものと同じなので省略

class Program
{
    static void Main()
    {
        int N, M;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            M = vs[1];
        }

        UnionFindTree uft = new UnionFindTree(N);

        for (int i = 0; i < M; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            uft.Unite(vs[0] - 1, vs[1] - 1);
        }

        int[] parents = new int[N];
        for (int i = 0; i < N; i++)
            parents[i] = uft.GetRoot(i);

        long ans = 0;
        var groups = parents.GroupBy(_ => _);
        foreach (var group in groups)
        {
            int cnt = group.Count();
            ans += (long)cnt * (cnt - 1) / 2;
        }
        ans -= M;
        Console.WriteLine(ans);
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

// UnionFindTree クラスの定義は前述のものと同じなので省略

class Program

{

static void Main()

{

int N, M;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

M = vs[1];

}

UnionFindTree uft = new UnionFindTree(N);

for (int i = 0; i < M; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

uft.Unite(vs[0] - 1, vs[1] - 1);

}

int[] parents = new int[N];

for (int i = 0; i < N; i++)

parents[i] = uft.GetRoot(i);

long ans = 0;

var groups = parents.GroupBy(_ => _);

foreach (var group in groups)

{

int cnt = group.Count();

ans += (long)cnt * (cnt - 1) / 2;

}

ans -= M;

Console.WriteLine(ans);

}

データ構造 Union-Find 木蟻本読書会

UnionFindTreeクラスを定義する

UnionFindTreeクラスを使ってみる

応用問題

D – 連結

D – Equals

C – 嘘つきな天使たち

012 – Red Painting

グラフの連結成分

D – New Friends

関連記事

鳩でも分かるC#管理人からのお願い

コメントについて

管理人のモチベーションアップのために

コメントをどうぞ