ひとりで勝手にはじめた蟻本読書会 データ構造 Union-Find 木 蟻本読書会の続きです。
Contents
グラフと二部グラフ
グラフとは、ノード(頂点)群とノード間の連結関係を表すエッジ(枝)群で構成されるデータ構造です。
鉄道や路線バス等の路線図では、駅がどのように路線で結ばれているかが問題となり、線路が具体的にどのような曲線を描いているかは問題とはならないことが多いです。路線図の利用者にとっては、駅と駅の「つながり方」が主に重要な情報となります。
また電気回路の回路図も実際のリード線どおりの形状に図が描かれることはなく「接点がどうつながっているか」だけが問題となります。
このような「つながり方」に着目して抽象化された「点とそれらをむすぶ線」の概念がグラフであり、グラフがもつ様々な性質を探求するのがグラフ理論です。
グラフの辺には方向があるものとないものがあります。方向があるものを有向グラフ、そうではないものを無向グラフといいます。
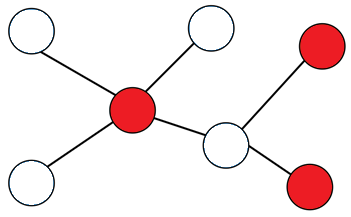
頂点集合を2つに分割して各部分の頂点は互いに隣接しないようにできるグラフのことを2部グラフといいます。辺を共有する頂点を異なる色で塗ることを頂点彩色といいますが、2部グラフであれば2色あれば彩色が可能です。
基本問題
多重辺・自己ループのない無向グラフを構成する 1 ? N の番号がつけられた頂点とそれらを結ぶ M 本の辺の情報が与えられるので、このグラフが二部グラフかを判定してください。
入力されるデータ
N M
a_1 b_1
…
a_M b_M
(ただし 1 ≦ N ≦ 5000, 1 ≦ M ≦ min(N*(N-1)/2, 100,000)
1 ≦ a_i, b_i ≦ N
a_i ≠ b_i )
色は 1 または -1 とします。0 は色がついていない状態です。
最初に見つかった色がついていない頂点に 1 をつけ、あとは色がついていない隣の頂点に -1倍した色をつけます。途中で色に矛盾が生じた場合は2部グラフではないので false を返します。
連結している頂点すべてに色をつけることができたら別の色がついていない頂点を探します(問題文に「このグラフは連結グラフである」とは書いていないことに注意!)。false を返すことなく最後まで処理がおこなわれたら true を返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N, M; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; M = vs[1]; } List<int>[] list = new List<int>[N]; for (int i = 0; i < N; i++) list[i] = new List<int>(); for (int i = 0; i < M; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int a = vs[0] -1; int b = vs[1] - 1; list[a].Add(b); list[b].Add(a); } if (IsBipartiteGraph(N, list)) Console.WriteLine("Yes"); else Console.WriteLine("No"); } static bool IsBipartiteGraph(int n, List<int>[] list) { int[] colors = new int[n]; Queue<int> q = new Queue<int>(); for (int i = 0; i < n; i++) { if(colors[i] != 0) continue; int start = i; q.Enqueue(start); colors[start] = 1; while (q.Count > 0) { int v = q.Dequeue(); int color = colors[v]; foreach (int next in list[v]) { int nextColor = color == 1 ? -1 : 1; if (colors[next] != 0 && colors[next] != nextColor) return false; if (colors[next] == 0) { colors[next] = nextColor; q.Enqueue(next); } } } } return true; } } |
応用問題
N 頂点の木があります。 この木の i 番目の辺は頂点 u_i と頂点 v_i を結んでおり、その長さは w_i です。 あなたは以下の条件を満たすように、この木の頂点を白と黒の 2 色で塗り分けたいです (すべての頂点を同じ色で塗っても構いません)。
同じ色に塗られた任意の 2 頂点について、その距離が偶数である。
条件を満たす塗り分け方を 1 つ見つけて出力してください。この問題の制約下では、そのような塗り分け方が必ず 1 つは存在することが証明できます。
入力されるデータ
N
u_1 v_1 w_1
u_2 v_2 w_2
…
u_N-1 v_N-1 w_N-1
(ただし 1 ≦ N ≦ 10^5
1 ≦ u_i, v_i ≦ N
1 ≦ w_i ≦ 10^9)
辺の長さが偶数なら2つの頂点は同じ色で着色し、辺の長さが奇数なら2つの頂点は異なる色で着色するだけでOK。木なのでこのグラフは連結グラフです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N = int.Parse(Console.ReadLine()); List<int>[] list = new List<int>[N]; for (int i = 0; i < N; i++) list[i] = new List<int>(); List<int>[] ws = new List<int>[N]; for (int i = 0; i < N; i++) ws[i] = new List<int>(); for (int i = 0; i < N - 1; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int u = vs[0] - 1; int v = vs[1] - 1; int w = vs[2]; list[u].Add(v); ws[u].Add(w); list[v].Add(u); ws[v].Add(w); } int[] rets = GetColors(N, list, ws); // -1 と 1 でできた配列が返されるので 0 と 1 に変換 foreach (int i in rets) { if(i == 1) Console.WriteLine(1); else Console.WriteLine(0); } } static int[] GetColors(int n, List<int>[] list, List<int>[] ws) { int[] colors = new int[n]; Queue<int> q = new Queue<int>(); // 木なので連結グラフ。頂点 0 から連結している順に処理していくだけでOK q.Enqueue(0); colors[0] = 1; while (q.Count > 0) { int v = q.Dequeue(); int color = colors[v]; for (int i = 0; i < list[v].Count; i++) { int next = list[v][i]; int nextColor = ws[v][i] % 2 == 0 ? color : -color; if (colors[next] == 0) { colors[next] = nextColor; q.Enqueue(next); } } } return colors; } } |
りんごさんは N 頂点 の連結な無向グラフを持っています。 このグラフにはすでに M 本の辺があり、i 本目の辺は頂点 A i と頂点 B i を繋いでいます。
りんごさんは以下の操作を行うことで、辺を追加しようと思っています。
操作:頂点 u から辺をちょうど 3 本辿ることによって頂点 v に辿り着けるような u, v(u ≠ v) をとり、頂点 u と頂点 v の間に辺を追加する。ただし、すでに頂点 u と頂点 v の間に辺が存在する場合は辺を追加することはできない。
りんごさんが追加できる辺の本数の最大値を求めて下さい。
入力されるデータ
N M
A_1 B_1
A_2 B_2
…
A_M B_M(ただし
多重辺や自己ループは存在しない
与えられるグラフは連結である
2 ≦ N ≦ 10^5
1 ≦ M ≦ 10^5
1 ≦ A_i ,B_i ≦ N )
解説によると、
頂点 s と t の間に奇数長のパスが存在するときは必ず s と t の間に辺が張られる!
なぜなら長さ 4 以上のパスのなかにはパスの長さが 3 になる頂点 s’と t’があり、そこに辺が張られることでその外側にある頂点 s と t のパスの長さも 2 ずつ短くなるからです。頂点 s と t のパスが奇数長であればやがて 3 になって辺が張られることになります。
ではある頂点間に奇数長のパスがどれだけあるかはどうやればわかるでしょうか?
それは「二部グラフであるかどうかに影響される」
二部グラフでないグラフには必ず頂点が奇数個の閉路が存在します。v を奇閉路上のある頂点とします。グラフは連結であるため、任意の頂点の組 (s, t) に対して、s → v → t という順に頂点を訪れるパスが存在します。
もし s → v → t が偶数であった場合、奇閉路上をもう一度辿ることによってパスの長さを奇数にすることができます。
これは二部グラフでないグラフであれば、任意の 2 頂点間に奇数長のパスが存在することになります。そのためグラフが完全グラフになるまで辺を追加することができます。したがって追加できる辺の本数の最大値は N * (N – 1) / 2 – M です。
では二部グラフの場合はどうなるでしょうか?
二部グラフであれば頂点を黒と白に塗り分けることができるのですが、同じ色の頂点の間には絶対に辺が張られることはありません。なぜなら同じ色である頂点のパスの長さは必ず偶数長になるからです。この場合は追加できる辺の本数の最大値は B を黒の頂点の個数、W を白の頂点の個数とすると、B * W – M となります。
GetColorsメソッドは2部グラフの各頂点に塗った色として要素が 1 または -1 の配列を返します。2部グラフでない場合は要素がすべて 0 の配列を返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N, M; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; M = vs[1]; } List<int>[] list = new List<int>[N]; for (int i = 0; i < N; i++) list[i] = new List<int>(); for (int i = 0; i < M; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int a = vs[0] - 1; int b = vs[1] - 1; list[a].Add(b); list[b].Add(a); } int[] colors = GetColors(N, list); if (colors[0] != 0) // グラフは2部グラフである { // int型の範囲を超えるので注意! long B = colors.Count(_ => _ == -1); long W = colors.Count(_ => _ == 1); Console.WriteLine(B * W - M); } else { long n = N; Console.WriteLine(n * (n - 1) / 2 - M); } } static int[] GetColors(int n, List<int>[] list) { int[] colors = new int[n]; Queue<int> q = new Queue<int>(); q.Enqueue(0); colors[0] = 1; while (q.Count > 0) { int v = q.Dequeue(); int color = colors[v]; foreach (int next in list[v]) { int nextColor = color == 1 ? -1 : 1; if (colors[next] != 0 && colors[next] != nextColor) return new int[n]; if (colors[next] == 0) { colors[next] = nextColor; q.Enqueue(next); } } } return colors; } } |
