ひとりで勝手にはじめた蟻本読書会 座標圧縮 領域の個数 蟻本読書会 の続きです。
Contents
セグメント木とは?
セグメント木は、固定長配列にいくつかの操作を加えたデータ構造です。セグメント木は、基本的には以下の操作を時間計算量 O(logN) ですることができます。
i 番目の要素に x を代入
i 番目の要素を取得
l 番目の要素から r 番目の要素の最大値、最小値、総和などを計算する
配列のある区間の総和を高速で計算するアルゴリズムに累積和があります。累積和は事前に A[0] から A[i] までの総和である S[0], S[1], … S[N] を計算することで 区間 [a, b] の総和を S[b] – S[a – 1] で計算しようというものです。区間の総和を計算する大量のクエリに高速に対応することができます。
しかし累積和は途中で配列の要素が更新されるとS[0], S[1], … S[N] を再度計算しなおさないといけないので、配列の要素が更新されるクエリがある場合、高速に対応することができません。
セグメント木は「区間に対する処理を、高速に行うデータ構造」です。累積和だとできないような更新と計算の両方が必要なクエリにも対応できます。
データの更新
管理対象となるデータ件数の2倍のサイズの配列で、効率的にデータを管理します。またセグ木は完全二分木です。そのため管理対象のデータ数が 8 だとすると、配列のサイズは その 2 倍である 16 となりますが、9 個だと 32 になります。
扱いたいデータの個数を N としたとき、N ≦ 2^n を満たす 2^n を考えます。この 2^n を 2 倍した数が配列のサイズとなるのです(N = 9 なら 9 ≦ 2^4 = 16 なのでその 2倍の 32 が配列のサイズ)。
管理対象のデータ数が 8 だとすると、配列のサイズは 16 となりますが、管理の対象となるデータは 配列の index 7 に格納します。それよりも前の部分に各区間の値(最大値や総和など)を格納するのです。

この例では 8 個のデータの最大値を管理します。8 個のデータは index 7 ~ 14 に格納されます。 index 0 には全体の最大値、index 1 には index 7 ~ 10 の最大値、index 2 には index 11 ~ 14 の最大値、index 3 には index 7 ~ 8 の最大値、index 4 には index 9 ~ 10 の最大値 … というように格納していきます。データは 0 以上であり、最大値を考えているので最初は 0 が格納されています(最大値であれば int.MaxValue とか臨機応変に)。
データが更新されたらその上に格納されている各区間の最大値も更新します。
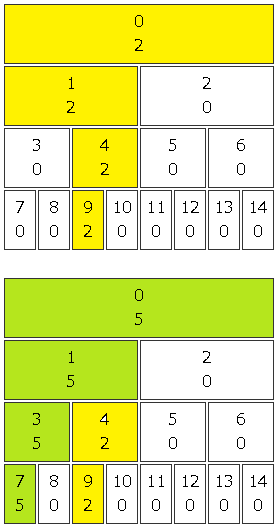
親の index は (子の index – 1) / 2 で切り捨て除算することで求められます。また(親の index * 2 + 1) で左の子の index が、(親の index * 2 + 2) で右の子の index を求めることができます。
そしてセグメント木であれば10万件のデータであったとしても17回で最下層の index から頂点の index 0 にたどり着くことができます。
任意の区間の最大値は?
任意の区間の最大値を知るにはどうすればよいでしょうか? 半開区間 [a,b) の最大値を計算する方法を考えます。
まず上の区間から順番に考えます。一番上の区間とはデータ全体です。任意の区間なので a == 0 かつ b == N でないなら再帰的に以下の操作をおこないます。
考えようとしている区間が、[a,b) に全く含まれないなら、操作に影響しない値(0 とか int.MaxValue など)を返す。
考えようとしている区間が [a,b) に完全に含まれているなら、その値を返す。
どちらでもない場合、2 つの子ノードに対して再帰的に操作をおこなう。
こうすることで区間の最大値を計算量 O(logN) で求めることができるのです。
遅延評価を伴わないセグメントツリー
以下は配列の要素の更新と区間の総和を計算するクエリーに対応する問題です。
B – Fenwick Tree
長さ N の数列 a[0], a[1], …, a[N-1] に Q 個のクエリが飛んできます。処理してください。
0 p x ⇒ a[p] の値を p 増加させる
1 l r ⇒ a[l] から a[r-1] までの総和を出力する入力されるデータ
N Q
a[0] a[1] … a[N-1]
Query 0
Query 1
Query Q-1(ただし、1 ≦ N, Q ≦ 500,000
0 ≦ a[i], x ≦ 10^9 )
タイトルからわかるようにフェニック木をコーディングする問題ですが、セグメント木でも対応できます。
まずセグメント木をクラスで実装します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
using System; using System.Collections.Generic; using System.Linq; class SegTree { int N; long[] Sum = { }; public SegTree(int n) { //完全二分木にするため、データ数を2の倍数にする。 N = 1; while (N < n) N *= 2; Sum = new long[2 * N]; for (int i = 0; i < values.Length; i++) Sum[i + n - 1] = values[i]; for (int i = n - 2; i >= 0; i--) Sum[i] = Sum[i * 2 + 1] + Sum[i * 2 + 2]; } public long GetValue(int index) { return Sum[index + N - 1]; // index 番目の値はここに格納されている } //index番目の値をxに変更する関数 public void Update(int index, long x) { index += N - 1; Sum[index] = x; while (index > 0) { index = (index - 1) / 2; //親のノードのindex Sum[index] = Sum[2 * index + 1] + Sum[2 * index + 2]; } } public long GetSum(int a, int b) { return GetSum(a, b, 0, 0, N); } long GetSum(int a, int b, int index, int left, int right) { if (a >= right || b <= left) return 0; //考えようとしている区間が[a,b)に完全に含まれているなら、その値を返せばよい。 if (a <= left && b >= right) return Sum[index]; //どちらでもない場合、A[index]の2つの子ノードに対して再帰的に操作を行う。 long value1 = GetSum(a, b, 2 * index + 1, left, (left + right) / 2); long value2 = GetSum(a, b, 2 * index + 2, (left + right) / 2, right); return value1 + value2; } } |
定義したSegTreeクラスで解を求めます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class Program { static void Main() { int N, Q; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; Q = vs[1]; } int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); SegTree segTree = new SegTree(A.Length); for (int i = 0; i < A.Length; i++) segTree.Update(i, A[i]); for (int i = 0; i < Q; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); if(vs[0] == 0) { long value = segTree.GetValue(vs[1]); segTree.Update((int)vs[1], value + vs[2]); } if (vs[0] == 1) { long value = segTree.GetSum(vs[1], vs[2]); Console.WriteLine(value); } } return; } } |
遅延評価セグメントツリー
遅延評価とは、値の伝播を遅らせるテクニックです。値の更新が特定の要素だけでなく、区間に対しておこなわれるとき、区間の長さだけ更新処理が必要になりそうですが、この処理にかかる計算量を減らそうというものです。
ここでは遅延評価用の配列を別に用意します。そして遅延評価用の配列では自ノードの区間に一様におこなわれた更新された値を持つことにします。
遅延評価用の配列に値が入っている要素は、どこかのタイミングで遅延配列の情報を実際に値が格納されている配列に伝播させなければいけません。これはどのタイミングでおこなえばよいのでしょうか? それはクエリでそのノードにアクセスしたときです。伝播させる処理は必要に迫られるまで先送りするわけです。
029 – Long Bricks
W 個の正方形のマスが左右に並んだ水平な部分があります。最初、すべての部分について、高さは 0 です。ここに高さ 1 のレンガを N 個、順番に積みます。高さ h の面に接着したレンガの上面の高さは h+1 になります。
i 番目に積むレンガは、左から L_i 番目から R_i 番目のマスをちょうど覆うように置きます。このとき、レンガが覆う範囲の中で最も高い水平な面で接着します。各レンガについて、上面の高さを求めてください。
入力される値
W N
L_1 R_1
L_2 R_2
L_3 R_3L_N R_N
ただし
2 ≦ W ≦ 500,000
1 ≦ N ≦ 250,000
1 ≦ L_i ≦ R_i ≦ W
レンガは以下のような形で置かれていくわけですね。
以下のような入力が与えられた場合は
|
1 2 3 4 5 6 |
18 5 // W N 3 11 // L_1 R_1 7 15 5 9 13 18 3 5 // L_5 R_5 |
レンガは以下のように置かれます。答えは 1,2,3,3,4 となります。
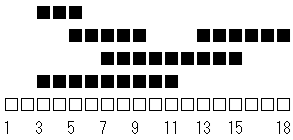
ではどのように考えればよいでしょうか? 最初は閉区間 [3, 11] で高さの最大値を考えます。最初はレンガはひとつも置かれていないので 0 です。レンガを置くことで高さが 1 上昇します。レンガの上面は平らなので閉区間 [3, 11] すべての高さを 1 に変更します。
次は閉区間 [7, 15] で高さの最大値を考えます。この場合、高さの最大値は 1 です。レンガを置くことで高さが 1 上昇します。レンガの上面は平らなので閉区間 [3, 11] の高さはこの最大値に1を加えた 2 にすべて変更されます。
これは指定された区間の最大値の取得と指定された区間の値を更新するという大量のクエリに高速で対応せよという問題です。実は 平方分割で区間を指定した値の更新と最大値の取得という大量のクエリに対応する で同じ問題を扱っています。今回はセグメント木で攻略します。
セグメント木を以下のように定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |
using System; using System.Collections.Generic; using System.Linq; class SegTree { int N; long[] Max = { }; long[] Lazy = { }; public SegTree(int n, long[] values) { N = 1; while (N < n) N *= 2; Max = new long[2 * N]; Lazy = new long[2 * N]; } // index 番目のノードについて遅延評価を行う void Eval(int index, int l, int r) { // 遅延配列が空でない場合、自ノード及び子ノードへの値の伝播が起こる if (Lazy[index] != 0) { Max[index] = Lazy[index]; // 最下段でないなら子に伝搬させる if (r - l > 1) { Lazy[2 * index + 1] = Lazy[index]; Lazy[2 * index + 2] = Lazy[index]; } // 伝播が終わったので、自ノードの遅延配列を空にする Lazy[index] = 0; } } public void Updates(int a, int b, long x) { Updates(a, b, x, 0, 0, N); } void Updates(int a, int b, long value, int index, int left, int right) { // index 番目のノードに対して遅延評価を行う Eval(index, left, right); // 範囲外なら何もしない if (b <= left || right <= a) return; // 完全に被覆しているならば、遅延配列に値を入れた後に評価 // そうでないならば、子ノードの値を再帰的に計算して更新して値を取ってくる if (a <= left && right <= b) { Lazy[index] = value; Eval(index, left, right); } else { Updates(a, b, value, 2 * index + 1, left, (left + right) / 2); Updates(a, b, value, 2 * index + 2, (left + right) / 2, right); Max[index] = Math.Max(Max[2 * index + 1], Max[2 * index + 2]); } } public long GetMax(int a, int b) { return GetMax(a, b, 0, 0, N); } long GetMax(int a, int b, int index, int left, int right) { if (a >= right || b <= left) return 0; // 関数が呼び出されたら評価! eval(index, left, right); //考えようとしている区間が[a,b)に完全に含まれているなら、その値を返せばよい。 if (a <= left && b >= right) return Max[index]; //どちらでもない場合、Max[index]の2つの子ノードに対して再帰的に操作を行う。 long value1 = GetMax(a, b, 2 * index + 1, left, (left + right) / 2); long value2 = GetMax(a, b, 2 * index + 2, (left + right) / 2, right); return Math.Max(value1, value2); } } |
定義したSegTreeクラスを用いて解を求めます。SegTreeクラスのGetMax, Updatesメソッドは半開区間を想定しているので第二引数は right + 1 を渡します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
class Program { static void Main() { int W, N; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); W = vs[0] + 1; N = vs[1]; } long[] A = new long[W]; SegTree segTree = new SegTree(W, A); List<long> rets = new List<long>(); for (int i = 0; i < N; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int left = vs[0] - 1; int right = vs[1] - 1; // 引数は半開区間を想定しているので第二引数は right + 1 を渡す long max = segTree.GetMax(left, right + 1); segTree.Updates(left, right + 1, max + 1); rets.Add(max + 1); } foreach(long ret in rets) Console.WriteLine(ret); } } |
