ふと素数かどうかを判断するメソッドなんてあるのかなと思って検索したけどC#には標準でそのようなものはないらしい。自作するとすればどのようにすればよいか?
簡単な方法
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
bool IsPrime(long value) { // 1や0、負数は素数ではない if(value < 2) return false; // 2と3は素数である if(value == 2 || value == 3) return true; // 4以上の値がわたされたときは3以上の数で割ってみて割りきれる場合は素数ではない // value -1 でも割りきれない場合はループをぬける for(long l=3; l< value; l++) { if(value % l == 0) return false; } // ループから抜けてしまった場合は素数である return true; } |
ただこの方法は無駄な部分が多すぎます。2で割り切れないものなら4とか8でも割り切れません。そこでループ内で割り切れるかどうかチェックするのは奇数だけで充分なはずです。
それから商をしらべて割ろうとしている数よりも小さくなってしまった場合、今後割り切れる数がみつかるとすれば商はそれよりも小さな値になるということになります。ということはもっと早く割り切れる数がみつからないとおかしいということになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
bool IsPrime(long value) { if(value < 2) return false; if(value == 2 || value == 3) return true; // 2以外の偶数であれば素数ではない if(value % 2 == 0) return false; // 奇数だけ調べる for(long l=3; l< value; l += 2) { if(value % l == 0) return false; // これ以上調べても意味なし if(value / l <= l) break; } return true; } |
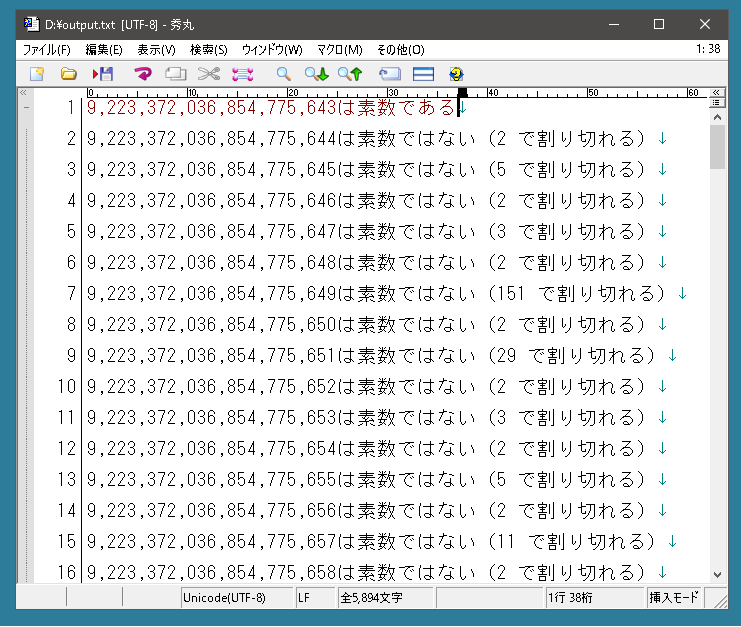
さてlong型で一番大きな値は9,223,372,036,854,775,807です。922京3372兆0368億5477万5807は素数ではありません。ではこれより2小さい値は素数なのかというと違うようです。これよりも小さな値で最大のものは9,223,372,036,854,775,783です。
指定した以上の整数で素数を調べるプログラムを作成しました。時間がかかるので制限もつけます。9,223,372,036,854,775,783が素数であることを調べる処理には1分くらいかかります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
public partial class Form1 : Form { public Form1() { InitializeComponent(); } private void Form1_Load(object sender, EventArgs e) { long value = long.MaxValue; numericUpDown1.Maximum = value; } bool isStop = true; private void button1_Click(object sender, EventArgs e) { isStop = false; Timer timer = new Timer(); timer.Tick += Timer_Tick; timer.Interval = (int)numericUpDown2.Value * 1000; timer.Start(); // 非同期処理にしないとうまくいかない Task.Run(() => { GetPrimesFile(); }); // 時間になったら処理をストップする void Timer_Tick(object sender1, EventArgs e1) { Timer t = (Timer)sender1; t.Stop(); t.Dispose(); isStop = true; } } void GetPrimesFile() { // 実行ファイルと同じフォルダに結果をファイルとして保存する string outputPath = Application.StartupPath + "\\output.txt"; System.IO.StreamWriter sw = new System.IO.StreamWriter(outputPath); long value = (long)numericUpDown1.Value; int i = 0; while(!isStop) { sw.WriteLine(GetPrimeString(value)); // 10000件出力したら時間にならなくても処理を終了する i++; if(i > 10000) break; // 時間になったら処理を終了する if(isStop) break; // longの最大値になったら終了する if(value == long.MaxValue) break; value++; } sw.Close(); // ファイルを開く System.Diagnostics.Process.Start(outputPath); } string GetPrimeString(long value) { if(value < 2) return value.ToString("#,0") + "は素数ではない"; if(value == 2 || value == 3) return value.ToString("#,0") + "は素数である"; if(value % 2 == 0) return value.ToString("#,0") + "は素数ではない(2 で割り切れる)"; for(long l = 3; l < value; l += 2) { if(isStop) return value.ToString() + "タイムアップ"; if(value % l == 0) return value.ToString("#,0") + "は素数ではない(" + l.ToString("#,0") +" で割り切れる)"; if(value / l <= l) break; } return value.ToString("#,0") + "は素数である"; } } |
1から順番にチェックしていくのであれば1秒あれば10000件は簡単に処理できます。ファイルが大きくなりすぎないように10000件で処理を止めています。
ちなみに9,223,372,036,854,775,784以降の結果はこうなります。
9,223,372,036,854,775,784は素数ではない(2 で割り切れる)
9,223,372,036,854,775,785は素数ではない(3 で割り切れる)
9,223,372,036,854,775,786は素数ではない(2 で割り切れる)
9,223,372,036,854,775,787は素数ではない(13 で割り切れる)
9,223,372,036,854,775,788は素数ではない(2 で割り切れる)
9,223,372,036,854,775,789は素数ではない(11 で割り切れる)
9,223,372,036,854,775,790は素数ではない(2 で割り切れる)
9,223,372,036,854,775,791は素数ではない(3 で割り切れる)
9,223,372,036,854,775,792は素数ではない(2 で割り切れる)
9,223,372,036,854,775,793は素数ではない(7 で割り切れる)
9,223,372,036,854,775,794は素数ではない(2 で割り切れる)
9,223,372,036,854,775,795は素数ではない(5 で割り切れる)
9,223,372,036,854,775,796は素数ではない(2 で割り切れる)
9,223,372,036,854,775,797は素数ではない(3 で割り切れる)
9,223,372,036,854,775,798は素数ではない(2 で割り切れる)
9,223,372,036,854,775,799は素数ではない(17 で割り切れる)
9,223,372,036,854,775,800は素数ではない(2 で割り切れる)
9,223,372,036,854,775,801は素数ではない(157 で割り切れる)
9,223,372,036,854,775,802は素数ではない(2 で割り切れる)
9,223,372,036,854,775,803は素数ではない(3 で割り切れる)
9,223,372,036,854,775,804は素数ではない(2 で割り切れる)
9,223,372,036,854,775,805は素数ではない(5 で割り切れる)
9,223,372,036,854,775,806は素数ではない(2 で割り切れる)
9,223,372,036,854,775,807は素数ではない(7 で割り切れる)
それから9,223,372,036,854,775,783の前の素数は9,223,372,036,854,775,643です。このくらいの数になると100個以上素数ではない自然数が続くことも珍しくありません。また9,223,372,036,854,775,753は素数ではありません。266,416,229 で割り切れます。
あとこんな話もあります。素数が連続して1兆出てこないこともあります。

その数が素数であるか判断するには
例示してあるプログラムで言えば
Int(sqrt(value))までで割り切れなければ素数です。
こうすることで、long型の最大値付近の素数を探す場合
計算が早くなるかもしれません。