ひとりで勝手にはじめた蟻本読書会 巡回セールスマン問題 蟻本読書会 の続きです。
繰り返し2乗法
繰り返し2乗法とは、指数を2の累乗の積に分解し、計算を効率化するテクニックです。3の50乗を1000000007(10^9 + 7)で割った余りを出力せよという問題が出されたときどうすればよいでしょうか? Math.Pow メソッドで計算しようとしてもオーバーフローしてしまうので以下のようなループを使って計算することになります。
|
1 2 3 4 5 6 7 8 9 10 |
long Pow(long x, long n, long mod) { long ans = 1; for(int i = 0; i < n; i++) { ans *= x; ans %= mod; } return ans; } |
これは実際に 3 を 50回かける処理をしているだけです。50回なら回数が少ないのでこれでも構わないのかもしれませんが、以下のような問題の場合はどうなるでしょうか?
069 – Colorful Blocks 2
N 個のブロックが横一列に並んでおり、左から順に 1 から N までの番号が付けられています。
これらのブロックそれぞれを、K 種類の色のうちいずれか一色で塗ることを考えます。ここで「1 ≦ |i – j| ≦ 2 ならば、ブロック i とブロック j に塗られている色は異なる。ただし、使わない色があってもよい」という条件を満たすように塗らなければなりません。
このようなブロックの塗り方が何通りあるかを、10^9 + 7 で割った余りを出力してください。
入力されるデータ
N K
(ただし、1 ≦ N ≦ 10^18, 1 ≦ K ≦ 10^9)
N が 1 のときは色の種類がそのまま解となります。N が 2 以上の場合は、最初の色の選び方は K 通り、次の色の選び方は K – 1 通り、それ以降の色の選び方は K – 2 通りです。なので K * (K – 1) * (K – 2)^(N – 2) が解となります。問題はこれをどうやって計算するかです。N も K も非常に大きな値です。
繰り返し2乗法とは、指数を2の累乗の積に分解し、計算を効率化するテクニックです。
普通の方法だと N 乗を計算するのに、N 回の掛け算が必要です。しかし例えば 8 乗するのであれば実際に 8 回の掛け算をしなくても、N を 2 乗する、その答えを 2 乗する、さらにその答えを 2 乗するという 3 回の掛け算で解を得ることができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
using System; using System.Collections.Generic; using System.Linq; class Program { // a の n 乗を mod で割ったあまりを返す static long ModPow(long a, long n, long mod) { if (n == 0) return 1; // 0乗にも対応する場合 if (n == 1) return a % mod; if (n % 2 == 1) return (a * ModPow(a, n - 1, mod)) % mod; long t = ModPow(a, n / 2, mod); return (t * t) % mod; } static void Main() { long N, K; { long[] vs = Console.ReadLine().Split().Select(_ => long.Parse(_)).ToArray(); N = vs[0]; K = vs[1]; } if (N == 1) { Console.WriteLine(K); return; } long mod = 1000000007; // K * (K - 1) * (K - 2)^(N - 2) long ans = K; ans *= K - 1; ans %= mod; ans *= ModPow(K - 2, N - 2, mod); ans %= mod; Console.WriteLine(ans); } } |
行列累乗
繰り返し2乗法を応用することで、行列の累乗も効率化できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
static long[,] MatrixMultiply(long[,] mat1, long[,] mat2) { // 同じサイズの正方行列が渡されることを想定している int len10 = mat1.GetLength(0); int len11 = mat1.GetLength(1); int len20 = mat2.GetLength(0); int len21 = mat2.GetLength(1); if (len10 != len11 || len20 != len21 || len10 != len20) throw new Exception("計算不可"); int len = len10; long[,] mat = new long[len, len]; for (int row = 0; row < len; row++) { for (int col = 0; col < len; col++) { for (int i = 0; i < len; i++) mat[row, col] += mat1[row, i] * mat2[i, col]; } } return mat; } static long[,] MatrixPow(long[,] mat, int n) { int len0 = mat.GetLength(0); int len1 = mat.GetLength(1); if (len0 != len1) throw new Exception("計算不可"); long[,] ret = new long[len0, len0]; long[,] copy = (long[,])mat.Clone(); for (int i = 0; i < len0; i++) ret[i, i] = 1; while (n > 0) { if ((n & 1) == 1) ret = MatrixMultiply(copy, ret); copy = MatrixMultiply(copy, copy); n = n >> 1; } return ret; } |
フィボナッチ数列
以下はメモ化再帰を用いてフィボナッチ数列の 第 n 項を求めるコードです。この方法では n が大きな値の場合、求めることができません。配列 memo を大きくしても値を順番に計算するため、n が大きな値になるとそれだけ計算に時間がかかります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
long[] memo = new long[10000]; long Calc(long n) { if (n == 0) return 0; else if (n == 1) return 1; if (memo[n] != 0) return memo[n]; memo[n] = (Calc(n - 1) + Calc(n - 2)); return memo[n]; } |
行列はフィボナッチ数列を求めるときにも使えます。
フィボナッチ数列は A[n] = A[n -1] + A[n -2] でした。
A[n] = 1 * A[n – 1] + 1 * A[n – 2]
A[n – 1] = 1 * A[n – 1] + 0 * A[n – 2]
行列を使うと以下のように変形できます。行列の n 乗部分は上で定義した MatrixPow を使えば高速で計算可能です。
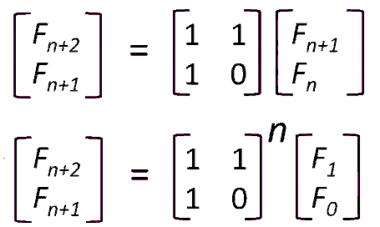
フィボナッチ数列の第 10000 項を計算してみました。普通にやるとオーバーフローするので、BigInteger型(System.Numericsを参照に追加する必要がある)を使っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
class Program { static BigInteger[,] MatrixMultiply(BigInteger[,] mat1, BigInteger[,] mat2) { int len = mat1.GetLength(0); BigInteger[,] mat = new BigInteger[len, len]; for (int row = 0; row < len; row++) { for (int col = 0; col < len; col++) { for (int i = 0; i < len; i++) mat[row, col] += (mat1[row, i] * mat2[i, col]); } } return mat; } static BigInteger[] MatrixMultiply(BigInteger[,] mat, BigInteger[] vec) { int len = mat.GetLength(0); BigInteger[] ret = new BigInteger[len]; for (int row = 0; row < len; row++) { for (int i = 0; i < len; i++) ret[row] += (mat[row, i] * vec[i]); } return ret; } static BigInteger[,] MatrixPow(BigInteger[,] mat, int n) { int len0 = mat.GetLength(0); BigInteger[,] ret = new BigInteger[len0, len0]; BigInteger[,] copy = (BigInteger[,])mat.Clone(); for (int i = 0; i < len0; i++) ret[i, i] = 1; while (n > 0) { if ((n & 1) == 1) ret = MatrixMultiply(copy, ret); copy = MatrixMultiply(copy, copy); n = n >> 1; } return ret; } long Fibo(int n) { long[,] mat = { {1, 1}, {1, 0}, }; mat = MatrixPow(mat, n); return mat[1, 0]; } static void Main() { Console.WriteLine(Fibo(10000)); } } |
フィボナッチ数列第 10000 項の出力結果
第 10000 項は以下のとおり。
33644764876431783266621612005107543310302148460680063906564769974680081442166662368155595513633734025582065332680836159373734790483865268263040892463056431887354544369559827491606602099884183933864652731300088830269235673613135117579297437854413752130520504347701602264758318906527890855154366159582987279682987510631200575428783453215515103870818298969791613127856265033195487140214287532698187962046936097879900350962302291026368131493195275630227837628441540360584402572114334961180023091208287046088923962328835461505776583271252546093591128203925285393434620904245248929403901706233888991085841065183173360437470737908552631764325733993712871937587746897479926305837065742830161637408969178426378624212835258112820516370298089332099905707920064367426202389783111470054074998459250360633560933883831923386783056136435351892133279732908133732642652633989763922723407882928177953580570993691049175470808931841056146322338217465637321248226383092103297701648054726243842374862411453093812206564914032751086643394517512161526545361333111314042436854805106765843493523836959653428071768775328348234345557366719731392746273629108210679280784718035329131176778924659089938635459327894523777674406192240337638674004021330343297496902028328145933418826817683893072003634795623117103101291953169794607632737589253530772552375943788434504067715555779056450443016640119462580972216729758615026968443146952034614932291105970676243268515992834709891284706740862008587135016260312071903172086094081298321581077282076353186624611278245537208532365305775956430072517744315051539600905168603220349163222640885248852433158051534849622434848299380905070483482449327453732624567755879089187190803662058009594743150052402532709746995318770724376825907419939632265984147498193609285223945039707165443156421328157688908058783183404917434556270520223564846495196112460268313970975069382648706613264507665074611512677522748621598642530711298441182622661057163515069260029861704945425047491378115154139941550671256271197133252763631939606902895650288268608362241082050562430701794976171121233066073310059947366875
