ワーシャルフロイド法とは?
ワーシャルフロイド法は最短経路問題で使われるアルゴリズムの1つです。重みが負の辺があっても負閉路がない限り使えます。
下のようになっている場合、0 → 1 と直接移動する場合は 10 ですが、2を経由して 0 → 2 → 1 と移動すると 3 で移動することができます。では任意の頂点から別の任意の頂点へ移動する場合の最短経路はどうなっているでしょうか?
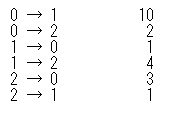
ワーシャルフロイド法のアルゴリズムは以下のとおり。
3つの頂点 (始点、経由点、終点) を選んで距離を計算する。
現在の (始点 → 終点) の最短距離より短ければ、これを (始点 → 終点) の最短距離とする。
これをすべての頂点で計算する。
繰り返すことで最短経路を求めます。
WarshallFloydクラスの定義
ワーシャルフロイド法で最短経路を求めるためのWarshallFloydクラスを定義します。
コンストラクタで頂点数を保存するとともに隣接行列を用意します。また最短経路を求めるために、最短経路で終点の 1 つ前に訪れた頂点を記録する二次元配列も用意します。この配列には頂点 i から頂点 j までの最短経路が (i → … → k → j) の場合、i 行目 j 列目に jの直前に訪れた k を記録されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
using System; using System.Collections.Generic; using System.Linq; public class WarshallFloyd { int[,] _aMat;// 隣接行列 int[,] _pMat;// どこから来たか int _verticesCount = 0; public WarshallFloyd(int verticesCount) { _verticesCount = verticesCount; // 隣接行列(adjacency matrix)をつくる _aMat = new int[verticesCount, verticesCount]; _pMat = new int[verticesCount, verticesCount]; for (int row = 0; row < verticesCount; row++) { for (int col = 0; col < verticesCount; col++) { if (row == col) _aMat[row, col] = 0; else _aMat[row, col] = int.MaxValue; } } for (int row = 0; row < verticesCount; row++) { for (int col = 0; col < verticesCount; col++) _pMat[row, col] = -1; } } } |
ShowAdjacencyMatrixメソッドはデバッグ用です。二次元配列 _aMat と _pMat に格納されている値を表示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
public class WarshallFloyd { public void ShowAdjacencyMatrix() { Console.WriteLine("(aMat)"); for (int row = 0; row < _verticesCount; row++) { List<int> ints = new List<int>(); for (int col = 0; col < _verticesCount; col++) ints.Add(_aMat[row, col]); Console.WriteLine(string.Join(",\t", ints)); } Console.WriteLine(); Console.WriteLine("(pMat)"); for (int row = 0; row < _verticesCount; row++) { List<int> ints = new List<int>(); for (int col = 0; col < _verticesCount; col++) ints.Add(_pMat[row, col]); Console.WriteLine(string.Join(",\t", ints)); } Console.WriteLine(); } } |
SetEdgeメソッドは入力された辺の情報を二次元配列に格納します。
|
1 2 3 4 5 6 7 8 |
public class WarshallFloyd { public void SetEdge(int from, int to, int weight) { _aMat[from, to] = weight; _pMat[from, to] = from; } } |
メインの部分であるGetSolutionメソッドを示します。ここでは 3つの頂点(始点、経由点、終点) を選んで、(始点 → 経由点 → 終点) の最短距離が現在の(始点 → 終点) の最短距離より短ければ、その距離を新たに(始点 → 終点) の最短距離とします。
このとき一番外側のループが経由点のループになるようにします。こうすることで 頂点 x を経由する経路の最短距離を調べるとき、x 未満の頂点のみを経由する経路の最短距離は既に確定しているため、最短距離をうまく更新することができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
public class WarshallFloyd { public void GetSolution() { for (int transit = 0; transit < _verticesCount; transit++) { for (int start = 0; start < _verticesCount; start++) { for (int goal = 0; goal < _verticesCount; goal++) { if (_aMat[start, transit] == int.MaxValue || _aMat[transit, goal] == int.MaxValue) continue; if (_aMat[start, goal] > _aMat[start, transit] + _aMat[transit, goal]) { _aMat[start, goal] = _aMat[start, transit] + _aMat[transit, goal]; _pMat[start, goal] = _pMat[transit, goal]; } } } } } } |
GetShortestDistanceメソッドは引数で渡された始点から終点までの最短距離を返します。
|
1 2 3 4 5 6 7 |
public class WarshallFloyd { public int GetShortestDistance(int start, int goal) { return _aMat[start, goal]; } } |
GetShortestPathメソッドは引数で渡された始点から終点までの最短経路を返します。_pMatのstart行を調べれば各列へ移動するために直前にとおる地点の頂点番号が記録されているので、それを終点から始点までたどっていき、逆順にすれば始点から終点までの最短経路を取得することができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
public class WarshallFloyd { public List<int> GetShortestPath(int start, int goal) { List<int> path = new List<int>(); // たどり着けない if(GetShortestDistance(start, goal) == int.MaxValue) return path; path.Add(goal); // 始点と終点が同じ if(start == goal) return path; // 終点から始点へとたどって行く int temp = _pMat[start, goal]; while (temp != start) { path.Add(temp); temp = _pMat[start, temp]; } path.Add(start); path.Reverse(); return path; } } |
実際に最短経路を求めてみることにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
public class Program { static void Main() { WarshallFloyd wf1 = new WarshallFloyd(3); wf1.SetEdge(0, 1, 10); wf1.SetEdge(1, 0, 1); wf1.SetEdge(0, 2, 2); wf1.SetEdge(2, 0, 3); wf1.SetEdge(1, 2, 4); wf1.SetEdge(2, 1, 1); Console.WriteLine("処理前の隣接行列"); wf1.ShowAdjacencyMatrix(); wf1.GetSolution(); Console.WriteLine("処理後の隣接行列"); wf1.ShowAdjacencyMatrix(); for (int start = 0; start < 3; start++) { for (int goal = 0; goal < 3; goal++) { int distance = wf1.GetShortestDistance(start, goal); List<int> path = wf1.GetShortestPath(start, goal); if (distance < int.MaxValue) { Console.WriteLine($"{start} から {goal} への最短距離は {distance}"); Console.WriteLine($"最短経路は {string.Join(" → ", path)}"); } else { Console.WriteLine($"{start} から {goal} へはたどり着けない"); } } } } } |
実行結果は以下のとおり。


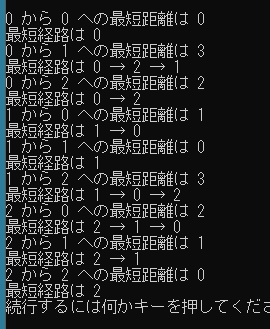
負閉路の検出
負閉路とは、枝の重みの総和が負となる閉路です。一般的に負閉路が存在するグラフでは最短経路問題を解くことはできません。なぜなら負閉路のなかを移動し続けることで何度でも最短距離を更新することができるからです。
たとえば以下の場合に 0 → 1 の最短距離を考えます。

0 → 2 で -20、2 → 0 で -17、0 → 2 で -37、2 → 0 で -34というように直ちに 0 から 1 に向かわないことで最短距離を無限に更新することができてしまうのです。
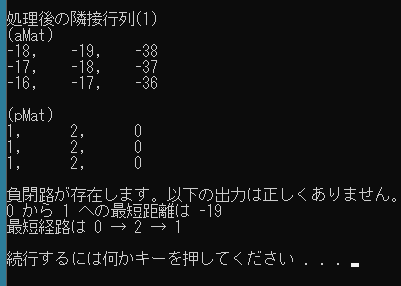
負閉路が存在するグラフでは最短経路問題を解くことはできないのですが、ワーシャルフロイド法は負閉路の存在を検出することができます。
以下のコードを実行します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
public class Program { static void Main() { WarshallFloyd wf1 = new WarshallFloyd(3); wf1.SetEdge(0, 1, 10); wf1.SetEdge(1, 0, 1); wf1.SetEdge(0, 2, -2); wf1.SetEdge(2, 0, 3); wf1.SetEdge(1, 2, 4); wf1.SetEdge(2, 1, 1); wf1.GetSolution(); Console.WriteLine("処理後の隣接行列(1)"); wf1.ShowAdjacencyMatrix(); WarshallFloyd wf2 = new WarshallFloyd(3); wf2.SetEdge(0, 1, 10); wf2.SetEdge(1, 0, 1); wf2.SetEdge(0, 2, -20); wf2.SetEdge(2, 0, 3); wf2.SetEdge(1, 2, 4); wf2.SetEdge(2, 1, 1); wf2.GetSolution(); Console.WriteLine("処理後の隣接行列(2)"); wf2.ShowAdjacencyMatrix(); } } |
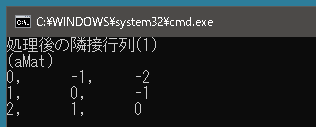
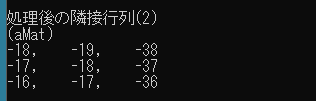
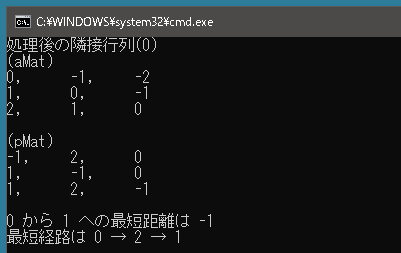
負閉路が存在する場合、隣接行列の対角成分(始点と終点が同じ経路の最短距離)のどれかが負となります(この場合はすべて負になっている)。始点と終点が同じ経路の最短距離を調べることで、与えられたグラフに負閉路が存在するかどうかがわかるのです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
public class WarshallFloyd { public bool CheckNegativeCycle() { for (int i = 0; i < _verticesCount; i++) { if (_aMat[i, i] < 0) return true; } return false; } } public class Program { static void Main() { WarshallFloyd[] wfs = new WarshallFloyd[2]; WarshallFloyd wf1 = new WarshallFloyd(3); wf1.SetEdge(0, 1, 10); wf1.SetEdge(1, 0, 1); wf1.SetEdge(0, 2, -2); wf1.SetEdge(2, 0, 3); wf1.SetEdge(1, 2, 4); wf1.SetEdge(2, 1, 1); wfs[0] = wf1; WarshallFloyd wf2 = new WarshallFloyd(3); wf2.SetEdge(0, 1, 10); wf2.SetEdge(1, 0, 1); wf2.SetEdge(0, 2, -20); wf2.SetEdge(2, 0, 3); wf2.SetEdge(1, 2, 4); wf2.SetEdge(2, 1, 1); wfs[1] = wf2; for (int i = 0; i < wfs.Length; i++) { wfs[i].GetSolution(); Console.WriteLine($"処理後の隣接行列({i})"); wfs[i].ShowAdjacencyMatrix(); if(wfs[i].CheckNegativeCycle()) Console.WriteLine("負閉路が存在します。以下の出力は正しくありません。"); int start = 0; int goal = 1; int distance = wfs[i].GetShortestDistance(start, goal); List<int> path = wfs[i].GetShortestPath(start, goal); Console.WriteLine($"{start} から {goal} への最短距離は {distance}"); Console.WriteLine($"最短経路は {string.Join(" → ", path)}"); Console.WriteLine(); } } } |