トライ木(trie)は有向木の一種で主に文字列を記録するためのデータ構造です。trie という名称は “retrieval”(リトゥリーヴァル。探索、検索)が語源であるため、”tree” と同じ発音を用いますが、ツリー構造との混同を避けるため日本語では「トライ木」という呼ばれます。
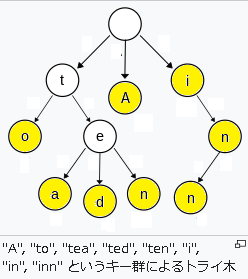
トライ木の特徴として頂点とラベル付き有向辺に文字を割り当てて文字列を記録する方法がとられます。これによってトライ木の根からラベル付き有向辺をたどることで記録された文字列を取り出すことができます。文字列の挿入・検索・削除がすべてO(M)(Mは文字列の長さ)でおこなうことができるのです。そのため辞書のアルゴリズムでも用いられます。
辞書ならC#にはDictionary<TKey,TValue>クラスがあるじゃないか、自作しなくても既存のクラスを使えばよいではないかと言われたらそれまでなのですが、アルゴリズムとしては重要なものだと思うので、ここはあえて車輪の再発明をすることにします。
Nodeクラスの定義
まずNodeクラスを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
public class Node { public Node(char ch) { Ch = ch; } public char Ch = Char.MinValue; // このノードに格納されている文字 public List<Node> ChildNodes = new List<Node>(); // このノードの直下のノード public int UseCount = 0; public bool IsEnd = false; public string Value = ""; } |
IsEndは格納されている文字列がこのノードで終わっていることを示すものです。上の図の黄色いノードに相当する部分です。 “inn”だけでなく”i”や”in”も格納する場合、IsEndは重要な役割をします。IsEnd == trueのときValueも同時に設定することで辞書と同じ機能を持たせることもできます。
UseCountはこのノードを使用している格納されている文字列の数です。文字列を追加したら該当するノードのUseCountをインクリメントし、削除したたデクリメントします。0になったらこのノードは不要ということになります。
Trieクラスの定義
次にTrieクラスを定義します。
|
1 2 3 4 |
public class Trie { Node _root = new Node(Char.MinValue); } |
文字列は存在するか?
まず文字列がTrie木に存在するかを調べるメソッドを定義します。
_rootから順番にノードをたどっていき、最後の文字までたどることができるかを調べます。最後までたどることができない場合は文字列は存在しないことになります。また最後までたどることができても最後のノードのIsEndがtrueでなければやはり探している文字列は存在しないことになります(”ab”を探しているとき”abc”はあるが”ab”はないとか・・)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
public class Trie { public bool Exist(string word) { Node curNode = _root; for (int i = 0; i < word.Length; i++) { Node nextNode = curNode.ChildNodes.FirstOrDefault(nd => nd.Ch == word[i]); if (nextNode != null) curNode = nextNode; else return false; } if (curNode.IsEnd) return true; else return false; } } |
文字列の追加
文字列を追加する処理を示します。
まず文字列がTrie木のなかに存在するか調べます。すでに存在する場合はなにもしません。存在しない場合は_rootから順番にノードをたどっていき、その文字が格納されているノードがあればそのまま使い、ない場合は新しくつくります。どちらの場合も該当するノードのUseCountをインクリメントします。そして最後のノードのIsEndをtrueにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
public class Trie { public Node Insert(string word) { if (Exist(word)) return null; Node curNode = _root; for (int i = 0; i < word.Length; i++) { Node nextNode = curNode.ChildNodes.FirstOrDefault(nd => nd.Ch == word[i]); if (nextNode != null) { curNode = nextNode; } else { Node newNode = new Node(word[i]); // ソートして追加(とりあえず最後に追加してそのあとソートしている。速度的にはあまりいい方法ではない) curNode.ChildNodes.Add(newNode); curNode.ChildNodes = curNode.ChildNodes.OrderBy(_ => _.Ch).ToList(); curNode = newNode; } curNode.UseCount++; } curNode.IsEnd = true; return curNode; } } |
このInsertメソッドは文字列を追加するだけでなく値の設定もおこないます。これによって辞書と同じ機能を持たせることができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
public class Trie { public void Insert(string key, string value) { if (Exist(key)) return; Node node = Insert(key); node.Value = value; } public string GetValue(string key) { Node curNode = _root; for (int i = 0; i < key.Length; i++) { Node nextNode = curNode.ChildNodes.FirstOrDefault(nd => nd.Ch == key[i]); if (nextNode != null) curNode = nextNode; else return ""; } if (curNode.IsEnd) return curNode.Value; else return ""; } } |
文字列を削除する
文字列を削除する場合も最初に文字列がTrie木のなかに存在するか調べます。存在しない場合はなにもしません。
存在する場合は_rootから順番にノードをたどっていき、使用されているノードのUseCountをデクリメントします。もしデクリメントすることで0になったらこのノードとその配下のノードは使われないことを意味するのでそのまま削除してしまいます。
ノードが削除されなかった場合は削除しようとしている文字列を含む別の文字列が存在するということなのでIsEndをfalseにする(Valueもクリアする)だけにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
public class Trie { public void Erase(string word) { if (Exist(word)) { Node curNode = _root; for (int i = 0; i < word.Length; i++) { Node nextNode = curNode.ChildNodes.FirstOrDefault(nd => nd.Ch == word[i]); nextNode.UseCount--; if (nextNode.UseCount == 0) { curNode.ChildNodes.Remove(nextNode); return; } curNode = nextNode; } curNode.IsEnd = false; curNode.Value = ""; } } } |
文字列のソート
Trie木に格納された単語を辞書順に取り出します。ここでは深さ優先探索で文字列を取得しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
public class Trie { public List<string> GetWords() { List<string> words = new List<string>(); string str = ""; dfs(_root, str, words); return words; } void dfs(Node ptr, string str, List<string> word) { if (ptr.IsEnd) word.Add(str); foreach (Node n in ptr.ChildNodes) { str += n.Ch; dfs(n, str, word); str = str.Substring(0, str.Length - 1); } } } |
その他
これだと既存のDictionary<TKey,TValue>クラスを使ったほうがよいです。そこで自由研究として与えられた文字列 T をプレフィックスとして持つ文字列の数を返すメソッドを実装してみることにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
public class Trie { public int CountPrefix(string word) { Node node = GetNode(word, word.Length); if (node != null) return node.UseCount; else return 0; } public Node GetNode(string word, int index) { Node curNode = _root; for (int i = 0; i < index; i++) { Node nextNode = curNode.ChildNodes.FirstOrDefault(nd => nd.Ch == word[i]); if (nextNode != null) curNode = nextNode; else return null; } return curNode; } } |
Trie木に格納された文字列と引数strとの共通プレフィックスのうち最長のものを返すメソッドを実装します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
public class Trie { public string GetLCP(string str) { Node ptr = _root; for (int i = 0; i < str.Length; i++) { Node nextNode = ptr.ChildNodes.FirstOrDefault(nd => nd.Ch == str[i]); if (nextNode != null) ptr = nextNode; else return str.Substring(0, i); } return str; } } |
Trie木に格納された文字列のなかでプレフィックスに引数prefixを含むものを辞書順ですべて返すメソッドを実装します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
public class Trie { public List<string> GetWords(string prefix) { List<string> words = new List<string>(); string str = ""; Node node = GetNode(prefix, prefix.Length); if (node == null) return new List<string>(); dfs(node, str, words); return words.Select(_ => prefix + _).ToList(); } } |
実装したCountPrefixメソッドとGetLCPメソッドとGetWordsメソッドを使ってみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
public class Program { static void Main() { Trie trie = new Trie(); // 3つの文字列をTrie木に追加 trie.Insert("鳩でもわかるC#"); trie.Insert("鳩でもわかるJavaScript"); trie.Insert("鳩には難しすぎるC言語"); // "鳩でもわかる"で始まる文字列は2つあるので2と出力される Console.WriteLine(trie.CountPrefix("鳩でもわかる")); // 3つとも"鳩"で始まる文字列なので出力される Console.WriteLine(trie.CountPrefix("鳩")); // "鳩には難しすぎるC言語"と"鳩には難しすぎるC"まで一致しているので"鳩には難しすぎるC"と出力される Console.WriteLine(trie.GetLCP("鳩には難しすぎるC++")); // "鳩でもわかる"で始まる文字列は"鳩でもわかるC#"と"鳩でもわかるJavaScript"があるので、この2つが出力される List<string> list = trie.GetWords("鳩でもわかる"); foreach (string s in list) Console.WriteLine(s); } } |
