C++でつくったテトリスの完成品

よく動画でテトリスを○分でつくってみたというのがありますが、鳩でもわかるC#管理人はそんなスキルはないので別の領域で勝負するしかありません。「テトリスを○分でつくってみた」はテトリスを完全再現したものではないものがほとんどです。なかでも今回の肝になるスーパーローテーションシステム（SRS）に関しては完全にスルーしているものが多いです。だから私としてはこの部分をキッチリ実装することで他との差別化をしたいのです。

スーパーローテーションシステム（SRS）とは

スーパーローテーションシステム（SRS）とは簡単に説明すると普通に回転させようとすると他のブロックにぶつかって回転できない場合、「回転できない」で終わらせず回転後の位置を平行移動させることで回転させることができるというものです。

またテトリスにはTスピントリプルという大技も存在します。これはSRSを利用して本来なら絶対に入らない場所にTミノをねじ込もうとするテクニックです。SRSがあるとゲームをより面白くすることができるのです。

SRSはテトリスのガイドラインにも組み込まれています。テトリミノがどのような状態のとき、どのように回転軸がずれるのかはガイドラインで決められているのです。やっぱりやるからにはこれに沿ったものを作りたいです。

このあたりをことを解説してくれているのがTetrisちゃんねるです。これまでC#,JavaScriptでテトリスをつくってきましたが、今回もこのサイトを参考にすることにします。

通常の回転処理

まずは通常の回転処理を考えますが、これなら前述のGetInitBlocksRotate33関数やGetInitBlocksRotate44関数を使えばできそうです。そこで最初に普通の方法で回転した場合のテトリミノの各ブロックがどうなるかを考えてみます。これがCanRotate関数です。第一引数は右回転であればTRUE、左回転ならFALSEです。

現在落下中のテトロミノをGetInitBlocksRotate33関数やGetInitBlocksRotate44関数で回転させればよいのですが、回転処理を加えたときの各ブロックのPositionを求める前にm_TetriminoPositionX == 0 m_TetriminoPositionY == 0の状態に戻さなければなりません。そして回転処理を加えたときのブロックのPositionを求めてm_TetriminoPositionX、m_TetriminoPositionY分平行移動されたときのPositionが回転処理後の位置ということになります。

回転処理後のPositionがわかったらあとは当たり判定をするだけです。回転することができるならTRUE、できないならFALSEを返します。最初はこの関数を第二引数、第三引数はともに0を渡して処理をします。これでSRSを適用しないでテトリミノを回転させることができるかの結果が得られます。

テトリミノの回転は可能かを検証する

では実際に回転処理をおこなわせます。Oミノは回転処理をおこないません。回転させても形状が同じだからです。Iミノ以外のテトリミノの処理をRotateRight3関数でおこないます。IミノであればRotateRightI関数でおこないます。

Iミノとそれ以外ではSRS適用下の処理も異なっている

OミノとIミノ以外のテトリミノの回転処理をおこなう関数を示します。最初はCanRotate関数の第二第三引数には0を渡し、SRSは適用されない普通の回転ができないかを調べます。そして回転させることができるのであれば引数付きのRotateRight関数を呼び出して、実際に回転処理をおこないます。

CanRotate関数がFALSEを返した場合はSRS適用下での回転ができないかを調べます。どのようなルールが適用されるかは以下の画像をみてくださし。

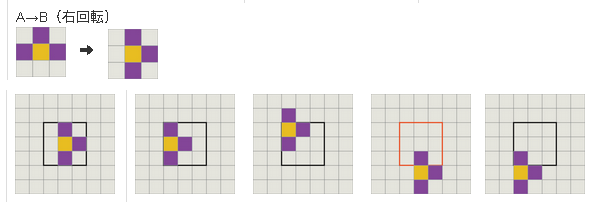
これを見ると通常回転できないのであれば、

回転前の回転角が0度のときは

(1) 左に1マスずらす
(2) 左に1マス、上に1マスずらす
(3) 下に2マスずらす
(4) 左に1マス、下に2マスずらす

この順で調べてみてどれもダメな場合は回転処理はできないということになります。

回転前の回転角が0度以外のときもTetrisちゃんねるに掲載されている図にある順番で回転できるかどうかを調べていきます。

もし回転させたあとテトリミノ全体を平行移動させることで回転できるのであれば、平行移動させるべき値をRotateRightに渡して回転処理をおこないます。

するとOミノとIミノ以外のテトリミノの回転処理をおこなう関数は以下のようなものになります。

回転処理ができる場合のみ回転処理をおこなう

回転処理ができることがわかったら回転処理をおこないます。RotateRight関数の引数はSRS適用下での回転させる場合、どれだけテトリミノを平行移動させるかです。平行移動させるということはメンバ変数であるm_TetriminoPositionXとm_TetriminoPositionYも適切に変更させなければならないことを意味しています。

m_TetriminoAngleとm_TetriminoPositionX、m_TetriminoPositionYを書き換えればあとは描画処理の関数がうまくやってくれます。

左回りも同様に処理する

同様に左回りに対しても行ないます。

これまでテトリミノの生成、描画、移動、回転、消去の処理をおこないました。これだけではあまりにも不十分ですが一応、ゲームとして成り立たせるための最低限のものは実装できたといえます。次回、以降はもう少しゲームらしくすることを追求します。現状、スコアの表示すらできていません。