連続する区間の和
与えられたint型の配列において、長さが 1 以上で総和が与えられた値以下であるものを考えます。そのような区間がいくつあるか、区間の長さで最大のものを求めるにはどうすればいいでしょうか?
(例)int[] a = {4, 5, 6, 8, 2, 6, 7, 4, 2, 15,} 区間の和が15以下のものを対象にするのであれば、
a[0] + a[1] = 9 とか a[1] + a[2] = 11 とか a[0] + a[1] + a[2] = 15 などが対象となります。配列のなかで連続しているもののみが対象です。a[0] + a[1] + a[4] = 11 のように連続していないのであれば和が15以下でも対象とはしません。
最初に left と right を 0 にしておいて a[left + 0] + a[left + 1] + (中略) + a[right] が15以下であるかぎりrightを大きくしていきます。和が15を超えたらleftをひとつ増やして rightはleftの位置に戻します。こうしてleftとrightがしゃくとり虫のように両者の距離を広げたり縮めたりしながら右のほうへ移動していきます。配列上の同じような場所の和を何度も計算するので累積和と組み合わせて使うと処理時間を短縮できるかもしれません。
配列から累積和が格納された配列を求める処理を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static int[] GetPrefixSum(int[] arr) { int[] sum = new int[arr.Length]; for (int i = 0; i < arr.Length; i++) { if (i != 0) sum[i] = arr[i] + sum[i - 1]; else sum[0] = arr[0]; } return sum; } } |
累積和から arr[min] から arr[max]までの和を求める処理を示します。
|
1 2 3 4 5 6 7 8 9 10 |
public class Program { static int GetValue(int[] prefixSum, int min, int max) { if (min != 0) return prefixSum[max] - prefixSum[min - 1]; else return prefixSum[max]; } } |
あとはこれらのメソッドを用いてしゃくとり法で区間の和を計算します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
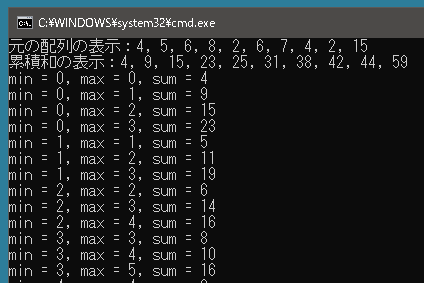
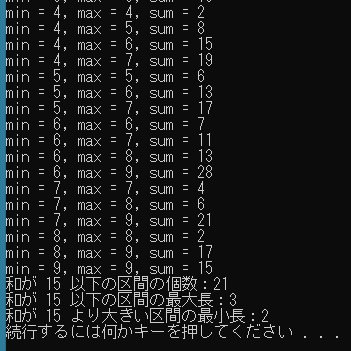
public class Program { static void Main() { int K = 15; int[] arr = { 4, 5, 6, 8, 2, 6, 7, 4, 2, 15, }; Console.WriteLine("元の配列の表示:" + string.Join(", ", arr)); // 累積和を計算する int[] sum = GetPrefixSum(arr); for (int i = 0; i < arr.Length; i++) { if (i != 0) sum[i] = arr[i] + sum[i - 1]; else sum[0] = arr[0]; } Console.WriteLine("累積和の表示:" + string.Join(", ", sum)); // left, right ではその値を含むかどうかがわかりにくいので // その値を含むことが明らかである min, max を使う int min = 0; int max = 0; int count = 0; // 条件を満たす区間は何個存在するか? int maxLength = 0; // 和が15以下の区間の最大長 int minLength = int.MaxValue; // 和が15より大きい区間の最小長 while (true) { int value = GetValue(sum, min, max); // デバッグ用で調べている区間とその和を表示させてみる Console.WriteLine($"min = {min}, max = {max}, sum = {GetValue(sum, min, max)}"); if (value <= K) { // 区間の和が 15 以下なら個数をカウントするとともに // その長さが maxLength より大きければ更新する count++; int length = max - min + 1; if (maxLength < length) maxLength = length; } else { // 区間の和が 15 より大きければ // その長さが minLength より短ければ更新する int length = max - min + 1; if (minLength > length) minLength = length; } if (value <= K) { // 和が15以内であればさらにmax(区間の右側)を 1 大きくする // できない場合は区間の右側は配列の最後まで到達したということなので // 区間の左側を 1 大きくして右側を同じ位置に戻す if (max + 1 < sum.Length) max++; else { min++; max = min; } } else { // 和が15を超えている場合は区間の左側を 1 大きくして右側を同じ位置に戻す min++; max = min; } // max または min は配列の範囲を超えているときは終了 if (max >= sum.Length) break; } // 結果を表示する Console.WriteLine($"和が {K} 以下の区間の個数:{count}"); Console.WriteLine($"和が {K} 以下の区間の最大長:{maxLength}"); Console.WriteLine($"和が {K} より大きい区間の最小長:{minLength}"); } } |
結果は区間の和が15以下の区間は16個、最大長は3、区間の和が15より大きい区間の最短長は2であることがわかりました。
(参考)しゃくとり法の練習問題
単純増加の数え上げ
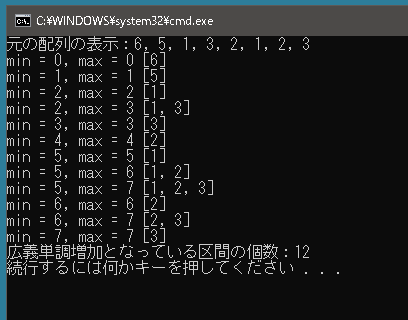
配列内において、連続する部分列のうち広義単調増加となっている区間を数え上げます。広義単調増加とは、a_i ≦ a_(i + 1) (l ≦ i < r) あるか、要素が1つの部分列のことを指します。たとえば int[] a = { 6, 5, 1, 3, 2, 1, 2, 3,} であれば a[5] ~ a[7] だけでなく a[5] ~ a[6]、a[6] ~ a[7]のようなものもカウントします。それから要素が1つの場合も広義単調増加なので a[0] だけ、a[1] だけであっても対象となります。 Showメソッドは、第一引数で渡された配列のなかの、第二引数と第三引数で囲まれた部分の要素をカンマ区切りで表示するためのものです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Show(int[] arr, int min, int max) { int[] ints = new int[max - min + 1]; for (int i = min; i <= max; i++) ints[i - min] = arr[i]; Console.WriteLine($"min = {min}, max = {max} [{string.Join(", ", ints)}]"); } } |
arr[max - 1] と arr[max] を比較すればよいのですが、要素数が1のときは無条件で広義単調増加とみなすので、その場合(min == maxのとき)は別に処理が必要です。それ以外の時は arr[max - 1] ≧ arr[max] であれば広義単純増加なので max をインクリメントし、そうでない場合は min をインクリメントして max に min を代入します。max が最後まで来たら、この場合もmin をインクリメントして max に min を代入します。これで調査対象をすべて調査できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
public class Program { static void Main() { int[] arr = { 6, 5, 1, 3, 2, 1, 2, 3}; Console.WriteLine("元の配列の表示:" + string.Join(", ", arr)); // left, right ではその値を含むかどうかがわかりにくいので // その値を含むことが明らかである min, max を使う int min = 0; int max = 0; int count = 0; // 条件を満たす区間は何個存在するか? while (true) { if (max >= arr.Length) { min++; max = min; if (min >= arr.Length) break; } if (max == min) { // デバッグ用で調べている区間とその和を表示させてみる Show(arr, min, max); count++; max++; } else if (arr[max - 1] <= arr[max]) { // デバッグ用で調べている区間とその和を表示させてみる Show(arr, min, max); count++; max++; } else { min++; max = min; } } Console.WriteLine($"広義単調増加となっている区間の個数:{count}"); } } |
(参考)しゃくとり法の練習問題
同じものが存在しない区間の長さの最大値
問題:さまざまな色の服が一列に並べられて売られています。色は整数で表わされています。ある区間の服をまとめ買いしたいと考えているのですが、同じ色の服は買いたくありません。同じ色が 2 箇所以上存在しない区間のうち、最大の長さを求めよ、という問題が出てきたらどうすれえばいいでしょうか?
min と max をしゃくとり虫のように動かして配列の最後まで調べるのですが、区間内に同じ色の服があるかどうやって調べればよいのでしょうか? 鳩でもわかるC#管理人は辞書の性質を利用しました。
すでに辞書内にあるキーと同じキーでAddメソッドを呼び出すと例外が発生します。もし例外が発生したら重複があるとみなし、辞書内のデータはすべて削除、min をインクリメントします。例外が発生しない場合は区間内に同じ色の服はないので max をインクリメントするとともに 辞書内の要素数が maxLength を超えていたら更新します。max が配列の最後にきた場合も区間内に同じ色があったときと同じ処理をおこないます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
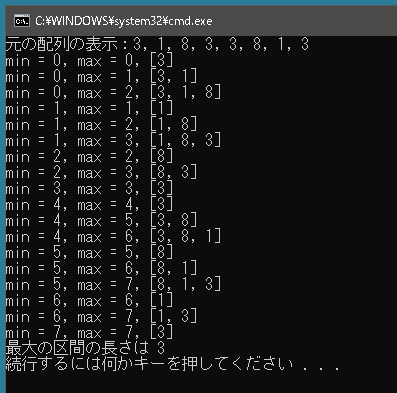
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { int[] arr = { 3, 1, 8, 3, 3, 8, 1, 3 }; Console.WriteLine("元の配列の表示:" + string.Join(", ", arr)); // left, right ではその値を含むかどうかがわかりにくいので // その値を含むことが明らかである min, max を使う int min = 0; int max = 0; Dictionary<int, int> valuePairs = new Dictionary<int, int>(); int maxLength = 0; int curLength = 0; while (true) { if (max >= arr.Length) { valuePairs.Clear(); curLength = 0; min++; max = min; if (min >= arr.Length || max >= arr.Length) break; } try { valuePairs.Add(arr[max], 1); Console.WriteLine($"min = {min}, max = {max}, [{string.Join(", ", valuePairs.Select(_ => _.Key).ToArray())}]"); max++; curLength++; if (maxLength < curLength) maxLength = curLength; } catch { valuePairs.Clear(); curLength = 0; min++; max = min; } } Console.WriteLine("最大の区間の長さは " + maxLength); } } |
(参考)しゃくとり法の練習問題
