点の偏角とは、原点からその点を見たときの方向を角度として表したものです。与えられたいくつかの点を偏角の昇順に並べ替える操作を偏角ソートといいます。
Contents
E – Laser Takahashi
点Aと点Bに挟まれる点の数を求めよという問題です。
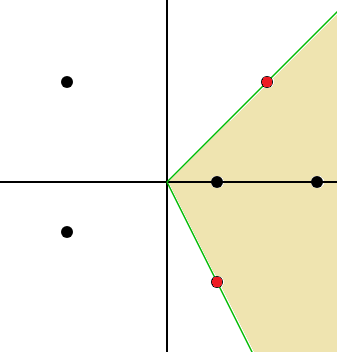
偏角と偏角ソート
この問題では偏角ソートをすることで赤い点で挟まれている点を効率よく数えることができます。
偏角を求めるにはMath.Atan2メソッドを使えばできそうですが、小数による誤差が発生するかもしれません。そこで別の方法を使います。
ソートの比較関数を外積を用いて定義します。ただし、注意点があります。この方法は偏角の差が 180度 未満の時にしか用いることができません。そこで点を上半平面(y > 0 または (y == 0 かつ x > 0))と下半平面(それ以外)にわけます。これで偏角が[0, 180)と[180, 360)のグループにわかれるので、あとはこのなかでソートすればよいです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
class Point { public Point(long x, long y) { X = x; Y = y; } public long X = 0; public long Y = 0; class Comparer : IComparer<Point> { int IComparer<Point>.Compare(Point? a, Point? b) { long v = a.X * b.Y - b.X * a.Y; if (v < 0) return 1; else if (v > 0) return -1; else return 0; } } public static List<Point> DeclinationSort(List<Point> pts, bool descendingOrder) { bool isUpper(Point pt) => pt.Y > 0 || (pt.Y == 0 && pt.X > 0); List<Point> upper = pts.Where(_ => isUpper(_)).OrderBy(_ => _, new Comparer()).ToList(); List<Point> lower = pts.Where(_ => !isUpper(_)).OrderBy(_ => _, new Comparer()).ToList(); List<Point> sorted = upper; sorted.AddRange(lower); if(descendingOrder) sorted.Reverse(); return sorted; } } |
同じ偏角を持つ点が複数ある場合の対処法
偏角ソートしたら点Aの偏角から点Bの偏角で挟まれている点の数を数えればよいのですが、点A, Bと同じ偏角を持つ点が複数あるかもしれないのでそれらを見つける必要があります。
ソートされた点であれば、偏角が同じものがあるとすればその前後です。そこで偏角が同じかどうかを判定するメソッドを定義します。
外積が同じなら2点は同一直線です。ただしこれだけだと原点を挟んでいる(180度ズレている)かもしれないので上下どちらの半平面に属するかも確認します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
class Point { public static bool IsSameDeclination(Point a, Point b) { bool isUpper(Point pt) => pt.Y > 0 || (pt.Y == 0 && pt.X > 0); if (isUpper(a) != isUpper(b)) return false; return a.X * b.Y - b.X * a.Y == 0; } } |
あとは前から順に見ていってIsSameDeclinationがtrueを返したら同じグループにしてしまえばOKです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
class Point { public static List<List<Point>> DeclinationSortGrouping(List<Point> pts, bool descendingOrder) { List<Point> sorted = DeclinationSort(pts, descendingOrder); Stack<List<Point>> stack = new Stack<List<Point>>(); foreach (Point pt in sorted) { if(stack.Count == 0 || !IsSameDeclination(stack.Peek()[0], pt)) stack.Push(new List<Point>()); stack.Peek().Add(pt); } List<List<Point>> rets = stack.ToList(); rets.Reverse(); return rets; } } |
提出コード
実際に提出してAC(正解)したコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
class Program { static void Main() { (int a, int b) ReadInt2() { string[] vs = Console.ReadLine().Split(); return (int.Parse(vs[0]), int.Parse(vs[1])); } (int N, int Q) = ReadInt2(); List<Point> P = new List<Point>(); for (int i = 0; i < N; i++) { (int x, int y) = ReadInt2(); P.Add(new Point(x, y)); } // 偏角ソート(時計回りなので降順にする)して同じ偏角なら同一グループにする var sortedGroups = Point.DeclinationSortGrouping(P, true); int gCount = sortedGroups.Count; // 各グループに属する点の個数 int[] counts = new int[gCount]; // 同じ偏角の点の個数 // 辞書から各点がどのグループに属するかをすばやく取得できるようにする Dictionary<Point, int> pointToGroup = new Dictionary<Point, int>(); for (int i = 0; i < gCount; i++) { counts[i] = sortedGroups[i].Count; var group = sortedGroups[i]; foreach (var p in group) pointToGroup.Add(p, i); } // 累積和をつかってグループAからグループBまでの総和を素早く計算できるようにする // 環状にならんでいるので2周する int[] sums = new int[gCount * 2 + 1]; for (int i = 0; i < gCount; i++) sums[i + 1] = sums[i] + counts[i]; for (int i = 0; i < gCount; i++) sums[i + gCount + 1] = sums[i + gCount] + counts[i]; for (int i = 0; i < Q; i++) { (int a, int b) = ReadInt2(); a--; // 入力は 1-indexed なので・・・ b--; int ga = pointToGroup[P[a]]; // 指定された点が属するグループの添字 int gb = pointToGroup[P[b]]; // 時計回りに回転するので gb < ga のときは [ga, gb + gCount] の総和を求める if (gb < ga) gb += gCount; int ans = sums[gb + 1] - sums[ga]; Console.WriteLine(ans); } } } |
009 – Three Point Angle(★6)
ある方から課題をいただいているのでこれも片付けておきます。
3つの点を選んでできる角の角度の最大値を度数法で出力せよという問題です。相対誤差または絶対誤差が 10^-7 なら正解として扱われます。
これも偏角ソートすればなんとかなりそうです。また角度は誤差がある程度は許容されるのでMath.Atan2を使って問題なさそうです。
3点からできる角は中心とその他の2つにわけて考える
3点からできる角は中心とその他の2つにわけて考えるとうまくいく場合が多いです。
まず中心になる点を選びます。この点が原点になるように全体を平行移動させます。中心になる点を O、残りの2点を A, B、X軸にあるX座標が正になる任意の点を C とすると ∠AOC – ∠BOC が180度に近くなるものを探せばよいことになります。
まず中心の点以外のすべての点の偏角を求めます。それぞれに対してこれに180度を足したものが一番近い別の偏角を探します。このとき二分探索法が使えます。
ある点の偏角に180度を足したものが一番近い別の偏角を探すのに二分探索法を使うと時間計算量は O(logN)、これをすべての点についておこなうので O(NlogN)、中心になる点は全部でNとおりあるのでこれをN回おこなうことになるので全体の時間計算量は O(N×N×logN)となります。N は最大2,000なのでこれなら充分間に合います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 |
class Program { static void Main() { (int a, int b) ReadInt2() { string[] vs = Console.ReadLine().Split(); return (int.Parse(vs[0]), int.Parse(vs[1])); } // 偏角を度数法で求める double Degree(Point pt) { double rad = Math.Atan2(pt.Y, pt.X); double deg = rad / Math.PI * 180; if (deg < 0) deg += 360; return deg; } // 二分探索法でもちいるメソッド int BinarySearch(int ok, int ng, Predicate<int> Ok) { while (Math.Abs(ok - ng) > 1) { var m = (ok + ng) >> 1; if (Ok(m)) ok = m; else ng = m; } return ok; } int N = int.Parse(Console.ReadLine()); List<Point> P = new List<Point>(); for (int i = 0; i < N; i++) { (int x, int y) = ReadInt2(); P.Add(new Point(x, y)); } double ans = 0; for (int a = 0; a < N; a++) { Point center = P[a]; // 点 a が原点にくるように全体を平行移動させた場合の各点の偏角を求める List<double> degs = new List<double>(); for (int b = 0; b < N; b++) { if (a != b) { Point pt = new Point(P[b].X - center.X, P[b].Y - center.Y); double deg = Degree(pt); degs.Add(deg); } } ans = Math.Max(ans, Solve(degs)); // Solve(degs)で点 a が中心のときの最大角がわかる } Console.WriteLine(ans); double Solve(List<double> degs) { double ans = 0; // 偏角をソートし、2周分リストに格納する List<double> sorted1 = degs.OrderBy(_ => _).ToList(); List<double> sorted2 = sorted1.Select(_ => _ + 360).ToList(); List<double> sorted = new List<double>(sorted1); sorted.AddRange(sorted2); int n = sorted.Count; foreach (double d in sorted) { if (d >= 180) break; // 最初の1周分について、180を足したときのもっとも近い値を調べる int ok = n; int ng = -1; int idx = BinarySearch(ok, ng, mid => sorted[mid] >= d + 180); // d + 180 以上のもっとも近い偏角の値 if (idx < n) { double ans0 = d - sorted[idx]; // 偏角の差が 0以上180以下になるように調整する if (ans0 < 0) ans0 += 360; if(ans0 > 180) ans0 = 360 - ans0; ans = Math.Max(ans, ans0); } // d + 180 未満のもっとも近い偏角の値 if (idx - 1 >= 0) { double ans0 = d - sorted[idx - 1]; if (ans0 < 0) ans0 += 360; if (ans0 > 180) ans0 = 360 - ans0; ans = Math.Max(ans, ans0); } } return ans; } } } |
