今回は平衡二分探索木のひとつである赤黒木を実装します。
Contents
赤黒木とは?
赤黒木は平衡二分探索木のひとつです。赤黒木は以下のような特徴をもっています。
二分探索木である以上、ノードの左側の子はそのノードがもつ値より小さく、右の子はその値以上である。
ノードは赤と黒いずれかの色を持つ
根は必ず黒である。
「ノードの黒深さ」を根からそのノードまでの黒ノードの数と定義する。
根からnullまでのパス上に存在する黒ノードの数はすべて同じとし、nullは黒ノードとみなす。
根からnullまでのパス上で赤ノードが連続してはならない。
最後の2つの条件から「根からnullまでパスで最長のものの長さは、最短のものの長さの2倍を超えない」という性質をもちます。つまり平衡二分探索木としての特徴をもつことができるのです。
赤黒木は、探索、挿入、削除などの操作における最悪時間計算量がO(log n)(nは木の要素数)です。実装は面倒ではありますが、実用的なデータ構造として知られています。

木の回転
前提として木の回転を説明しておきます。木の回転とは二分探索木の操作のひとつで、大きい部分木を持ち上げて小さい部分木を下げることで全体の木の高さを低くするために行う処理のことです。回転処理をしても二分探索木の性質は維持されます。以下のアニメーション(Wikipediaより)は視覚的にもわかりやすいです。
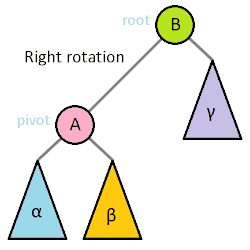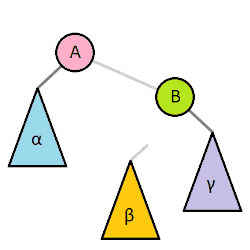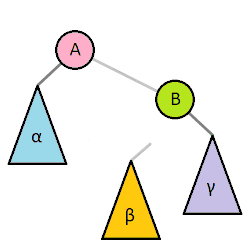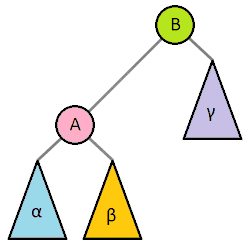
データの追加
データの追加の最初の部分は二分探索木と同じです。根ノードから辿っていき、なにもない部分があったらそこにノードを作成して追加します。そのあと赤黒木としての条件を満たすように調整する必要があります。
ノードは赤として追加します。もしそのノードが一番はじめに追加したノードであれば根となります。根は黒なのでノードの色を黒に変更します。
ノードを追加したときの親が黒ノードであればこれ以上なにもすることはありません。
「赤ノードが連続してはならない」という条件(違反した場合は赤違反とする)には反していないし、「根からnullまでのパス上に存在する黒ノードの数はすべて同じ」という条件(違反した場合は黒違反とする)も満たしたままです。
問題は親が赤ノードだった場合です。このままでは赤違反なので、黒違反にならないように注意しながら調整しなければなりません。
以下、追加されたノードをN、その親をP、親の親をG、親の兄弟をUと表記します。
Uが黒(nullの場合も含む。以下、省略)のとき
外側の子として追加されたとき
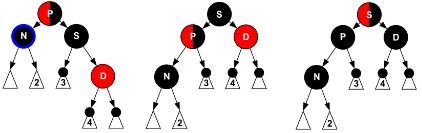
Nが位置するのが外側(PがGの左の子であってNがPの左の子、またはPがGの右の子であってNがPの右の子)である場合はGで回転させます。そしてGがあった位置に来たノードPを黒に、Uがあった位置に来たノードGを赤に変更します。すると図(左:処理前、中央:回転させただけ、右:回転後にノードの色も変更)のようになります。これで赤違反は解消し、黒違反も発生していません。
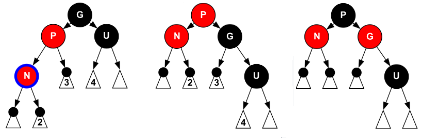
内側の子として追加されたとき
Nが位置するのが内側(PがGの左の子であってNがPの右の子、またはPがGの右の子であってNがPの左の子)である場合はどうでしょうか? この場合は単にGで回転させるだけではうまくいかないので、Pで逆方向に回転させます。すると図(左:処理前、中央:回転後、右:次の回転にそなえてNとPのラベルを貼り直した)のようになります。これは上と同じ形になっているので上と同じ処理をおこないます。
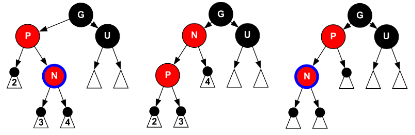
Uが赤のとき
Uが赤のときはPとUの色を黒にしてGを赤にします。これだけだとGの親が赤ノードだと赤違反が解消されたことにはなりません。そこでGをNに代入して処理を繰り返します。すると上記の3パターンのどれかになっているので根まで遡るか、前2者のどちらか、Nの親が黒になっている場合のいずれかになるまでこれを繰り返します。
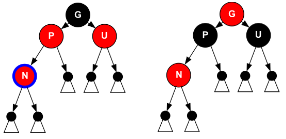
削除の場合
データの削除の最初の部分は二分探索木と同じです。削除するノードの子が存在しない場合はそのまま削除し、子が片方だけ存在する場合は親からその子にむけて参照をセットしなおします。両方の子がいる場合は左の子で最大の値をもつノードを探して、これと値を入れ替え(値だけ入れ替える。色は入れ替えない)、入れ替え先のノードを削除します。
削除したノードが赤ノードである場合、これで処理は終了です。問題は黒ノードを削除した場合です。黒違反や赤違反が起きないように調整が必要です。
それでも削除したノードの子が赤ノードである場合はこれを黒ノードに変更するだけで赤黒双方の違反を解消することができます。それ以外のケースを考えます。
ここでは削除したノードの子は黒ノードかnullであることが前提になります。以下、このノードをNとし、この親をP、Nの兄弟をS、Sの子のうちNに近いほう(NがPの左の子ならSの左の子、NがPの右の子ならSの右の子)をC、遠いほうをDと表記します。
Sが黒である場合
Sが黒である場合、P,C,Dの色で処理をわけます。
PとCとDがすべて黒のとき
Pが赤でCとDが黒のとき
Pが黒または赤、Cが赤、Dが黒のとき
PとCが黒または赤、Dが赤のとき
Pが赤でCとDが黒のとき
順番が前後しますが、簡単なものから。
Pが赤でCとDが黒のときは簡単です。Pの色を黒に、Sの色を赤に変更することで黒違反を解消することができます。図(左:処理前、右:処理後)をみると、処理前はN側の黒の個数が1少ないが処理後は黒違反が解消されていることがわかります。
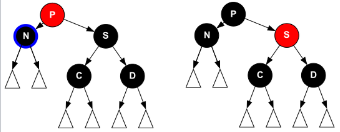
PとCが黒または赤、Dが赤のとき
この場合はPで回転させて回転後にPがあった位置に来たノードSをPの元の色に、その左右の子の位置に来たノードP,Dを黒に変更します。気持ち的にN側では黒が不足しているので回転させてノードを送り込み、ノードを送り込んだ側で発生する黒ノードの不足は赤ノードを黒に変更することで補うという感じです(左:処理前、中央:回転させただけ、右:回転後にノードの色も変更)。
Pが黒または赤、Cが赤、Dが黒のとき
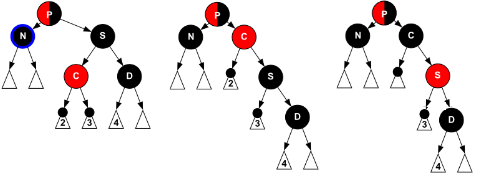
この場合は普通に回転させてもうまくいきません。Dが赤のときは赤ノードで回転にともなう黒ノードの不足を解消することができましたが、今回ははじめから黒ノードなのでノードの色変更で対処することができません。このような場合はSを逆回転させ、Sがあった位置にきたノードCを黒に、Dがあった位置に来たSを赤に変更します(左:処理前、中央:回転させただけ、右:回転後にノードの色も変更)。これで上と同じ形になったのでPで回転処理をおこないます。
PとCとDがすべて黒のとき
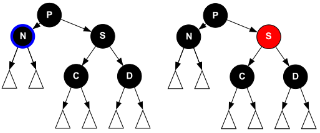
この場合はSを赤に変更します(左:処理前、右:処理後)。するとNと反対側も黒ノードが不足した状態になり、部分木P全体の黒ノードの数が同じになります。しかし、これでは黒違反が解消していないので、NにPを代入して処理を繰り返します。
Sが赤である場合
Sは赤だから、その親と子であるPとCとDは黒でなければなりません。回転処理をしてSとPの色を反転させると以下の図のようになります(左:処理前、中央:回転させただけ、右:回転後にノードの色も変更。△の上の黒丸はこれは△よりも黒深さが1大きいことを示している)。
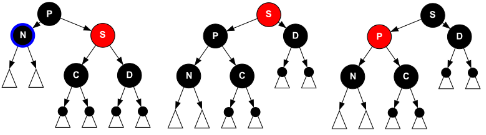
回転後の黒深さを見てみると、CとDの黒深さは同じですが、Nの黒深さはそれよりも1少ない状態は解消されていません。しかし回転処理によってNの兄弟ノードの色は黒に変わるので、もう一度これまでに見た処理のどれかを繰り返すことで赤黒木の性質を取り戻すことができます。
赤黒木の実装
では実装してみることにします。
Nodeクラスの定義
Nodeクラスを以下のように定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
class Node { public Node(long v) { Value = v; } public bool IsBlack = false; public Node Parent = null; public Node[] Children = new Node[2]; public Node Left => Children[0]; public Node Right => Children[1]; public long Value = 0; } |
探索の処理
値が格納されたノードが赤黒木のなかにあるか探索する処理を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
public class RedBlackTree { public bool Search(long v) { if (Root == null) return false; Node cur = Root; while (cur != null) { if (cur.Value == v) return true; cur = cur.Children[v < cur.Value ? 0 : 1]; } return false; } } |
木を回転させる処理
部分木を回転させる処理を示します。第二引数が0のときが左回転、1のときが右回転です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
public class RedBlackTree { // ノードは親からみて左右のどちらにあるか?(0: 左、1: 右) int GetNodeDir(Node node) => (node.Parent == null || node.Parent.Left == node) ? 0 : 1; Node Rotate(Node p, int dir) { Node g = p.Parent; int dir2 = GetNodeDir(p); Node s = p.Children[1 - dir]; Node c = s.Children[dir]; p.Children[1 - dir] = c; if (c != null) c.Parent = p; s.Children[dir] = p; p.Parent = s; s.Parent = g; if (g != null) g.Children[dir2] = s; else Root = s; return s; // 部分木の新しい根 } } |
ノードを追加する処理
ノードを追加する処理を示します。
まず追加する場所を探します。見つかったらその位置にノードを追加します。そのあと赤黒木の条件を満たすように調整を加えます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
public class RedBlackTree { Node Root = null; public int Count = 0; // 格納されているノードの個数 public void Add(long v) { Node parent = Root; bool isLeft = true; while (parent != null) { isLeft = v < parent.Value; Node next = parent.Children[v < parent.Value ? 0 : 1]; if (next != null) parent = next; else break; } Node newNode = new Node(v); if (parent == null) Root = newNode; // 最初は根として追加 else { parent.Children[isLeft ? 0 : 1] = newNode; newNode.Parent = parent; } RebalancingAfterAdd(newNode); // 追加後の処理 Count++; } } |
ノードを追加したあとにおこなう調整の処理です。やっていることは上記のとおりです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
public class RedBlackTree { // Nullも黒ノードとみなすのでtrueを返す bool IsBlack(Node node) => node == null || node.IsBlack; void RebalancingAfterAdd(Node n) { Node p = n.Parent; while (!IsBlack(p)) { Node g = p.Parent; int dir = GetNodeDir(p); Node u = g.Children[1 - dir]; if (IsBlack(u)) { // NはGの内側の孫のときは二重回転が必要 if (n == p.Children[1 - dir]) { Rotate(p, dir); n = p; p = g.Children[dir]; } // 回転させる Rotate(g, 1 - dir); p.IsBlack = true; g.IsBlack = false; break; } else { g.IsBlack = false; u.IsBlack = true; p.IsBlack = true; } n = g; // 新しいカレントノード p = n.Parent; // 新しいNの親が存在しない、または黒なら終了 } // 根は常に黒でなければならない Root.IsBlack = true; } } |
ノードを削除する処理
ノードを削除する処理を示します。
削除の処理がおこなわれたかどうかをチェックするためにbool型の戻り値を返しています。削除すべきノードが見つからないときはfalseを返します。
ここでは普通の二分探索木における削除の処理のみをおこない、赤黒木の条件を満たすための調整の処理はRebalancingAfterRemoveメソッド内でおこなっています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
public class RedBlackTree { public bool Remove(long v) { if (Root == null) return false; Node cur = Root; Node target = null; while (cur != null) { if (cur.Value == v) { target = cur; break; } cur = cur.Children[v < cur.Value ? 0 : 1]; } if (target == null) return false; Node parent = target.Parent; Node removed = null; int dir = GetNodeDir(target); // 削除された子は親からみてどちら側だったかも取得しておく // ノードを親ノードの子として移動させたら子ノードの親も一緒に変更する void SetChild(Node parent, Node child, int dir) { if (parent != null) parent.Children[dir] = child; else Root = child; if (child != null) child.Parent = parent; } if (target.Right == null) { SetChild(parent, target.Left, dir); removed = target; } else if (target.Left == null && target.Right != null) { SetChild(parent, target.Right, dir); removed = target; } else if (target.Left != null && target.Right != null) { Node swapTarget = target.Left; while (swapTarget.Right != null) swapTarget = swapTarget.Right; Swap(target, swapTarget); dir = GetNodeDir(swapTarget); SetChild(swapTarget.Parent, swapTarget.Left, dir); removed = swapTarget; } RebalancingAfterRemove(removed, dir); Count--; return true; } void Swap(Node node1, Node node2) { long v1 = node1.Value; long v2 = node2.Value; node1.Value = v2; node2.Value = v1; } } |
ノードを削除したあと赤黒木の調整をする処理を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
public class RedBlackTree { void RebalancingAfterRemove(Node removed, int dir) { if (Root == null || !IsBlack(removed)) return; Node removedChild = removed.Left != null ? removed.Left : null; if (removedChild == null && removed.Right != null) removedChild = removed.Right; if (!IsBlack(removedChild)) { removedChild.IsBlack = true; return; } Node n = removedChild; Node p = removed.Parent; if (p == null) // n == Root { n.IsBlack = true; return; } Node s = p.Children[1 - dir]; while (s != null) { Node c = s.Children[dir]; Node d = s.Children[1 - dir]; if (IsBlack(s)) { if (IsBlack(c) && IsBlack(d)) { if (!IsBlack(p)) { p.IsBlack = true; s.IsBlack = false; break; } else { s.IsBlack = false; // この場合は上の階層で引き続き調整が必要 n = p; } } else { if (IsBlack(d)) { // この場合は二重回転が必要 Rotate(s, 1 - dir); if (c != null) c.IsBlack = true; s.IsBlack = false; Node temp = s; s = c; c = temp; } Rotate(p, dir); s.IsBlack = p.IsBlack; p.IsBlack = true; if (d != null) d.IsBlack = true; break; } } else { Rotate(p, dir); s.IsBlack = !s.IsBlack; p.IsBlack = !p.IsBlack; } if (n == null) break; dir = GetNodeDir(n); p = n.Parent; if (p == null) break; s = p.Children[1 - dir]; } // 根が存在するときは常に黒 if (Root != null) Root.IsBlack = true; } } |
最大値(最小値)の取得
最大値と最小値を取得する処理を示します。
Rootから左または右へ行けるだけ行った場所にあるノードが探すべきノードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
public class RedBlackTree { public long Max() { long max = long.MinValue; Node cur = Root; while (cur != null) { max = cur.Value; cur = cur.Right; } return max; } public long Min() { long min = long.MaxValue; Node cur = Root; while (cur != null) { min = cur.Value; cur = cur.Left; } return min; } } |
直近の大きな値と小さな値
ある値に近い値を近い順に取得するメソッドを定義しておきます。第二引数で第一引数と同じ値も取得対象とするかどうか、第三引数で最大何個取得するか(-1なら全部)も選べるようにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
public class RedBlackTree { public List<long> GetUnderValues(long v, bool isEqual = true, int maxCount = -1) { List<long> rets = new List<long>(); Dfs(Root); return rets; bool IsEnd() => maxCount != -1 && rets.Count >= maxCount; void Dfs(Node node) { if (node == null) return; bool b = isEqual ? node.Value <= v : node.Value < v; if (node.Right != null && b && !IsEnd()) Dfs(node.Right); if (b && !IsEnd()) rets.Add(node.Value); if (node.Left != null && !IsEnd()) Dfs(node.Left); } } public List<long> GetOverValues(long v, bool isEqual = true, int maxCount = -1) { List<long> rets = new List<long>(); Dfs(Root); return rets; bool IsEnd() => maxCount != -1 && rets.Count >= maxCount; void Dfs(Node node) { if (node == null) return; bool b = isEqual ? node.Value >= v : node.Value > v; if (node.Left != null && b && !IsEnd()) Dfs(node.Left); if (b && !IsEnd()) rets.Add(node.Value); if (node.Right != null && !IsEnd()) Dfs(node.Right); } } } |
