最大長方形問題とは?
最大長方形問題とは「縦に n 行、横に n 列並べられた n × n のタイルがある。いくつかのタイルには印がついている。印のついていないタイルだけで構成される長方形の面積の最大値は?」という問題です。

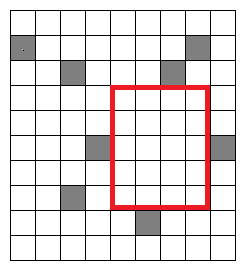
どうやって答えを出せばよいでしょうか? 全体が狭ければ全探索をして一番大きな長方形の面積を求めることができるのかもしれませんが、全体が広い場合は時間がかかってしまいます。
ヒストグラム中の最大の長方形の面積は?
そこで先にヒストグラム中の最大の長方形の面積を考えます。
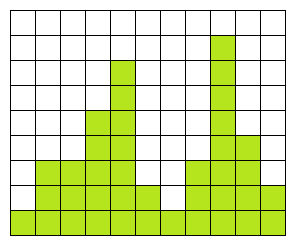
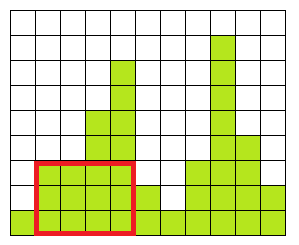
まずは簡単な方法から。2重ループによって配列のなかから底辺になる部分を選び、そのなかから値が最小のものを探します。これが選択された部分で構成することができる長方形の高さになります。あとは得られた値のなかから最大のものを取得します。これはO(n^2)のアルゴリズムです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
using System; using System.Collections.Generic; using System.Linq; internal class Program { static void Main() { int[] values = { 1, 3, 3, 5, 7, 2, 1, 3, 8, 4, 2 }; int max = 0; for (int left = 0; left < values.Length; left++) { for (int right = left; right < values.Length; right++) { // 配列のleft番目からright番目までを底辺とする // このとき配列の最小のものが作ることが出来る長方形の高さにする List<int> ints = new List<int>(); for (int i = left; i <= right; i++) ints.Add(values[i]); int height = ints.Min(); int area = (right - left + 1) * height; max = Math.Max(area, max); } } Console.WriteLine(max); } } |
ただ、もっと速く計算する方法があります。O(n^2)ではなくO(n)にするアルゴリズムが存在するのです。これがスタックを用いた方法です。
まずクラスを定義します。コンストラクタの引数は長方形の高さとその左端の位置です。
|
1 2 3 4 5 6 7 8 9 10 |
public class Rect { public Rect(int left, int height) { Left = left; Height = height; } public int Left = 0; public int Height = 0; } |
ヒストグラムの各長方形の左側の位置と高さでオブジェクトを生成してスタックに入れていくわけですが、そのときに以下の処理をおこないます。
スタックが空の場合はスタックにrectをPushします。またスタックの頂点にある長方形の高さがrectの高さより低い場合もスタックにrectをPushします。そしてスタックの頂点にある長方形の高さが rect の高さと等しい場合は何もしません。
重要なのはスタックの頂点にある長方形の高さがrectの高さより高い場合の処理です。
この場合はスタックが空でなく、スタックの頂点にある長方形の高さが rect の高さ以上である限り、スタックから長方形をPopし、その面積を計算して最大値を更新します。長方形の高さはPopされたオブジェクトのHeightです。また横の長さは現在の位置 i とPopされたオブジェクトのLeftから計算できます。
そのあとスタックにrectをPushします。このときLeftは最後にスタックから取り出した長方形のLeftの値とします。
この場合、例の場合は最初にPushが4回おこなわれます。そのあとスタックの頂点にある長方形の高さより低い高さ(高さ1)のrectが生成されるので、この場合はPopが3回おこなわれ、3つの長方形の面積が計算されます。そして新しく追加されるrectのLeftはPopされた高さ3のrectのLeftと同じ値になります。これを繰り返すことでヒストグラム中の最大の長方形の面積を求めることができます。計算量はO(n)となり、そのぶん速く計算することができるようになりました。
どのような処理がおこなわれているかがわかるように動画にしてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
using System; using System.Collections.Generic; class Program { public class Rect { public Rect(int left, int height) { Left = left; Height = height; } public int Left = 0; public int Height = 0; } static void Main() { int[] values = { 1, 3, 3, 5, 7, 2, 1, 3, 8, 4, 2 }; int max = 0; Stack<Rect> stack = new Stack<Rect>(); // 最後が0で終わるようにしておけばループを抜けたあとの処理が必要なくなる List<int> values2 = new List<int>(values); values2.Add(0); for (int i = 0; i < values2.Count; i++) { if (stack.Count == 0) stack.Push(new Rect(i, values2[i])); else { int height = stack.Peek().Height; if (height < values2[i]) stack.Push(new Rect(i, values2[i])); else if (height > values2[i]) { Rect lastPop = null; while (stack.Count > 0 && values2[i] <= stack.Peek().Height) { Rect rect = stack.Pop(); int area = (i - rect.Left) * rect.Height; lastPop = rect; max = Math.Max(area, max); } if (lastPop != null) stack.Push(new Rect(lastPop.Left, values2[i])); } } } Console.WriteLine(max); } } |
最大長方形問題を解く
ヒストグラム中の最大長方形問題を解くときのアルゴリズムを用いて最大長方形問題を解くことができます。まず各要素について上に向かってtrueが何個連続しているかを示す配列のリストを作ります。次にリストに格納されている配列をヒストグラムの入力と見なしヒストグラムの最大長方形の面積を求める処理をおこないます。

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
using System; using System.Collections.Generic; class Program { public class Rect { public Rect(int left, int height) { Left = left; Height = height; } public int Left = 0; public int Height = 0; } static void Main() { string[] map = { ".........", "#......#.", "..#...#..", ".........", ".........", "...#....#", ".........", "..#......", ".....#...", }; List<int[]> valuesList = new List<int[]>(); int rowCount = map.Length; int colCount = map[0].Length; for (int row = 0; row < rowCount; row++) valuesList.Add(new int[colCount + 1]); for (int row = 0; row < rowCount; row++) { for (int col = 0; col < colCount; col++) { if (row == 0) valuesList[0][col] = map[0][col] == '.' ? 1 : 0; else valuesList[row][col] = map[row][col] == '.' ? valuesList[row - 1][col] + 1 : 0; } } int max = 0; foreach (int[] values in valuesList) { Stack<Rect> stack = new Stack<Rect>(); for (int i = 0; i < values.Length; i++) { if (stack.Count == 0) stack.Push(new Rect(i, values[i])); else { int height = stack.Peek().Height; if (height < values[i]) stack.Push(new Rect(i, values[i])); else if (height > values[i]) { Rect lastPop = null; while (stack.Count > 0 && values[i] <= stack.Peek().Height) { Rect rect = stack.Pop(); int area = (i - rect.Left) * rect.Height; lastPop = rect; max = Math.Max(area, max); } if (lastPop != null) stack.Push(new Rect(lastPop.Left, values[i])); } } } } Console.WriteLine(max); } } |
