当ブログはネタ切れをおこすと数学ネタに走る傾向があります。YouTubeで公開されているある動画をみてC#でマンデルブロ集合を描くことに挑戦してみました。
元ネタはこちらです。ヘロンの数学さんの動画です。
Contents
マンデルブロ集合をC#で描画する
ところでマンデルブロ集合とは何でしょうか? マンデルブロ集合は以下で定義される複素数列が n → ∞ の極限で無限大に発散しないという条件を満たす複素数が作る集合です。
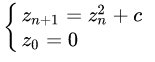
C#では複素数を扱うためのクラスが用意されています。それがSystem.Numerics名前空間のComplexクラスです。これを使うためには参照にSystem.Runtime.Numerics.dllを追加しなければなりません。
複素数cに対してz = z * z + cを繰り返し計算して一度でもzの絶対値が2を超えてしまうとこの複素数列zは発散してしまうことが証明されています。そこでこんな関数を使えば複素数cに対して複素数列zが発散するかどうか、cがマンデルブロ集合に属するかどうかを調べることができます。まずは30回、z = z * z + cを計算して絶対値zが2を超えなければマンデルブロ集合であると判断します。
このメソッドは引数cがマンデルブロ集合に属する場合、trueを返します。
マンデルブロ集合に属するか判定するメソッド
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
public partial class Form1 : Form { bool IsMandelbrotSet(Complex c) { int count = 30; Complex z = Complex.Zero; for (int i = 0; i < count; i++) { z = z * z + c; if (z.Magnitude > 2) return false; } return true; } } |
まずは幅800ピクセル、高さ400ピクセルのBitmapをつくります。1ピクセルを0.005として、実部-2から+2、虚部-1から+1まで総当たりで調べます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
public partial class Form1 : Form { Bitmap Bitmap = new Bitmap(800, 400); double ParDot = 0.005; public Form1() { InitializeComponent(); CreateMandelbrotSetBitmap(); ClientSize = new Size(Bitmap.Width, Bitmap.Height); } void CreateMandelbrotSetBitmap() { Graphics graphics = Graphics.FromImage(Bitmap); graphics.Clear(Color.White); graphics.Dispose(); for (int x = 0; x < Bitmap.Width; x++) { for (int y = 0; y < Bitmap.Height; y++) { Complex c = new Complex( -2 + x * ParDot, -1 + y * ParDot ); if (IsMandelbrotSet(c)) { Bitmap.SetPixel(x, y, Color.Black); } } } } protected override void OnPaint(PaintEventArgs e) { // 数学の座標と異なりY軸は下が正になっているので上下反転させる Bitmap clone = (Bitmap)Bitmap.Clone(); clone.RotateFlip(RotateFlipType.RotateNoneFlipY); e.Graphics.DrawImage(clone, new Point(0, 0)); clone.Dispose(); base.OnPaint(e); } bool IsMandelbrotSet(Complex c) { int count = 30; Complex z = Complex.Zero; for (int i = 0; i < count; i++) { z = z * z + c; if (z.Magnitude > 2) return false; } return true; } } |
するとこのようなこのように描画されます。一応、それっぽいものが描画されています。

マンデルブロ集合を拡大して描画する
一部を拡大して描画する方法を考えることにします。
マンデルブロ集合はフラクタル図形として表され、周囲を拡大すると、このフラクタル図形に類似した飛び地のような図形が無数に見られることが知られています。しかし実際にはマンデルブロ集合全体は「飛び地」のようにみえても実際には連結であることが証明されています。
まずクリックされた場所を中心にして2倍に拡大して表示させることにします。Bitmapの幅と高さが決まっていて中心になる複素数の実部と虚部が決まるのであれば、左上になる複素数の実部と虚部も決まります。
最初はBitmapの幅、高さを800ピクセルと400ピクセルにしましたが、マンデルブロ集合は実部は-2から+1未満、虚部も-1から+1以内に収まります。だからBitmapは幅650ピクセル、高さ450ピクセルに変更します。また中心に表示させるのは実部-0.5、虚部0の部分にします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
public partial class Form1 : Form { Bitmap Bitmap = new Bitmap(800, 400); double ParDot = 0.005; double CenterX = -0.5; double CenterY = 0; public Form1() { InitializeComponent(); CreateMandelbrotSetBitmap(); ClientSize = new Size(Bitmap.Width, Bitmap.Height); } } |
Bitmapの(0,0)の座標にくるのは評価対象となる複素数の実部と虚部の最小値です。中心にくる評価対象となる複素数の値とBitmapのサイズ、1ドットの値から複素数の実部と虚部の最小値は以下のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
public partial class Form1 : Form { double RealMin { get { return CenterX - ParDot * Bitmap.Width / 2; } } double ImaginarylMin { get { return CenterY - ParDot * Bitmap.Height / 2; } } } |
これをつかってBitmapの中に描画される複素数の範囲内だけマンデルブロ集合に属するかどうかを判定するメソッドを書くとすると以下のようになります。
CreateMandelbrotSetBitmapメソッドを改良する
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
public partial class Form1 : Form { void CreateMandelbrotSetBitmap() { Graphics graphics = Graphics.FromImage(Bitmap); graphics.Clear(Color.White); graphics.Dispose(); for (int x = 0; x < Bitmap.Width; x++) { for (int y = 0; y < Bitmap.Height; y++) { Complex c = new Complex( RealMin + x * ParDot, ImaginarylMin + y * ParDot ); if (IsMandelbrotSet(c)) { Bitmap.SetPixel(x, y, Color.Black); } } } } } |
クリックされたら拡大する処理
マウスが動いたらマウスがある座標はどのような複素数の値に相当する部分なのかがわかるようにタイトルバーに表示させます。
|
1 2 3 4 5 6 7 8 9 10 11 |
public partial class Form1 : Form { protected override void OnMouseMove(MouseEventArgs e) { double x = RealMin - e.X * ParDot; double y = ImaginarylMin + (Bitmap.Height - e.Y) * ParDot; Text = $"X = {x}, Y = {y} ParDot = {ParDot}"; base.OnMouseMove(e); } } |
そしてクリックされたらその点を中心に拡大/縮小します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
public partial class Form1 : Form { protected override void OnMouseDown(MouseEventArgs e) { CenterX = e.X * ParDot + RealMin; CenterY = (Bitmap.Height - e.Y) * ParDot + ImaginarylMin; if(e.Button == MouseButtons.Left) ParDot *= 0.5; if (e.Button == MouseButtons.Right) ParDot /= 0.5; CreateMandelbrotSetBitmap(); Invalidate(); base.OnMouseDown(e); } } |
拡大するとマンデルブロ集合らしくなるのはなぜ?
これで完成といいたいところなのですが、実際に拡大処理を繰り返してみると繰り返すごとにマンデルブロ集合らしくなくなっていくのです。
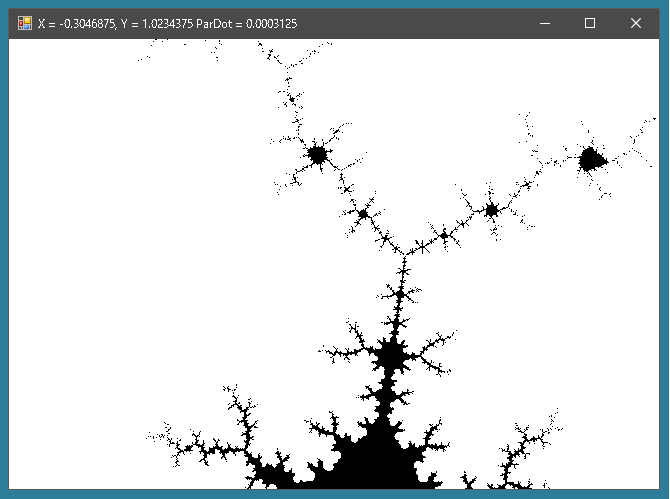
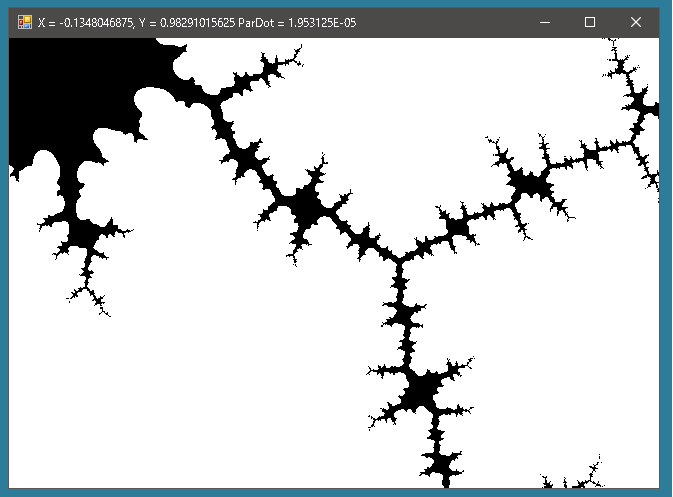

これは数字の違いがだんだん小さくなっていくからで、最初のほうは30回処理を繰り返して絶対値が2を超えない場合はマンデルブロ集合に属すると判断してもかまわないが、拡大していくにしたがってもっと多くの計算が求められることを意味しています。
IsMandelbrotSetメソッドのなかでは30回処理を繰り返して絶対値が2を超えない場合はマンデルブロ集合に属すると判断していますが、処理時間が長くなるけれども30回ではなくもっと増やせばより正確な形になるのではないかと思われます。
では30回ではなく300回にしてみましょう。すると今度は別の問題がおきます。マンデルブロ集合は連続しているのですが、バラバラの点が目立つようになるのです。これは近くにマンデルブロ集合に属する複素数が存在するが、評価対象の複素数はマンデルブロ集合に属さないからです。
そのため点がバラバラに存在するように見えてしまいます。
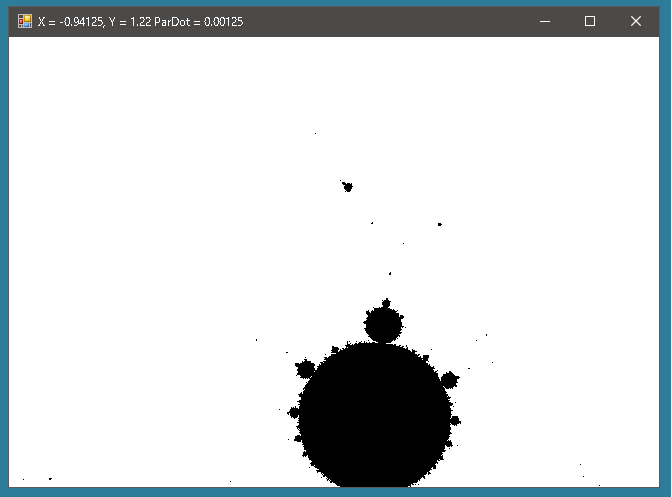
しかし拡大率をあげると連続していることがわかります。
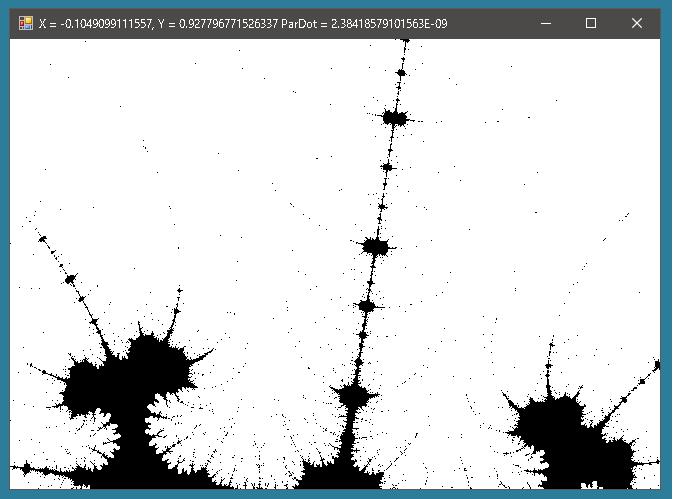
そこで最初は反復回数は30回くらいで開始して、拡大率が大きくなったときは反復回数を増やすようにします。当然のことながら反復回数を増やせば処理にかかる時間は長くなります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
public partial class Form1 : Form { int NumberOfTrials = 30; bool IsMandelbrotSet(Complex c) { Complex z = Complex.Zero; for (int i = 0; i < NumberOfTrials; i++) { z = z * z + c; if (z.Magnitude > 2) return false; } return true; } protected override void OnMouseDown(MouseEventArgs e) { CenterX = e.X * ParDot + RealMin; CenterY = (Bitmap.Height - e.Y) * ParDot + ImaginarylMin; if (Control.ModifierKeys != Keys.Control) { if (e.Button == MouseButtons.Left) ParDot *= 0.5; if (e.Button == MouseButtons.Right) ParDot /= 0.5; } if (Control.ModifierKeys == Keys.Control) { if (e.Button == MouseButtons.Left) NumberOfTrials += 10; if (e.Button == MouseButtons.Right && NumberOfTrials > 30) NumberOfTrials -= 10; } CreateMandelbrotSetBitmap(); Invalidate(); base.OnMouseDown(e); } } |
これだとそれっぽいものが描画されます。試行回数を30回から60回に増やすだけでこんなにもかわります。
試行回数30回
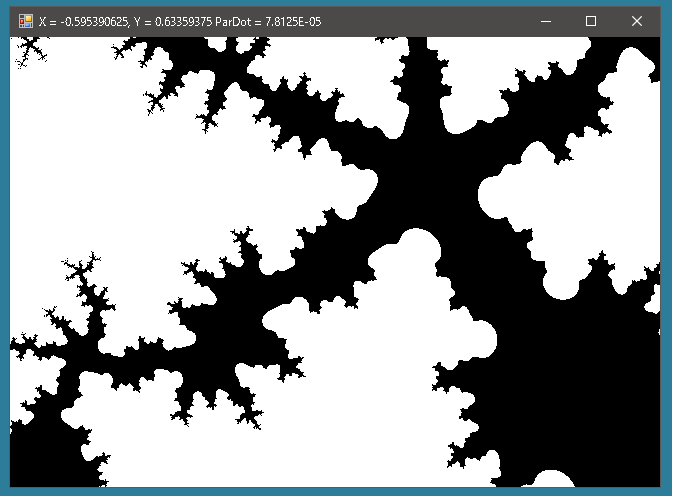
試行回数60回
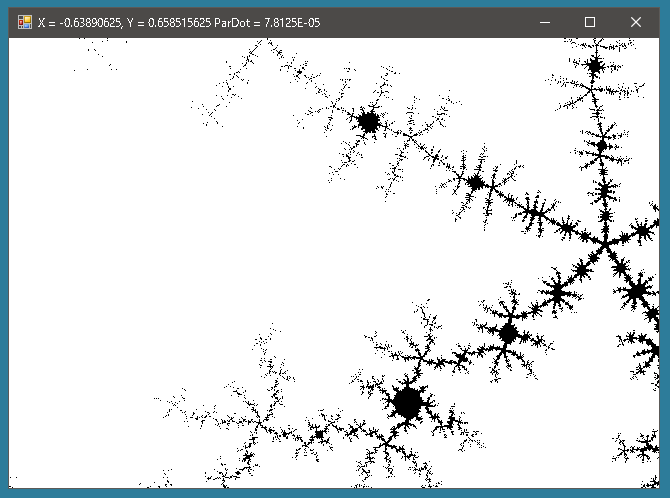
ただdouble型の範囲を超えてしまうとどうすることもできません。
