AVL木(AVL tree、Adelson-Velskii and Landis’ tree)は二分探索木の一種(そのなかでも平衡二分探索木の一種)です。
Contents
二分探索木とは?
二分探索木とはこの図のようなものです。
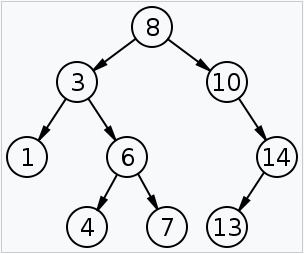
各ノードは最大2つの子ノードを持ち、左の子ノードは親よりも小さく、右の子ノードには親以上の値が格納されます。左右のバランスがとれている状態では高速にデータを検索することができます。もっとも理想的な状態だと時間計算量は O(logN) となります。格納されているデータの数が1000の場合、10回程度の比較で目的のデータを見つけることができるのです。
探索
木の中から目的の値を持つノードを見つけ出すのが探索です。二分探索木は親よりも左の子は値が小さく、右の子は親以上の値が格納されているという性質があるので、以下の方法で探索することができます。
まず、根ノードに着目します。着目しているノードが存在しなければ、木に目的の値を持つノードはないので処理を終了します。
もし着目しているノードが存在するときは、その値と目的の値を比較します。値が等しいのであれば探索は終了です。探している値が着目しているノードの値よりも小さいのであれば、着目するノードを左の子ノードに切り替えます。逆に探している値が着目しているノードの値以上であるのであれば着目するノードを右の子ノードに切り替えます。
このような処理を繰り返すことで目的の値をもつノードを見つけ出すことができます。
追加
値を追加するときも探索と同じようにして根ノードから辿っていき、なにもない部分があったらそこにノードを作成して追加します。追加したい値と同じ値をもつノードが出現した場合はその右の子として追加します。
削除
削除するときは探索と同じ手順で削除対象となるノードを探します。見つかったら以下のケースで場合分けをして処理をおこないます。
① 削除ノードが子どもを持たない場合
そのノードをそのまま削除する。
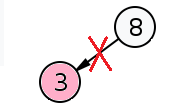
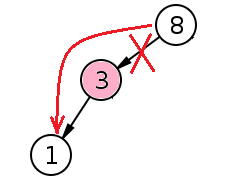
② 左右の子のうち片方しかもたない場合
削除ノードを削除してその子と置き換える。
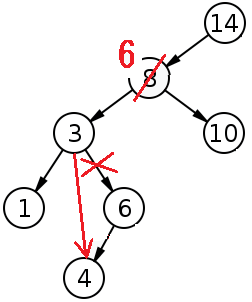
③ 両方の子を持つ場合
削除したいノードの左の子の子孫から最大の値を探す。
見つかったノードと削除対象のノードの値を入れ替え、入れ替え先のノードを削除する。
入れ替え先のノードが左の子をもつときはこれを入れ替え先の親ノードの子とする。
単純な二分探索木の欠陥と平衡二分探索木
単純な二分探索木の欠点として、値が格納される順序によっては左右のバランスが悪くなってしまうことが挙げられます。これでは二分探索木の利点を活かすことができなくなります。
そこで考案されたのが平衡二分探索木です。うまく工夫することでバランスが取れた木を構築することができ、データの検索、追加、削除を高速におこなえるようになります。
AVL木の特徴
AVL木も平衡二分探索木のひとつです。データの追加、削除に伴って左右のバランスが崩れたときに「回転」と呼ばれる操作を行うことで平衡を維持することができます。
AVL木はどのノードであっても左右部分木の高さの差は1以下であるという特徴があります。この性質によって探索の計算量を常に O(logN)程度にすることを保証しています。
平衡係数
AVL木は各ノードの左右に子ノードを持ちますが、この子ノードを根とする部分木の高さの差を平衡係数と定義します。要素が追加されたり削除されたら平衡係数を調べて、その絶対値が 2 以上になったら回転処理をおこなって平衡係数の絶対値が 1 以下になるようにします。
回転
二分探索木の操作の一種で、要素の順序を崩さずに構造を変更するものである。
木の回転は大きい部分木を持ち上げて小さい部分木を下げることで全体の木の高さを低くするために行う処理です。ここでは二分探索木がもつ性質を維持されます。以下のアニメーション(Wikipediaより)は視覚的にもわかりやすいです。
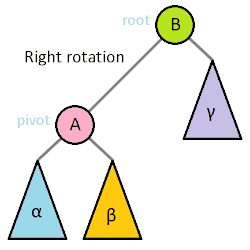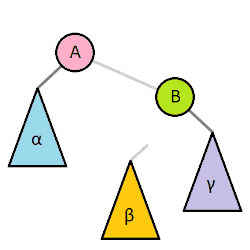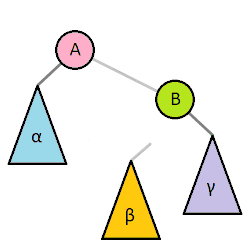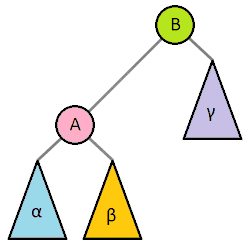
そのうえで注意点があります。
平衡係数の差の絶対値が 2 になってしまった場合、部分木が高いほうから低いほうへ回転させればよいのですが、単純な回転では平衡条件が満たされない場合があります。具体的には以下の場合です。
① 親ノードの左部分木の方が高く、かつその左の子ノードの右部分木の方が高い場合
② 親ノードの右部分木の方が高く、かつその右の子ノードの左部分木の方が高い場合
① の場合は親の左の子ノードで左回転をおこない、そのあと親ノードの右回転処理をおこないます。また ② の場合は親の右の子ノードで右回転をおこない、そのあと左回転処理をおこないます。
追加と削除の処理
ノードの追加と削除は二分探索木における追加と同じようにすればよいのですが、そのあと平衡係数を調べてその絶対値が 2 以上になっている場合は適切に回転処理をしなければなりません。
回転処理が必要かどうかは、まずノードを追加した親でおこない、そのあと根に向かってさかのぼるように進めていきます。
実装
ではAVL木を実装してみましょう。
Nodeクラスの定義
まずNodeクラスを定義します。平衡係数を計算できるようにそのノードの高さ(そのノードから葉=子ノードを持たないノードへの最長距離)を保存できるようにしておきます。
ノードの高さはふたつの子ノードの高さのうち大きいほうに1を加えたものです。子ノードが存在しない場合(初期状態)の高さは 1 です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
public class AvlTree { class Node { public Node(long v) { Value = v; Height = 1; } // 左右の子ノードの高さの差から平衡係数を求める public int GetEquilibriumFactor() { int h0 = Children[0] == null ? 0 : Children[0].Height; int h1 = Children[1] == null ? 0 : Children[1].Height; return h0 - h1; } // ノードの高さを更新する public bool UpdateHeight() { int old = Height; int height = Children[0] == null ? 0 : Children[0].Height; height = Math.Max(height, Children[1] == null ? 0 : Children[1].Height); Height = height + 1; return old != Height; } public long Value = 0; public Node[] Children = new Node[2]; public int Height = 0; } } |
探索処理
探している値と着目しているノードの値を比較して左または右の子ノードをたどっていき、探している値が格納されているノードがあるかどうか調べます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
public class AvlTree { Node Root = null; public bool Search(long v) { if (Root == null) return false; Node cur = Root; while (cur != null) { if (cur.Value == v) return true; cur = cur.Children[v < cur.Value ? 0 : 1]; } return false; } } |
回転処理
左右の回転処理を示します。引数は回転させたい部分木の根であり、戻り値は回転後の部分木の根になるノードです。回転することでノードの高さが変わるので回転で影響をうけるノードの高さを再計算する処理も合わせておこないます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
public class AvlTree { Node RotateR(Node node) { if (node.Children[0] == null) return null; Node b = node.Children[0]; Node c = node.Children[0].Children[1]; node.Children[0] = c; b.Children[1] = node; node.UpdateHeight(); b.UpdateHeight(); return b; } Node RotateL(Node node) { if (node.Children[1] == null) return null; Node b = node.Children[1]; Node c = node.Children[1].Children[0]; node.Children[1] = c; b.Children[0] = node; node.UpdateHeight(); b.UpdateHeight(); return b; } } |
追加の処理
ノードを追加する処理を示します。ノードを追加したら根までさかのぼって平衡係数を調べて必要であれば回転処理をおこなわなければなりません。そのため根から新たにノードを追加する親までにたどった親ノードとその方向をStackに保存しています。ノードを追加したらノードの高さの更新と平衡係数の計算、回転処理をおこないます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
public class AvlTree { public void Add(long v) { Node node = new Node(v); if (Root == null) { Root = node; return; } Node cur = Root; Stack<Node> parents = new Stack<Node>(); Stack<bool> isLefts = new Stack<bool>(); while (cur != null) { parents.Push(cur); isLefts.Push(v < cur.Value); cur = cur.Children[v < cur.Value ? 0 : 1]; } parents.Peek().Children[isLefts.Peek() ? 0 : 1] = node; RotateParents(parents, isLefts); } } |
ノードを追加削除後にノードの高さの更新と平衡係数の計算、回転処理をおこなう部分の処理を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
public class AvlTree { void RotateParents(Stack<Node> parents, Stack<bool> isLefts) { while (parents.Count > 0) { Node parent = parents.Pop(); bool isLeft = isLefts.Pop(); // ノードの高さを更新する必要がない場合は // それより根側でも更新されることはないのでここで終了 if (!parent.UpdateHeight()) return; int ef = parent.GetEquilibriumFactor(); // 平衡係数 if (ef > 1) // 左回転が必要な場合 { if (parent.Children[0].GetEquilibriumFactor() < 0) // 二重回転が必要な場合 parent.Children[0] = RotateL(parent.Children[0]); // 回転させたら部分木の根をその親とつながるようにしておく Node newParent = RotateR(parent); if (parents.Count > 0) parents.Peek().Children[isLefts.Peek() ? 0 : 1] = newParent; else Root = newParent; } else if (ef < -1) // 右回転が必要なときも同様 { if (parent.Children[1].GetEquilibriumFactor() > 0) parent.Children[1] = RotateR(parent.Children[1]); Node newParent = RotateL(parent); if (parents.Count > 0) parents.Peek().Children[isLefts.Peek() ? 0 : 1] = newParent; else Root = newParent; } } } } |
削除の処理
ノードを削除する処理を示します。追加するときと同様、ノードを削除したら根までさかのぼって平衡係数を調べて必要であれば回転処理をおこないます。削除するとき左の子の子孫のなかから最大値をもつノードを調べてこれと入れ替えてから削除する処理が必要な場合がありますが、この場合はさかのぼる処理の開始点は入れ替えた先の親ノードとなります(削除対象ノードがあった位置よりも深いところからなので注意!)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
public class AvlTree { public void Remove(long v) { if (Root == null) return; Node cur = Root; Node target = null; Stack<Node> parents = new Stack<Node>(); Stack<bool> isLefts = new Stack<bool>(); while (cur != null) { if (cur.Value == v) { target = cur; break; } parents.Push(cur); isLefts.Push(v < cur.Value); cur = cur.Children[v < cur.Value ? 0 : 1]; } if (target == null) return; if (target.Children[1] == null) { if (parents.Count > 0) parents.Peek().Children[isLefts.Peek() ? 0 : 1] = target.Children[0]; else Root = target.Children[0]; } else if (target.Children[0] == null && target.Children[1] != null) { if (parents.Count > 0) parents.Peek().Children[isLefts.Peek() ? 0 : 1] = target.Children[1]; else Root = target.Children[1]; } else if (target.Children[0] != null && target.Children[1] != null) { // 削除対象ノードがふたつの子ノードを持っていた場合はちょっと面倒くさい parents.Push(target); isLefts.Push(true); cur = target.Children[0]; while (cur.Children[1] != null) { parents.Push(cur); isLefts.Push(false); cur = cur.Children[1]; } Swap(target, cur); parents.Peek().Children[isLefts.Peek() ? 0 : 1] = cur.Children[0]; } RotateParents(parents, isLefts); } void Swap(Node node1, Node node2) { long v1 = node1.Value; long v2 = node2.Value; node1.Value = v2; node2.Value = v1; } } |
これで基本的な部分は終わりですが、他にも使えそうな機能を追加してみることにします(そうでないと自作する意味がない)。
最大値と最小値
根から左へたどれるだけたどると最小値が、右へたどれるだけたどると最大値を取得できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
public class AvlTree { public long Max() { long max = long.MinValue; Node cur = Root; while (cur != null) { max = cur.Value; cur = cur.Children[1]; } return max; } public long Min() { long min = long.MaxValue; Node cur = Root; while (cur != null) { min = cur.Value; cur = cur.Children[0]; } return min; } } |
直近の大きな値と小さな値
ある値に一番近い値(または K 番目に近い値)を取得しないといけないケースはけっこうあるのでそのようなメソッドも定義しておきます。
第二引数で第一引数と同じ値も取得対象とするかどうか、第三引数で最大何個取得するか(-1なら全部)も選べるようにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
public class AvlTree { public List<long> GetOvers(long v, bool isEqual = true, int maxCount = -1) { List<long> rets = new List<long>(); Dfs(Root); return rets; void Dfs(Node node) { if (node == null) return; bool b1 = isEqual ? node.Value >= v : node.Value > v; bool b2 = maxCount == -1 ? true : rets.Count < maxCount; if (!b2) return; if (node.Children[0] != null && b1) Dfs(node.Children[0]); if (b1 && b2) rets.Add(node.Value); if (node.Children[1] != null) Dfs(node.Children[1]); } } public List<long> GetUnders(long v, bool isEqual = true, int maxCount = -1) { List<long> rets = new List<long>(); Dfs(Root); return rets; void Dfs(Node node) { if (node == null) return; bool b1 = isEqual ? node.Value <= v : node.Value < v; bool b2 = maxCount == -1 ? true : rets.Count < maxCount; if (!b2) return; if (node.Children[1] != null && b1) Dfs(node.Children[1]); if (b1 && b2) rets.Add(node.Value); if (node.Children[0] != null) Dfs(node.Children[0]); } } } |
