ひとりで勝手にはじめた蟻本読書会 最大流問題と最小カット問題 蟻本読書会 の続きです。
二部グラフの最大マッチング問題
グラフ理論における二部グラフとは、頂点集合を2つに分割して各部分の頂点は互いに隣接しないようにできるグラフです。一般に互いに隣接しない頂点からなる集合を独立集合といい、頂点集合を n 個の独立集合に分割可能なグラフのことを n 部グラフといいます。
マッチングとは,端点を共有しない枝の集合です。グラフが与えられたときに要素数最大のマッチングを求める問題を最大マッチング問題といいます。
最大流問題は二部グラフの最大マッチング問題を解くときにも使えます。二部グラフの左にsource、右にsinkを配置し、sourceとAの各頂点、sinkとBの各頂点をリンクで繋ぎ、各リンクの容量を1とすると、最大マッチングは最大流と一致するのです。
C – 2D Plane 2N Points
二次元平面に,赤い点と青い点が N 個ずつあります。i 個目の赤い点の座標は (a_i, b_i) で i 個目の青い点の座標は (c_i, d_i) です。合計 N × 2 個の点はすべて異なる座標にあります。またX座標であったりY座標が同じ点はありません。
赤い点と青い点は、赤い点の x 座標が青い点の x 座標より小さく、赤い点の y 座標も青い点の y 座標より小さいときに仲良しペアになれます。
最大で何個の仲良しペアを作ることができますか? ただし 1 つの点が複数のペアに所属することはできません。
入力されるデータ
N
a_1 b_1
a_2 b_2
…
a_N b_N
c_1 d_1
c_2 d_2
…
c_N d_N
(ただし 1 ≦ N ≦ 100, 0 ≦ a_i, b_i, c_i, d_i < 2N)
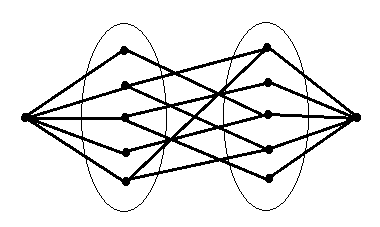
source と sink、そして赤い点を表す頂点、青い点を表す頂点をつくります。赤と青の点はそれぞれ N 個ずつあるので頂点は全部で 2 * N + 2 個になります。そしてsource と赤い点を表す頂点を辺でつなぎます。さらに仲良しペアになれる赤い点を表す頂点と青い点を表す頂点を容量 1 の辺でつなぎます。最後に青い点を表す頂点と sink を辺でつなぎます。
こうしてできたグラフの最大流問題を考えます。これがこの問題の解となります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 |
using System; using System.Collections.Generic; using System.Linq; class Position { public Position(int num, int x, int y) { Number = num; X = x; Y = y; } public int Number { get; } public int X { get; } public int Y { get; } } class Program { static void Main() { int N = int.Parse(Console.ReadLine()); List<Position> Rs = new List<Position>(); for (int i = 0; i < N; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int a = vs[0]; int b = vs[1]; Rs.Add(new Position(i, a, b)); } List<Position> Bs = new List<Position>(); for (int i = 0; i < N; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int c = vs[0]; int d = vs[1]; Bs.Add(new Position(i, c, d)); } // 隣接リストをつくる // 頂点の番号は // source = 0 // Rs[0] ~ Rs[N - 1] = 1 ~ N // Bs[0] ~ Bs[N - 1] = N + 1 ~ N * 2 // sink = N * 2 + 1 とする int vertexCount = N * 2 + 2; Dictionary<int, int>[] edges = new Dictionary<int, int>[vertexCount]; for (int i = 0; i < vertexCount; i++) edges[i] = new Dictionary<int, int>(); // source と赤い点を表す頂点を辺でつなぐ for (int i = 1; i <= N; i++) { edges[0].Add(i, 1); edges[i].Add(0, 0); // 逆辺 } // 青い点を表す頂点と sink を辺でつなぐ for (int i = N + 1; i <= N * 2; i++) { edges[i].Add(N * 2 + 1, 1); edges[N * 2 + 1].Add(i, 0); // 逆辺 } // 仲良しペアになれる赤い点を表す頂点と青い点を表す頂点を容量 1 の辺でつなぐ for (int i = 0; i < N; i++) { // 赤い点と仲良しペアになれる青い点を探す List<Position> bs = Bs.Where(_ => Rs[i].X < _.X && Rs[i].Y < _.Y).ToList(); foreach (Position pos in bs) { // R[i] と B[i] の頂点番号はそれぞれ i + 1, N + i + 1 なので・・・ edges[i + 1].Add(N + pos.Number + 1, 1); edges[N + pos.Number + 1].Add(i + 1, 0); // 逆辺 } } // フローを流せなくなるまで流す long total = 0; while (true) { long flow = BFS(edges, vertexCount, 0, vertexCount - 1); total += flow; if (flow == 0) break; } Console.WriteLine(total); } static long BFS(Dictionary<int, int>[] edges, int N, int start, int goal) { // 増加道を探す int[] froms = new int[N]; bool[] visits = new bool[N]; Queue<int> q = new Queue<int>(); q.Enqueue(start); visits[start] = true; while (q.Count > 0) { int cur = q.Dequeue(); foreach (var edge in edges[cur]) { int next = edge.Key; if (visits[next] || edge.Value <= 0) continue; visits[next] = true; froms[next] = cur; q.Enqueue(next); } } // 増加道が見つかったらフローを流す if (visits[goal]) { int last = goal; List<int> list = new List<int>(); list.Add(last); while (last != start) { int from = froms[last]; last = from; list.Add(last); } list.Reverse(); int min = int.MaxValue; for (int i = 0; i < list.Count - 1; i++) { int from = list[i]; int next = list[i + 1]; min = Math.Min(min, edges[from][next]); } for (int i = 0; i < list.Count - 1; i++) { int from = list[i]; int next = list[i + 1]; edges[from][next] -= min; edges[next][from] += min; } return min; } else return 0; } } |
