行列を用いて連立一次方程式を解く方法は 掃き出し法で連立一次方程式を解く 逆行列と行列式を求める でやりました。
掃き出し法(ガウス・ジョルダン Gauss-Jordan 法)
連立方程式を 行列 と 列ベクトル で表します。
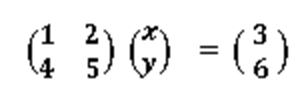
以下のようなものを拡大係数行列と呼びます。

行列 A * 列ベクトル b を変形して左辺の行列を単位行列のしてしまえば連立方程式を解くことができたことになります。これを変形させて以下のような形に変化させれば方程式を解いたことになります。

掃き出し法は、ある行列に対して行の基本変形を繰り返し行い、階段行列に変形する際に利用する一連の操作のことです。ガウス・ジョルダン(Gauss-Jordan)法とも言います。
行の基本変形とは行列の基本変形とは、①行を入れ替える、②ある行を0ではない定数で定数倍すること、③ある行に他の行の定数倍を加えることです。
この行列による式が連立方程式を意味しています。そのうえで「行を入れ替える」ことは式の順番を入れ替えることを意味します。この操作によって連立方程式の解が変わることはありません。「ある行を0ではない定数で定数倍する」ことも連立方程式の解を変えません。「ある行に他の行の定数倍を加える」ことは連立方程式を解くときに用いる加減法と同じ操作です。これももちろん連立方程式の解を変化させることはありません。
ではどのように行を入れ替えたり、ある行を定数倍したり、これを他の行に加える処理をすればよいのでしょうか?
まず i 行 i 列の行列の要素をみていきます。左上から斜めに見ていけばよいです。もし 0 がみつかった場合、それより下にある係数が0でない行を探します。該当する行がみつかっったら行を入れ替えます。もし見つからない場合は連立方程式は不定形または不能形です。
行を入れ替えて i 行 i 列の要素が 0 でなくなったら、これを 1 にするために行全体を割り算します。そのあと i 行以外の行の i 列の要素が 0 になるような定数を求めて定数倍を加えます。こうして行列 A を単位行列に変えていきます。
以下のコードは上記の掃き出し法で連立方程式
4x + 9y + 7z = 74
5x – 4y + 6z = 8
7x – 6y + 10z = 14
の解を計算しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
using System; using System.Collections.Generic; public class Program { static bool GaussJordan(double[,] mat) { int rowCount = mat.GetLength(0); int colCount = mat.GetLength(1); for (int row = 0; row < rowCount; row++) { double value = mat[row, row]; // 係数が0だった場合、それより下にある係数が0でない行を探す // 見つかったら行を入れ替える。見つからない場合は不定形または不能形 if (value == 0) { for (int anotherRow = row + 1; anotherRow < rowCount; anotherRow++) { // 係数が0でない行がみつかったので行を入れ替える if (mat[anotherRow, row] != 0) { for (int col = 0; col < colCount; col++) { double d = mat[anotherRow, col]; mat[anotherRow, col] = mat[row, col]; mat[row, col] = d; } break; } } value = mat[row, row]; if (value == 0) { // 係数が0ではない行は見つからない場合は不定形または不能形。処理を終了する return false; } } for (int col = 0; col < colCount; col++) mat[row, col] /= value; // 他の行に mat[row, row] を 1 にした行の定数倍を加えて他の行のrow列を 0 にする for (int otherRow = 0; otherRow < rowCount; otherRow++) { if (otherRow == row) continue; double ratio = mat[otherRow, row]; for (int col = 0; col < colCount; col++) mat[otherRow, col] -= ratio * mat[row, col]; } } return true; } static void Main() { double[,] mat = { {4, 9, 7, 74,}, {5, -4, 6, 8,}, {7, -6, 10, 14,}, }; if (GaussJordan(mat)) { int rowCount = mat.GetLength(0); int colCount = mat.GetLength(1); List<double> solution = new List<double>(); for (int row = 0; row < rowCount; row++) solution.Add(mat[row, colCount - 1]); Console.WriteLine("解は " + string.Join(", ", solution)); } else Console.WriteLine("不定形または不能形です"); } } |
応用問題
D – 数列 XOR
長さ N の 2 つの整数列 (A_1, A_2, …, A_N), (B_1, B_2, …, B_N) があります。あなたは数列 A に対して次の操作を繰り返し行うことができます。
整数 i (1 ≦ i ≦ N – 1) を選ぶ。そして A_i を A_i xor A_i+1 に置き換えるか、A_i+1 を A_i xor A_i+1 に置き換えるかのいずれかを行う。ただし,xor はビットごとの排他的論理和を表す。
この操作を繰り返すことで,A と B を一致させることができるかを判定してください。
入力されるデータ
N
A_1 A_2 … A_N
B_1 B_2 … B_N(ただし、1 ≦ N ≦ 100,000
A_i, B_i は整数
0 ≦ A_i ≦ 2 60 – 1
0 ≦ B_i ≦ 2 60 – 1 )
実は行列の掃き出し法と同じです。各 A_i を二進法で表してそれを 0-1 ベクトル (行ベクトル) だと思うと、数列 A1, A2, …, AN は、N × 60 の行列になります。
これに「A_i を A_i xor A_i+1 に置き換える」は 行列の i 行目に i+1 行目を (XOR の意味で) 加算していることになります。2 つの整数列の双方から生成される行列 A, Bに
A の i 行目と j 行目とを交換する
A の j 行目を i 行目に (XOR の意味で) 加算する
という処理を繰り返す掃き出し法の処理をおこない両者が一致するかどうかを調べればよいということになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Gauss(long[] A) { int rank = 0; for (int d = 0; d < 60; d++) { int pivot = -1; for (int i = rank; i < A.Length; i++) { if (((A[i] >> d) & 1) == 1) { pivot = i; break; } } if (pivot == -1) continue; long copy = A[rank]; A[rank] = A[pivot]; A[pivot] = copy; for (int j = 0; j< A.Length; j++) { if (j == rank) continue; if (((A[j] >> d) & 1) != 1) continue; A[j] ^= A[rank]; } rank++; } } static void Main() { int N = int.Parse(Console.ReadLine()); long[] A = Console.ReadLine().Split().Select(_ => long.Parse(_)).ToArray(); long[] B = Console.ReadLine().Split().Select(_ => long.Parse(_)).ToArray(); Gauss(A); Gauss(B); bool ok = true; for (int i = 0; i < N; i++) { if (A[i] - B[i] != 0) ok = false; } if(ok) Console.WriteLine("Yes"); else Console.WriteLine("No"); } } |
