行列のかけ算は以下のように定義されています。
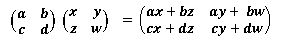
なぜこんなヘンテコな計算をするのでしょうか?
Contents
連立一次方程式を解く
行列は、図形の拡大、縮小、回転、鏡像などを計算するのに利用できます。また連立一次方程式にも使えます。以下のような連立方程式があったとします。
x + 2y = 3
4x + 5y = 6
これは行列を使うと以下のように書くことができます。
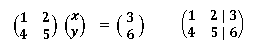
連立一次方程式の係数を並べた行列を係数行列と呼び、これに右辺の値を合体させた行列を拡大係数行列と呼びます。これを変形させて以下のような形に変化させれば方程式を解いたことになります。

掃き出し法は、ある行列に対して行の基本変形を繰り返し行い、階段行列に変形する際に利用する一連の操作のことです。
行の基本変形とは行列の基本変形とは、①行を入れ替える、②ある行を0ではない定数で定数倍すること、③ある行に他の行の定数倍を加えることです。行を入れ替えると連立方程式としては以下のようになります。
行を入れ替える前
x + 2y = 3
4x + 5y = 6
行を入れ替えた後
4x + 5y = 6
x + 2y = 3
連立方程式としてはなにも変化していません。
ある行を0ではない定数で定数することも
定数倍する前
x + 2y = 3
定数倍(この場合は2倍)した後
2x + 4y = 6
これも式としてはなにも変化していません。
ある行に他の行の定数倍を加えることとは
操作前
x + 2y = 3
4x + 5y = 6
下の式に上の式を-4倍したものを加えようとしている
x + 2y = 3
4x + 5y + (-4)(x + 2y) = 6 + (-4)×3
下の式に上の式を-4倍したものを加えたあと
x + 2y = 3
-3y = -6
これは加減法と同じ操作であることがわかります。
実際に拡大係数行列に対して基本変形をおこない、解を求めてみることにします。
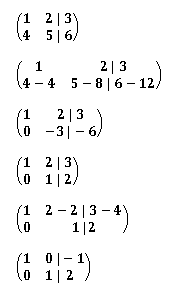
最初に下の行に上の行を-4倍したものを加え、そのあと下の行に3分の1を掛けています。そのあと上の行に下の行を-2倍したものを加えることで、x = -1, y = 2 という解を求めることができました。
ではコードを書いてみましょう。
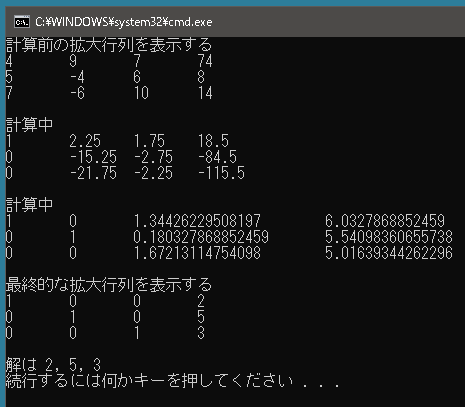
以下のコードでは三元連立方程式
4x + 9y + 7z = 74
5x – 4y + 6z = 8
7x – 6y + 10z = 14
の解を求めています。解だけでなく、拡大係数行列がどのように変化していくかも表示させています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { double[,] augmentedMatrix = { {4, 9, 7, 74,}, {5, -4, 6, 8,}, {7, -6, 10, 14,}, }; Console.WriteLine("計算前の拡大行列を表示する"); ShowAugmentedMatrix(augmentedMatrix); int rowMax = augmentedMatrix.GetLength(0); int colMax = augmentedMatrix.GetLength(1); bool isIndefiniteOrImmeasurable = false; for (int row = 0; row < rowMax; row++) { double coefficient = augmentedMatrix[row, row]; // 係数が0だった場合、それより下にある係数が0でない行を探す // 見つかったら行を入れ替える。見つからない場合は不定形または不能形 if (coefficient == 0) { for (int anotherRow = row + 1; anotherRow < rowMax; anotherRow++) { // 係数が0でない行がみつかったので行を入れ替える if (augmentedMatrix[anotherRow, row] != 0) { for (int col = 0; col < colMax; col++) { double d = augmentedMatrix[anotherRow, col]; augmentedMatrix[anotherRow, col] = augmentedMatrix[row, col]; augmentedMatrix[row, col] = d; } break; } } coefficient = augmentedMatrix[row, row]; if (coefficient == 0) { // 係数が0ではない行は見つからない場合は不定形または不能形。処理を終了する isIndefiniteOrImmeasurable = true; break; } } for (int col = 0; col < colMax; col++) augmentedMatrix[row, col] /= coefficient; for (int otherRow = 0; otherRow < rowMax; otherRow++) { if (otherRow == row) continue; double ratio = augmentedMatrix[otherRow, row]; for (int col = 0; col < colMax; col++) augmentedMatrix[otherRow, col] -= ratio * augmentedMatrix[row, col]; } if (row < rowMax - 1) Console.WriteLine("計算中"); else Console.WriteLine("最終的な拡大行列を表示する"); ShowAugmentedMatrix(augmentedMatrix); } if (!isIndefiniteOrImmeasurable) { List<double> solution = new List<double>(); for (int row = 0; row < rowMax; row++) solution.Add(augmentedMatrix[row, rowMax]); Console.WriteLine("解は " + string.Join(", ", solution)); } else Console.WriteLine("不定形または不能形です"); } static void ShowAugmentedMatrix(double[,] matrix) { for (int row = 0; row < matrix.GetLength(0); row++) { List<double> doubles = new List<double>(); for (int col = 0; col < matrix.GetLength(1); col++) { doubles.Add(matrix[row, col]); } Console.WriteLine(String.Join(" \t", doubles)); } Console.WriteLine(); } } |
実行結果
逆行列を求める
逆行列も以下のような拡張行列で求めます。最初は右側を単位行列にしておき、左側が単位行列になるように基本変形を繰り返します。このとき右側が逆行列となります。
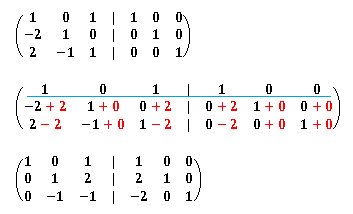
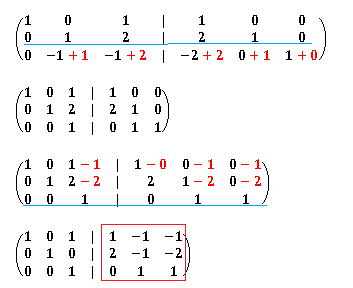
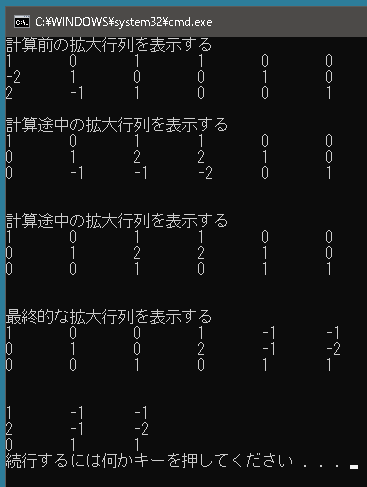
以下のコードでは

の逆行列を求めています。解だけでなく、拡大係数行列がどのように変化していくかも表示させています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
public class Program { static void Main() { double[,] matrix = { {1, 0, 1}, {-2, 1, 0}, {2, -1, 1}, }; double[,] augmentedMatrix = new double[matrix.GetLength(0), matrix.GetLength(1) * 2]; for (int row = 0; row < matrix.GetLength(0); row++) { for (int col = 0; col < matrix.GetLength(1); col++) augmentedMatrix[row, col] = matrix[row, col]; for (int col = 0; col < matrix.GetLength(1); col++) { if (col == row) augmentedMatrix[row, matrix.GetLength(1) + col] = 1; } } Console.WriteLine("計算前の拡大行列を表示する"); ShowAugmentedMatrix(augmentedMatrix); int rowMax = augmentedMatrix.GetLength(0); int colMax = augmentedMatrix.GetLength(1); bool isExistis = true; for (int row = 0; row < rowMax; row++) { double coefficient = augmentedMatrix[row, row]; if (coefficient == 0) { isExistis = false; break; } for (int col = 0; col < colMax; col++) { augmentedMatrix[row, col] /= coefficient; } for (int otherRow = 0; otherRow < rowMax; otherRow++) { if (otherRow == row) continue; double ratio = augmentedMatrix[otherRow, row]; for (int col = 0; col < colMax; col++) augmentedMatrix[otherRow, col] -= ratio * augmentedMatrix[row, col]; } if (row < rowMax - 1) Console.WriteLine("計算途中の拡大行列を表示する"); else Console.WriteLine("最終的な拡大行列を表示する"); ShowAugmentedMatrix(augmentedMatrix); } if (isExistis) { for (int row = 0; row < augmentedMatrix.GetLength(0); row++) { List<double> doubles = new List<double>(); for (int col = augmentedMatrix.GetLength(1) / 2; col < augmentedMatrix.GetLength(1); col++) doubles.Add(augmentedMatrix[row, col]); Console.WriteLine(String.Join(" \t", doubles)); } } else { Console.WriteLine("逆行列は存在しない"); } } } |
実行結果
行列式の計算
行列式とは正方行列に対して定義される量です。「式」という文字がついていますが方程式のようなものではなくスカラーです。つまり「1」とか「3」のような値をとります。
行列式には以下のような性質があります。
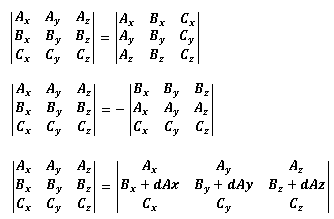
行と列を入れ替えても行列式は同じ。
ふたつの行を入れ替えると符号が反転する。
ある行の定数倍を別の行に加えても行列式は同じ。
行列式の1つの行(または列)の各要素に定数をかけた行列式の値は、もとの行列式の値の定数倍になる。
余因子展開
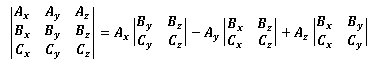
Ax, Ay, Azのどれかが0だと計算が簡単になります。ある行の定数倍を別の行に加えても行列式は同じという性質を使えばAx, Ay, Azのうちひとつを除いて0にすることができます。もしすべてが0の場合は行列式は0になります。
以下のコードでは

の行列式を求めています。
ここではおもにある行の定数倍を別の行に加えても行列式は同じであるという性質と余因子展開を用いて行数を減らすことで行列式を求めます。1×1の行列になったら処理は終了です。余因子展開を用いて行数を減っていく様子も表示させています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 |
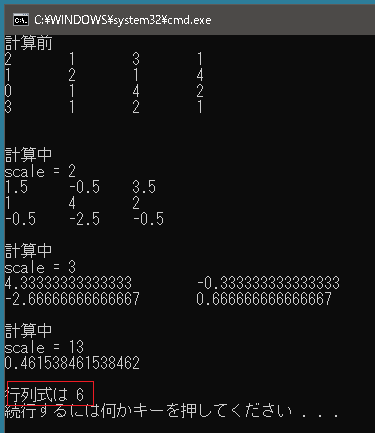
public class Program { static void Main() { double[,] matrix = { {2, 1, 3, 1,}, {1, 2, 1, 4,}, {0, 1, 4, 2,}, {3, 1, 2, 1,}, }; int rowMax = matrix.GetLength(0); int colMax = matrix.GetLength(1); double[,] matrix2 = new double[rowMax, colMax]; for (int row = 0; row < rowMax; row++) { for (int col = 0; col < colMax; col++) matrix2[row, col] = matrix[row, col]; } Console.WriteLine("計算前"); ShowMatrix(matrix2); double scale = 1; while (true) { rowMax = matrix2.GetLength(0); colMax = matrix2.GetLength(1); if (rowMax == 1) break; double leftTop = matrix2[0, 0]; if (leftTop != 0) scale *= leftTop; else { for (int row = 0; row < rowMax; row++) { if (matrix2[row, 0] != 0) { for (int col = 0; col < colMax; col++) { double d = matrix2[0, col]; matrix2[0, col] = matrix2[row, col]; matrix2[row, col] = d; } break; } } leftTop = matrix2[0, 0]; if (leftTop != 0) scale *= -leftTop; else { scale = 0; break; } } for (int col = 0; col < colMax; col++) matrix2[0, col] /= leftTop; for (int row = 1; row < rowMax; row++) { double d = matrix2[row, 0]; for (int col = 0; col < colMax; col++) matrix2[row, col] -= matrix2[0, col] * d; } double[,] submatrix = new double[rowMax - 1, colMax - 1]; for (int row = 1; row < rowMax; row++) { for (int col = 1; col < colMax; col++) submatrix[row - 1, col - 1] = matrix2[row, col]; } matrix2 = submatrix; Console.WriteLine("計算中"); Console.WriteLine("scale = " + scale); ShowMatrix(submatrix); } Console.WriteLine("行列式は " + matrix2[0, 0] * scale); } static void ShowMatrix(double[,] matrix) { for (int row = 0; row < matrix.GetLength(0); row++) { List<double> doubles = new List<double>(); for (int col = 0; col < matrix.GetLength(1); col++) { doubles.Add(matrix[row, col]); } Console.WriteLine(String.Join(" \t", doubles)); } Console.WriteLine(); } } |
実行結果