ひとりで勝手にはじめた蟻本読書会 平面・空間を扱う計算幾何 蟻本読書会 の続きです。
選択肢が無限にある最適化問題の場合、ギリギリを考えることで候補を有限個に絞るという方法があります。
White Bird (AOJ 2308)
鳥は原点から初期速度Vで任意の方向に飛ばすことができます。鳥は初期位置から放物線状の軌道を描き、途中で卵爆弾を垂直に落とすことができます。ただし鳥は障害物にぶつかると、卵爆弾を落とせなくなります。また卵爆弾は障害物に衝突すると消滅します。
障害物は辺が座標軸に平行な長方形で全部でN個存在します。重力加速度は9.8m/s^2です。
豚が座標 (X, Y)に存在します。鳥は卵爆弾を豚に命中させることはできるでしょうか?
入力されるデータ
N V X Y
l_1 b_1 r_1 t_1
l_2 b_2 r_2 t_2
…
l_N b_N r_N t_Nただし、
N : 障害物の数 ( 0 ≦ N ≦ 50 )
V : 白い鳥の初速度 ( 0 ≦ V ≦ 50 )
X, Y : 豚の位置 ( 0 ≦ X, Y ≦ 300 )
l_i: i番目の障害物の左側の x 座標
b_i: i番目の障害物の下側の y 座標
r_i: i番目の障害物の右側の x 座標
t_i: i番目の障害物の上側の y 座標
( 0 ≦ l_i, b_i, r_i, t_i ≦ 300 )l_i、b_i、r_i、t_i の値が 10 の-6乗だけ変更されても解は変化しないことが保証されています。
豚に卵爆弾をぶつけることができる条件は以下の2つを満たすときです。
① 鳥が障害物にぶつかることなく豚の真上まで移動することができる
② 豚の真上と豚とのあいだに障害物がない
問題では「鳥は原点から初期速度Vで任意の方向に」飛ばすことができるため、考えなければならない「鳥を射出する角度」は無限に存在するように思えるのですが、ここではふたつの場合だけ考えます。
① 鳥を直接豚に当てる場合
② ある障害物の左上と右上を通る場合
もし卵爆弾を豚に命中させることができるのであれば、① または ② は必ず存在します。これによって考えなければならない無限に存在する鳥の飛行コースを有限個に限定することができます。
calcメソッドは vy で射出した鳥が t 秒後に存在する高さを取得します。cmpメソッドは lb と ub に対する相対的な位置を取得します。checkメソッドは、qx, qy を通るように射出された鳥が豚に卵爆弾を命中させられるかを判定するためのものです。
checkメソッドの先頭部分で、初速が vx, vy で t 秒後に qx, qy を通るとすれば、t, vx, vy の値はどうなるかを計算しています。
vx と vy は初速の x 成分と y 成分なので vx ^ vx + vy ^ vy = V * V です。また x 成分の初速が vx で t 秒後には qx なので qx = vx * t です。それから y 成分の初速が vy で t 秒後には qy なので qy = vy * t – 0.5 * g * t * t です。なので以下のような連立方程式を解くことになります。
vx * vx + vy * vy = V * V … ①
qx = vx * t … ②
qy = vy * t – 0.5 * g * t * t … ③
これは ② を変形すると vx = qx / t, ③ を変形すると vy = qy / t + 0.5 * g * t, これを ① に代入すると qx / t
これは ① を変形すると vx * vx * t * t + vy * vy * t * t = V * V * t * t, ② を変形すると vx * t = qx, ③ を変形すると vy * t = qy + 0.5 * g * t * t, これを ① に代入すると
qx * qx + (qy + 0.5 * g * t * t) * (qy + 0.5 * g * t * t) = V * V * t * t
t * t = T とすると qx * qx + (qy + 0.5 * g * T) * (qy + 0.5 * g * T) = V * V * T となり、T の二次式として整理すると
(g * g / 4) * T * T + (g * qy – V * V) * T + (qx * qx + qy * qy) = 0
となります。このとき T は実数解を持たないといけないので
a = g * g / 4;
b = g * qy – V * V;
c = qx * qx + qy * qy;
とすると D = b * b – 4 * a * c ≧ 0(D は判別式)でなければなりません。D ≧ 0 の場合は T の値から t, vx, vy の値を求めます。
t, vx, vy の値から鳥の X 座標が豚の X 座標と一致したときの鳥の Y 座標がわかります。鳥の高さが豚の高さより低いなら卵をぶつけることはできません。また投下地点と豚のあいだに障害物がある場合も卵をぶつけることはできません。そして鳥が豚の真上に移動するまえに障害物にぶつかってしまう場合も卵をぶつけることはできません。これは鳥の X 座標が障害物の左右と一致したときに鳥の Y 座標がその障害物の上下の Y 座標のあいだにあるかどうか、鳥の Y 座標が障害物の上下と一致したときに鳥の X 座標がその障害物の左右の X 座標のあいだにあるかどうかを調べればわかります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 |
using System; using System.Collections.Generic; using System.Linq; class Program { static double g = 9.8; static double EPS = Math.Pow(10, -6); static int N, V, X, Y; static int[] L; static int[] B; static int[] R; static int[] T; static void Main() { { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; V = vs[1]; X = vs[2]; Y = vs[3]; } L = new int[N]; B = new int[N]; R = new int[N]; T = new int[N]; for (int i = 0; i < N; i++) R[i] = Math.Min(R[i], X); for (int i = 0; i < N; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); L[i] = vs[0]; B[i] = vs[1]; R[i] = vs[2]; T[i] = vs[3]; } bool ok = check(X, Y); for (int i = 0; i < N; i++) { ok |= check(L[i], T[i]); ok |= check(R[i], T[i]); } if(ok) Console.WriteLine("Yes"); else Console.WriteLine("No"); } static double calc(double vy, double t) { return vy * t - g * t * t / 2; } static int cmp(double lb, double ub, double a) { return a < lb + EPS ? -1 : a > ub - EPS ? 1 : 0; } static bool check(double qx, double qy) { // 初速が vx, vy で t 秒後に qx, qy を通るとすれば、t, vx, vy の値は? double a = g * g / 4; double b = g * qy - V * V; double c = qx * qx + qy * qy; double D = b * b - 4 * a * c; // 判別式 D が負数でも -EPS より大きければ 0 とみなす if (D < 0 && D > -EPS) D = 0; // 判別式 D が負数のときは t 秒後に qx, qy を通すための t は存在しない if (D < 0) return false; // 二次方程式を解く。解は 2 つあるのでそれぞれを考える for (int d = -1; d <= 1; d += 2) { double t2 = (-b + d * Math.Sqrt(D)) / (2 * a); if (t2 <= 0) // t * t が負数なら t は存在しない continue; double t = Math.Sqrt(t2); // t を求め、ここから vx と vy を求める double vx = qx / t; double vy = (qy + g * t * t / 2) / t; double yt = calc(vy, X / vx); // 鳥の X 座標が豚の X 座標と一致したときの鳥の Y 座標 if (yt < Y - EPS) // 鳥の高さが豚の高さより低いなら卵をぶつけることはできない continue; // 豚の真上から卵を落とせば命中させることができるか? bool ok = true; for (int i = 0; i < N; i++) { // 障害物は豚のX座標より向こう側にあるので問題外 if (L[i] >= X) continue; // 投下地点と豚のあいだに障害物があるのでできない if (R[i] == X && Y <= T[i] && B[i] <= yt) ok = false; // 豚の真上に移動するまえに鳥は障害物にぶつからないか? // 鳥と障害物の相対的な位置から考察する int yL = cmp(B[i], T[i], calc(vy, L[i] / vx)); int yR = cmp(B[i], T[i], calc(vy, R[i] / vx)); int xH = cmp(L[i], R[i], vx * (vy / g)); int yH = cmp(B[i], T[i], calc(vy, vy / g)); if (xH == 0 && yH >= 0 && yL < 0) ok = false; if (yL * yR <= 0) ok = false; } if (ok) return true; } return false; } } |
AOJ 1133 Circle and Points
xy平面上にN個の点が与えられる。半径1の円をxy平面 上で動かして、それらの点をなるべくたくさん囲むようにする。このとき最大でいくつの点を同時に囲めるかを答えなさい。ここである円が点を「囲む」 とは、その点が円の内部または円周上にあるときをいう。
二つの点の距離が 0.0001 より近くなることはない。一つのデータセット中の 任意の 2 点間の距離 d が 1.9999 ≦ d ≦ 2.0001を満たすことはない。また一つのデータセット中の任意の 3 点を P1, P2, P3 とし、xy 平面上のある点からそれぞれへの距離を d1, d2, d3 とする.このとき 0.9999 ≦ di ≦ 1.0001 (i = 1, 2, 3)が同時に成り立つことはない。
それぞれのデータセットに対して、データセット中の点で、半径 1 の円一つで同時に囲むことができる点の最大数を出力しなさい。
入力されるデータ
N1
x_1 y_1
x_2 y_2
…
x_N1 y_N1
N2
x_1 y_1
x_2 y_2
…
x_N2 y_N2
0(入力されるデータの最後は 0)(ただし、1 ≦ N ≦ 300
0.0 ≦ x_i, y_i ≦ 10.0 )
点を囲む半径 1 の円の中心は無数に存在するが、囲むことができる点の数を最大にしたいのであれば、探索対象を N 点のうち 2 点を通る円だけに限定しても解は変わりません。またある 2 点を通る円の中心は、その 2 点をそれぞれ中心とする円の交点となります。これだと円の組み合わせは N * (N – 1) / 2 とおりであり、円の交点は最大で N * (N – 1) 箇所になります。それらから距離 1 の点の数を数えるので、計算量は O(N ^ 3)となります。N は最大で 300 なので制限時間内に処理をおこなうことは可能です。
ある 2 点(a, b)と(c, d)を通る円の中心の座標を求めるにはどうすればよいでしょうか?
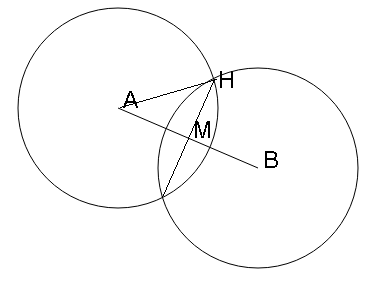
まず 2 点(A, B)を結ぶ直線の傾きと中点 M の座標を求めます。直線の傾きは(Yb – Ya)/ (Xb – Xa)であり、中点 M の座標は((Xa + Xb)/ 2, (Ya + Yb)/ 2)です。この中点を通り、この直線に直交する直線を求めます。ある直線の傾きとそれと直行する直線の傾きの積は -1 になるので、求めようとしている直線の傾きは (Xa – Xb)/(Yb – Ya)となります。
直角三角形を書くと MH の長さがわかります。AH は円の半径(半径は 1)なので、MH の長さは 1 – (A, B間の距離の半分)^2 の平方根となることがわかります。あとは三角関数を用いて H の座標を求めます。Math.Atan2メソッドを使えば X 軸に対する MH の角度(theta)がわかります。theta = Math.Atan2(Xa – Xb, Yb – Ya) です。そして theta を用いると 円の交点の座標は(Xa + Xb)/ 2 ± Math.Cos(theta), (Ya + Yb)/ 2) ± Math.Sin(theta) となります。
当然のことながら円の中心同士の距離が 2 を超えると円は交わることはできません。また問題文より円の中心同士の距離が 2 以下なのか以上なのかがはっきりしない微妙なものは存在しません。
円の交点の座標がわかったら、そこから距離 1 以内にある点の数を数えます。ただし誤差が発生するため注意が必要です。問題文には「任意の 3 点を P1, P2, P3 とし、xy 平面上のある点からそれぞれへの距離を d1, d2, d3 としたとき 0.9999 ≦ di ≦ 1.0001 が同時に成り立つことはない」とあります。そこで 距離 1 ではなく、距離 1.0001 以下のものを数えます。
円の交点が存在しない 2 点を選んでしまった場合、円で囲まれる点の数は 0 になります。しかし実際にはどのような場所に円を書いても必ず 1 つの点は円内に入ることができます。そこで点の個数を数える関数が 0 を返しそうになったときは 1 を返すようにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
using System; using System.Collections.Generic; using System.Linq; class Position { public Position(double x, double y) { X = x; Y = y; } public double X = 0; public double Y = 0; } class Program { static void Main() { List<int> rets = new List<int>(); while (true) { int N = int.Parse(Console.ReadLine()); if (N == 0) break; List<Position> positions = new List<Position>(); for (int i = 0; i < N; i++) { double[] vs = Console.ReadLine().Split().Select(_ => double.Parse(_)).ToArray(); positions.Add(new Position(vs[0], vs[1])); } rets.Add(Solve(N, positions)); } foreach(int ret in rets) Console.WriteLine(ret); } static int Solve(int N, List<Position> positions) { int ret =0; for (int i = 0; i < N; i++) { for (int k = i + 1; k < N; k++) { Position p1 = positions[i]; Position p2 = positions[k]; // 2 点を通る円の中心の座標を求める // 別の表現をすると、「2 点を中心とする円の交点の座標を求める」 double d = Math.Sqrt(Math.Pow(p1.X - p2.X, 2) + Math.Pow(p1.Y - p2.Y, 2)); if (d > 2) continue; // 2 点 が離れすぎしているので円は交差しない double xm = (p1.X + p2.X) / 2; double ym = (p1.Y + p2.Y) / 2; double h = Math.Sqrt(1 - Math.Pow(d / 2, 2)); double angle = Math.Atan2(p1.X - p2.X, p2.Y - p1.Y); // 円の交点の座標(x1, y1) double x1 = xm + h * Math.Cos(angle); double y1 = ym + h * Math.Sin(angle); ret = Math.Max(ret, GetCount(x1, y1, positions)); // 円の交点の座標(x2, y2) double x2 = xm - h * Math.Cos(angle); double y2 = ym - h * Math.Sin(angle); ret = Math.Max(ret, GetCount(x2, y2, positions)); } } // 0 を返しそうになったら 1 を返す if (ret == 0) ret = 1; return ret; } // positions内の(x, y)から距離 1 以内の点の数を返すメソッド static int GetCount(double x, double y, List<Position> positions) { int ret = 0; foreach (Position pos in positions) { double d = Math.Sqrt(Math.Pow(pos.X - x, 2) + Math.Pow(pos.Y - y, 2)); if (d <= 1.0001) // 問題文より想定される誤差 ret++; } return ret; } } |
