連続する部分列の総和を最大にする方法を考えます。
間違ってはいないが時間がかかる
まずは何の工夫もない方法から。二重ループですべての部分列の総和を計算してそのなかから最大値を求めようとしています。与えられた配列が短ければこれでも問題ないのですが、配列の長さが100,000を超えるようなものを渡されるといくら時間があっても終わりません。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int max = 0; for (int left = 0; left < vs.Length; left++) { for (int right = left; right < vs.Length; right++) { int sum = 0; for (int i = left; i <= right; i++) sum += vs[i]; if (max < sum_) max = sum; } } Console.WriteLine(max); } } |
累積和を利用する
配列Aが与えられたとき、配列Bを作り、B[0] = 0を代入します。それ以降はB[n] = A[0]~A[n – 1]までの総和を代入します。もし int[] A = { 1, 2, 3, 2, 1 }なら int[] B = {0, 1, 3, 6, 8, 9 }です。この段階で配列が1つ大きくなっています。
もし配列Aのa番目からb番目(先頭は0番目)を計算する必要があるときは B[b] – B[a – 1] を計算します。これで同じ区間を何度も足し算する必要はなくなりました。
累積和から部分列の総和の最大値を求める
つぎに連続する部分列の総和を最大にする方法を考えます。このときに部分列の開始と終了を二重ループで求めていては時間が足りません。ここはこのように考えます。
変数 M と max を0で初期化します。B[i] が M よりも小さいときはその値で M を更新します。そして B[i] – M の値が max よりも大きいときは max を更新します。最終的な max の値が「連続する部分列の総和の最大値」となります。
要は累積和 B を使うと[a, b]の総和は B[b+1] – B[a](ただし b >= a)となるので、B[a]が小さいときが候補になります。そこで B[a] の暫定的最小値 M を求め、B[i] – Mが最大になるときが求めるべき総和の最大値となるわけです。
また最大値だけでなくその区間がどこからどこまでなのかも知りたいときはMを更新するときにtempLeftに値を保存しておき、max を更新するときに tempLeft に 1 足した値と i で left と right を更新します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
static void Solve(int[] values) { int len = values.Length; int[] sums = new int[len + 1]; for (int i = 0; i < len; i++) sums[i + 1] += sums[i] + values[i]; int[] ms = new int[len + 1]; int[] maxs = new int[len + 1]; int[] tempLefts = new int[len + 1]; int[] tempRights = new int[len + 1]; List<string> strings = new List<string>(); tempLefts[0] = -1; tempRights[0] = -1; int left = -1; int right = -1; int max = 0; for (int i = 0; i < len; i++) { if (ms[i] >= sums[i + 1]) { ms[i + 1] = sums[i + 1]; tempLefts[i + 1] = i; } else { ms[i + 1] = ms[i]; tempLefts[i + 1] = tempLefts[i]; } if (maxs[i] < sums[i + 1] - ms[i + 1]) { maxs[i + 1] = sums[i + 1] - ms[i + 1]; tempRights[i + 1] = i; left = tempLefts[i + 1] + 1; right = tempRights[i + 1]; max = maxs[i + 1]; strings.Add($"更新:[{left}, {right}] が最大値 {max}"); } else { maxs[i + 1] = maxs[i]; tempRights[i + 1] = tempRights[i]; } } Console.WriteLine("An\t" + string.Join("\t", values)); Console.WriteLine("Sn\t" + string.Join("\t", sums)); Console.WriteLine("Mn\t" + string.Join("\t", ms)); Console.WriteLine("Maxn\t" + string.Join("\t", maxs)); Console.WriteLine("TempL\t" + string.Join("\t", tempLefts)); Console.WriteLine("TempR\t" + string.Join("\t", tempRights)); Console.WriteLine($"{string.Join("\n", strings)}"); Console.WriteLine($"[{left}, {right}] が最大値 {max}"); } |
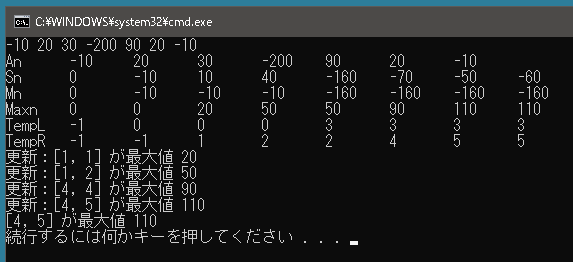
サンプルコードではデバッグ情報としていろいろ表示させましたが、実際には必要ないので以下のコードのほうがシンプルです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
public class Program { static void Main() { if (right != -1) Console.WriteLine($"[{left}, {right}] 最大値は {max}"); else Console.WriteLine($"部分列は空。最大値は {max}"); } static void GetMaxSpan(int[] values, ref int max, ref int left, ref int right) { left = -1; right = -1; max = 0; int len = values.Length; int[] sums = new int[len + 1]; for (int i = 0; i < len; i++) sums[i + 1] += sums[i] + values[i]; int m = 0; int tempLeft = -1; for (int i = 0; i < len; i++) { if (m >= sums[i + 1]) { m = sums[i + 1]; tempLeft = i; } if (max < sums[i + 1] - m) { max = sums[i + 1] - m; left = tempLeft + 1; right = i; } } } } |
連続する部分列の総和の最小値
連続する部分列の総和の最小値もこれで計算できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
public class Program { static void GetMinSpan(int[] values, ref long min, ref int left, ref int right) { left = -1; right = -1; min = 0; int len = values.Length; int[] sums = new int[len + 1]; for (int i = 0; i < len; i++) sums[i + 1] += sums[i] + values[i]; int m = 0; int tempLeft = -1; for (int i = 0; i < len; i++) { if (m <= sums[i + 1]) { m = sums[i + 1]; tempLeft = i; } if (min > sums[i + 1] - m) { min = sums[i + 1] - m; left = tempLeft + 1; right = i; } } } } |
