二分探索木は左の子孫の値 < 親の値 ≦ 右の子孫の値」という制約を持つ二分木です。直接下の左の子だけでなく左部分木のすべてのノードの値が親よりも小さくなる特性があります。右部分木のすべてのノードの値も同様に親以上になる特性があります
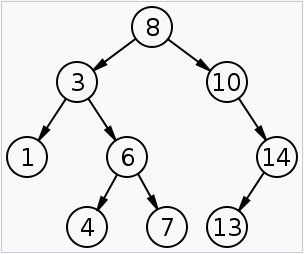
二分探索木ではそれぞれのノードに対し、左の子<ノードの値≦右の子が成り立つので、データの探索をするときに全探索をしなくても少ない回数の比較で探索をすることができます。
二分探索木をC#で実装してみる
二分探索木をC#で実装してみることにします。
以下のようなNodeクラスを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 |
public class Node { public Node(int key) { Key = key; } public int Key = 0; public Node Left = null; public Node Right = null; } |
挿入
ルートが存在しない場合は挿入しようとしているノードをルートノードとする。
ルートノードが存在する場合、ルートノードと目的の値を比較する。挿入しようとしている値のほうが着目しているノードより小さい場合は左の子、そうでないなら右の子が次の着目ノードとなる。
次の着目ノードが存在しなければその一にデータを挿入。存在する場合は次の着目ノードに移る・・・を繰り返す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
public class BinarySearchTree { public Node Root { private set; get; } public void Insert(int value) { Node node = new Node(value); if (Root == null) { Root = node; return; } Node cur = Root; while (true) { if (cur.Key > value) { if (cur.Left == null) { cur.Left = node; return; } cur = cur.Left; } else { if (cur.Right == null) { cur.Right = node; return; } cur = cur.Right; } } } } |
探索
二分探索木のなかに特定の値のデータがあるかどうかは以下の方法で調べることができます。
まずルートに着目する。
着目しているノードよりも目的の値が小さい場合は左の子、着目しているノードよりも目的の値が大きいなら右の子へ移る・・・を繰り返す。
着目しているノードと目的の値が等しい場合は「存在する」。着目ノードが存在しなければ「存在しない」として終了。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
public class BinarySearchTree { public bool Find(int target) { if (Root == null) return false; Node cur = Root; while (true) { if (cur.Key == target) return true; if (cur.Key < target) { if (cur.Right == null) return false; else cur = cur.Right; } if (cur.Key > target) { if (cur.Left == null) return false; else cur = cur.Left; } } } } |
全データの列挙
通りがけ順探索をすることで全データをソートされた順序で列挙できる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
public class BinarySearchTree { public List<Node> Sort() { List<Node> list = new List<Node>(); if (Root != null) DFS(Root); return list; void DFS(Node node) { if (node.Left != null) DFS(node.Left); list.Add(node); if (node.Right != null) DFS(node.Right); } } } |
削除
探索、挿入に比べると、削除の処理はちょっと複雑です。削除しても探索ができ、全データの列挙をしたときにソートされた状態で結果が取得できる状態を維持できるようにしなければなりません。
まず削除するノードがあるか確認する。ある場合は以下の場合分けをする
(1) 削除するノードには子が存在しない。
(2) 削除するノードには左または右のみ子が存在する。
(3) 削除するノードには左右の子が存在する。
(1)の場合は簡単です。そのまま削除します。
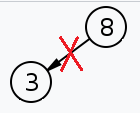
(2)の場合は削除して削除したノードの親と子をつなぎます。
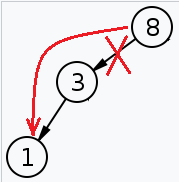
(3)の場合はさらに場合分けします。
(3a) 削除するノードの左の子に右の子が存在しない。
(3b) 削除するノードの左の子に右の子が存在する。
(3a)の場合は削除したノードの親と削除したノードの左の子をつなぎます。削除したノードの左の子の右の子を削除したノードの右の子にする。
長々とした変な文章ですが、図にするとこういうことです。
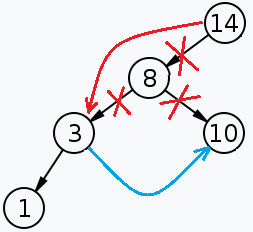
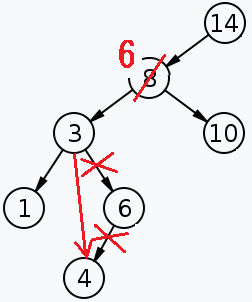
(3b) の場合
削除するノードの左の子から最大の値を探索する。これは右の子をたどり続けることで得られます。
これ(最大値ノード)を削除対象のノードと置き換える
最大値ノードの親の右の子を最大値ノードの左の子とする。
これも長々とした変な文章ですが、図にするとこういうことです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 |
public class BinarySearchTree { public bool Remove(int target) { // 削除対象は存在するか? Node targetParent = null; Node removeNode; // 削除対象の親ノード bool isLeft = false; // 削除対象は親の左の子か右の子か? if (Root == null) return false; Node cur = Root; while (true) { if (cur.Key == target) { removeNode = cur; break; } if (cur.Key > target) { if (cur.Left == null) return false; else { targetParent = cur; isLeft = true; cur = cur.Left; } } if (cur.Key < target) { if (cur.Right == null) return false; else { targetParent = cur; isLeft = false; cur = cur.Right; } } } // (1) 削除するノードには子が存在しない。 if (removeNode.Left == null && removeNode.Right == null) { if (targetParent != null) { if (isLeft) targetParent.Left = null; else targetParent.Right = null; } else Root = null; return true; } // (2) 削除するノードには左または右のみ子が存在する。 else if (removeNode.Left != null && removeNode.Right == null) { if (targetParent != null) { if (isLeft) targetParent.Left = removeNode.Left; else targetParent.Right = removeNode.Left; } else Root = removeNode.Left; return true; } else if (removeNode.Left == null && removeNode.Right != null) { if (targetParent != null) { if (isLeft) targetParent.Left = removeNode.Right; else targetParent.Right = removeNode.Right; } else Root = removeNode.Right; return true; } // (3a) 削除するノードの左の子に右の子が存在しない。 else if (removeNode.Left != null && removeNode.Right != null && removeNode.Left.Right == null) { if (targetParent != null) { if (isLeft) targetParent.Left = removeNode.Left; else targetParent.Right = removeNode.Left; removeNode.Left.Right = removeNode.Right; } else { Root = removeNode.Left; removeNode.Left.Right = removeNode.Right; } return true; } // (3b) それ以外のケース else { // 削除するノードの左の子から最大の値を探索する cur = removeNode.Left; Node maxParent = removeNode; while (true) { if (cur.Right != null) { maxParent = cur; cur = cur.Right; } else break; } // 最大値ノードを削除対象のノードと置き換える int max = cur.Key; removeNode.Key = max; // 最大値ノードの親の右の子を最大値ノードの左の子とする。 maxParent.Right = cur.Left; return true; } } } |
実際に使ってみる
定義したBinarySearchTreeクラスを使って二分探索木にデータを追加、削除、探索ができるアプリケーションを作成してみることにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
public class Program { static void Main() { BinarySearchTree bst = new BinarySearchTree(); while (true) { Console.WriteLine($"なにをしますか? a:追加 f:検索 r:削除 s:全データの列挙 e:終了"); string cmd = Console.ReadLine(); if (cmd == "a") { Console.WriteLine($"追加する値(int型)を入力してください"); int? n = ToInt(Console.ReadLine()); if (n != null) { bst.Insert((int)n); Console.WriteLine($"{n}を追加しました"); } else Console.WriteLine($"不正な入力です"); } else if (cmd == "r") { Console.WriteLine($"削除する値を入力してください"); int? n = ToInt(Console.ReadLine()); if (n != null) { if (bst.Remove((int)n)) Console.WriteLine($"{n}を削除しました"); else Console.WriteLine($"{n}は存在しないので削除できません"); } else Console.WriteLine($"不正な入力です"); } else if (cmd == "f") { Console.WriteLine("何を探しますか?"); int? n = ToInt(Console.ReadLine()); if (n != null) { if (bst.Find((int)n)) Console.WriteLine($"{n}は存在します"); else Console.WriteLine($"{n}は存在しません"); } else Console.WriteLine($"不正な入力です"); } else if (cmd == "s") { List<Node> sorted = bst.Sort(); string[] strings = sorted.Select(_ => _.Key.ToString()).ToArray(); Console.WriteLine(string.Join(", ", strings)); } else if (cmd == "e") break; else Console.WriteLine("不正な入力です"); } Console.WriteLine("終了"); } static int? ToInt(string s) { try { return int.Parse(s); } catch { return null; } } } |
