ハノイの塔はアルゴリズムの定番問題です。3本の杭と、中央に穴の開いた大きさの異なる複数の円盤から構成され、最初はすべての円盤が左端の杭に小さいものが上になるように順に積み重ねられています。すべての円盤を右端の杭に移動させられれば完成ですが、一度に移動することができる円盤は一枚だけです。また小さな円盤の上に大きな円盤を乗せることはできません。
Contents
C# コンソールアプリ
まずC#でこれをやってみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static List<int>[] piles = new List<int>[3]; static long moveCount = 0; static int numberOfStages = 3; static void Main() { Init(numberOfStages); // 後述 ShowPiles(); // 後述 Hanoi(numberOfStages, 0, 2, 1); // 後述 } } |
塔の初期化
Initメソッドはハノイの塔の初期化をおこないます。配列に空のリストをセットして、一番左側の杭にあたるpiles[0]に{n, n-1, ……, 1}を格納します。
ハノイの塔では小さな円盤の上に大きな円盤を乗せることはできないというルールがあります。1~nの整数が円盤の大きさになっていて、先に格納されている値が下に存在する円盤にあたります。そのため値は大きい順に格納されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
public class Program { static void Init(int n) { piles[0] = new List<int>(); piles[1] = new List<int>(); piles[2] = new List<int>(); for (int i = n; i > 0; i--) piles[0].Add(i); } } |
塔の状態を表示する
ShowPilesメソッドは各杭にある円盤の番号を表示します。
|
1 2 3 4 5 6 7 8 9 10 |
public class Program { static void ShowPiles() { Console.WriteLine("----"); // 区切りの線 Console.WriteLine($"count:{moveCount}"); // 何回目の移動が終了した状態なのか? for (int i = 0; i < piles.Length; i++) Console.WriteLine($"{i}:{string.Join(" ", piles[i])}"); } } |
円盤を移動させる処理
円盤を移動させる処理を示します。piles[from]の一番最後の要素を取り除き、piles[to]の一番最後に追加しているだけです。
|
1 2 3 4 5 6 7 8 9 10 11 |
public class Program { static void MoveOne(int from, int to) { int last = piles[from][piles[from].Count - 1]; piles[from].RemoveAt(piles[from].Count - 1); piles[to].Add(last); moveCount++; ShowPiles(); } } |
再帰で複数の円盤を移動させる
移動させるためにはまず一番下にあるもの以外を動かしたい杭ではない杭に移動させます。そして一番下にある円盤を移動させたい杭の位置に移動させて、事前に移動してあった他の円盤をその上に移動させます。では図の場合、1~3はどうやって移動させればよいでしょうか? 1と2を空いている別の杭に移動させてから3を移動させればよいのです。1と2を移動させるためには1を別の杭に移動させることで2を移動できるようになります。
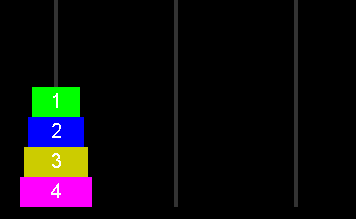
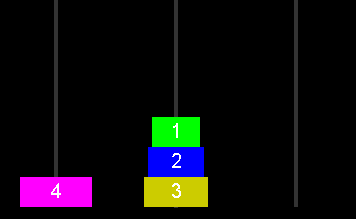
このように考えると再帰処理をすればよいことがわかります。Hanoiメソッドのなかでnを1減らして再帰呼び出しをして、そのあとMoveOneメソッドで一番下にある円盤を移動させたあと、いったん待避させておいた円盤をその上に移動させます。そのため移動の処理の回数はnが1増えるにしたがって前回の2倍+1回ということになります。
漸化式 A(1) = 1, A(n+1) = 2A(n) + 1 を解くとA(n) = 2^n – 1となることがわかります。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
public class Program { static void Hanoi(int n, int from, int to, int temp) { if (n == 0) return; Hanoi(n - 1, from, temp, to); MoveOne(from, to); Hanoi(n - 1, temp, to, from); } } |
実行結果
実行結果は以下のようになります。A(n) = 2^n – 1なので塔が3段の場合は7回の動作で移動させることができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
---- count:0 0:3 2 1 1: 2: ---- count:1 0:3 2 1: 2:1 ---- count:2 0:3 1:2 2:1 ---- count:3 0:3 1:2 1 2: ---- count:4 0: 1:2 1 2:3 ---- count:5 0:1 1:2 2:3 ---- count:6 0:1 1: 2:3 2 ---- count:7 0: 1: 2:3 2 1 |
特定のステップの状態を表示する
次に塔の高さと回数が与えられたら現在の状態を表示できるようにします。A(n) = 2^n – 1なのでnが少し大きな数になると処理が爆発的に増えてしまいます。例えば塔が64段で638億4000万回(西暦元年に1秒に1枚移動する処理を開始したとするとだいたいこの回数になる)移動したときどのような状態になっているか調べようとする場合、プログラムを改良しないと時間がいくらあっても終わりません。
変更部分だけ示します。まずフィールド変数としてtargetとdoneを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
public class Program { static List<int>[] piles = new List<int>[3]; static long moveCount = 0; static int numberOfStages = 64; static long target = 63840000000; static bool done = false; // 全部移動するのではなく結果が出たら終わらせる static void Main() { Init(numberOfStages); ShowPiles(); Hanoi(numberOfStages, 0, 2, 1); } } |
doneがtrueの場合は結果が取得できたあとなので以降はMoveOneメソッドとHanoiメソッドのなかではなにもしません。ShowPilesメソッドを実行するのはmoveCount == targetのときだけです。
n枚を移動させるためにはMath.Pow(2, n) – 1回の処理が必要ですが、HanoiメソッドのなかではmoveCount + Math.Pow(2, n) – 1 <= targetである場合、再帰処理はしないで直接移動処理をしています。またその場合はmoveCountにMath.Pow(2, n) - 1を加算しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
public class Program { static void MoveOne(int from, int to) { if (done) return; int last = piles[from][piles[from].Count - 1]; piles[from].RemoveAt(piles[from].Count - 1); piles[to].Add(last); moveCount++; if (moveCount == target) { ShowPiles(); done = true; } } static void Hanoi(int n, int from, int to, int temp) { if (n == 0 || done) return; if (moveCount + Math.Pow(2, n) - 1 <= target) { // まとめて移動させたとしても移動回数がtargetを超えない場合はまとめて移動する List<int> disks = piles[from].Skip(piles[from].Count - n).ToList(); piles[from] = piles[from].Take(piles[from].Count - n).ToList(); piles[to].AddRange(disks); moveCount += (int)Math.Pow(2, n) - 1; } else { // まとめて移動させると移動回数がtargetを超える場合はこれまでどおりの再帰処理をする Hanoi(n - 1, from, temp, to); MoveOne(from, to); Hanoi(n - 1, temp, to, from); } } } |
実行結果はこうなります。
|
1 2 3 4 |
count:63840000000 0:64 63 62 61 60 59 58 57 56 55 54 53 52 51 50 49 48 47 46 45 44 43 42 41 34 29 28 27 24 23 20 17 1:39 38 35 32 31 26 21 16 15 14 11 10 9 8 7 6 5 4 3 2 1 2:40 37 36 33 30 25 22 19 18 13 12 |
西暦元年から移動処理を開始していたとしても半分どころか41番~64番までまったく手つかずであることがわかります。
インドのガンジス河の畔のヴァラナシに、世界の中心を表すという巨大な寺院がある。そこには青銅の板の上に、長さ1キュビット、太さが蜂の体ほどの3本のダイヤモンドの針が立てられている。そのうちの1本には、天地創造のときに神が64枚の純金の円盤を大きい円盤から順に重ねて置いた。これが「ブラフマーの塔」である。司祭たちはそこで、昼夜を通して円盤を別の柱に移し替えている。そして、全ての円盤の移し替えが終わったときに、世界は崩壊し終焉を迎える。
とのことですが、64段のハノイの塔を実際に動かす場合は、2^64-1回(約1844京6744兆回)となり、これは1回を1秒で動かすとして約5845億年もかかります。世界が滅亡するのはまだまだ先のことなので心配はなさそうです。
JavaScriptでもやってみる
JavaScriptでもやってみることにします。これは塔が10段の場合、どのような移動がおこなわれるかシミュレーションできます。また表示速度も変更できるようにします。
HTML部分
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
<!DOCTYPE html> <html lang="ja"> <head> <meta charset="UTF-8"> <title>ハノイの塔 シミュレーション</title> <meta name = "viewport" content = "width=device-width, initial-scale = 1.0"> <style> h1 { font-size: 20px;} #canvas { display: block; margin-bottom: 10px; } .button { width: 100px; height: 30px; } #cancel { display: none; } </style> </head> <body> <h1>ハノイの塔 シミュレーション</h1> <div id = "result"></div> <canvas id = "canvas"></canvas> <div id = "interval-outer">間隔(ミリ秒 100-3000):<input type="number" id = "interval" value="1000" min="100" max="3000" step="10"></div> <button id = "run" class="button" onclick="run()">実行</button> <button id = "cancel" class="button" onclick="cancel()">キャンセル</button> <script src= "./index.js"></script> </body> </html> |
グローバル変数と定数
index.js
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
const numberOfStages = 10; // 塔は10段 const piles = []; let moveCount = 0; let canceling = false; // 処理が途中で中断された let interval = 1000; // 最初は1秒に1枚移動 const CANVAS_WIDTH = 360; const CANVAS_HEIGHT = 360; const pileCenterXs = [CANVAS_WIDTH / 2 - 120, CANVAS_WIDTH / 2, CANVAS_WIDTH / 2 + 120]; // 杭のX座標 // 円盤に色をつける const colors = ['#f00','#0f0','#00f','#cc0','#f0f','#0ff','#800','#080','#008','#880','#808','#088',]; // canvas要素とコンテキスト const $canvas = document.getElementById('canvas'); const ctx = $canvas.getContext('2d'); // ボタン要素など const $run = document.getElementById('run'); const $cancel = document.getElementById('cancel'); const $intervalOuter = document.getElementById('interval-outer'); const $interval = document.getElementById('interval'); |
ページが読み込まれたときの処理
ページが読み込まれたときの処理を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
window.onload = async() => { $canvas.width = CANVAS_WIDTH; $canvas.height = CANVAS_HEIGHT; ctx.fillStyle='#000'; ctx.fillRect(0, 0, CANVAS_WIDTH, CANVAS_HEIGHT); piles[0] = []; piles[1] = []; piles[2] = []; for (let i = numberOfStages; i > 0; i--) piles[0].push(i); showPiles(); // 後述 } |
杭の状態を表示する関数を示します。ここでは文字情報だけでなく視覚的にもわかるようにそれぞれの円盤をcanvasに描画しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
function showPiles(){ let text = ''; text += `count:${moveCount}<br>`; for (let i = 0; i < piles.length; i++) text += `${i}:${piles[i].join(' ')}<br>`; document.getElementById('result').innerHTML = text; // canvasをクリア ctx.fillStyle='#000'; ctx.fillRect(0, 0, CANVAS_WIDTH, CANVAS_HEIGHT); // 杭の描画 ctx.fillStyle='#333'; ctx.fillRect(pileCenterXs[0] - 2, 0, 4, CANVAS_HEIGHT); ctx.fillRect(pileCenterXs[1] - 2, 0, 4, CANVAS_HEIGHT); ctx.fillRect(pileCenterXs[2] - 2, 0, 4, CANVAS_HEIGHT); // 円盤の描画 for(let i=0; i<piles.length; i++){ for(let k=0; k<piles[i].length; k++) showDisk(piles[i][k], k, i); } } |
円盤を描画する関数を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
function showDisk(deskNum, deskIndex, pileNum){ // 円盤を矩形で描画 ctx.fillStyle=colors[deskNum % colors.length] const thickness = 30; const width = 80 - (5-deskNum) * 8; const y = CANVAS_HEIGHT - thickness * (deskIndex + 1); ctx.fillRect(pileCenterXs[pileNum], y, width/2, thickness); ctx.fillRect(pileCenterXs[pileNum] - width/2, y, width/2, thickness); // 円盤の番号も描画する ctx.textBaseline = 'top'; ctx.font = '20px Arial'; ctx.fillStyle='#fff'; const textWidth = ctx.measureText(deskNum).width; ctx.fillText(deskNum, pileCenterXs[pileNum] - textWidth / 2, y + 5); } |
円盤を移動させる
円盤を移動させる関数を示します。配列の最後の要素を取り出して移動先の配列の最後に追加しています。そして自作関数のsleepを呼び出してintervalだけ待機しています。
|
1 2 3 4 5 6 7 8 9 10 11 |
async function moveOne(from, to){ if(canceling) // キャンセルボタンが押されたらなにもしない return; const last = piles[from].pop(); piles[to].push(last); moveCount++; await sleep(interval); showPiles(); } |
待機処理をする関数を示します。
|
1 2 3 |
async function sleep(ms){ return await new Promise(resolve => setTimeout(resolve, ms)); } |
hanoi関数は再帰処理で引数分の個数の円盤を移動させる関数です。
|
1 2 3 4 5 6 7 8 |
async function hanoi(n, from, to, temp){ if (n == 0 || canceling) // キャンセルボタンが押されたらなにもしない return; await hanoi(n - 1, from, temp, to); await moveOne(from, to); await hanoi(n - 1, temp, to, from); } |
シミュレーションを開始する
[実行]ボタンをクリックしたらシミュレーションを開始します。その処理を示します。
実行中は[実行]ボタンを非表示にしてキャンセル用のボタンを表示させます。1回1回の移動の間隔をどれだけ開けるかはテキストボックスから取得します。取得された値がminとmaxのあいだであればその値をintervalに格納し、不適切な値の場合はminかmaxの値を採用します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
async function run(){ $run.style.display = 'none'; $intervalOuter.style.display = 'none'; $cancel.style.display = 'block'; // intervalはどうするか? const min = Number($interval.min); const max = Number($interval.max); const value = Number($interval.value); if(min <= value && value <= max) interval = value; else if(min > value) interval = min; else if(max < value) interval = max; $interval.value = interval; // 塔を初期化 moveCount = 0; piles[0] = []; piles[1] = []; piles[2] = []; for (let i = numberOfStages; i > 0; i--) piles[0].push(i); // 移動処理開始、終わるまで待機 await hanoi(numberOfStages, 0, 2, 1); // 処理が終わったら[実行]ボタンを表示させ、キャンセル用のボタンを非表示にする $run.style.display = 'block'; $intervalOuter.style.display = 'block'; $cancel.style.display = 'none'; canceling = false; // キャンセル処理中のフラグをクリア } |
シミュレーションをキャンセルしようとしたときの処理を示します。cancelingフラグをセットすることでhanoi関数とmoveOne関数がなにもしないで処理を返すのでシミュレーションの処理も終了します。
|
1 2 3 |
function cancel(){ canceling = true; } |
