C# JavaScript 不規則な形をした図形との当たり判定ではCrossing Number アルゴリズムを用いて点と多角形の内外判定をしました。この方法は「多角形の各線分ごとに指定した点を通るx軸に平行な線との交点があるかどうかを調べ、交点が指定した点より右にあればカウントする。カウントした点が奇数なら指定した点は多角形に含まれている」というものでした。今回はWinding Number アルゴリズムで同じような処理を実装します。
Winding Number アルゴリズム
Winding Number アルゴリズムは以下のような内容です。
点Pを多角形の内部にあるかどうかを調べたい点、点Pと各頂点とを結ぶ辺を L[0]…L[n](ただしL[n] = L[0])とします。L[i]とL[i+1]とが成す角の符号付き角度を求めてその総和を計算します。
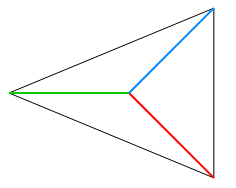
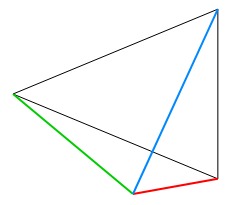
図からわかるように点Pが多角形の内部にあると符号付き角度(この場合は赤と青、青と緑、緑と赤のそれぞれ間の角度)の総和は360度になります。
点Pが多角形の外部にあると符号付き角度の総和は0度になります。この場合、かならず符号付き角度の符号が逆になってしまうものができてしまうのです(赤と青、青と緑に対して、緑と赤の間の角度は逆周りになっている)。
ベクトルの内積と外積から符号付き角度を求める
では符号付き角度はどのようにして求めればよいでしょうか?
まず2つのベクトルの符号付きではない角度ですが、ベクトルの内積を使うことで求めることができます。ベクトルの内積は Ax * Bx + Ay * By で求めることができるし、|A| * |B| * cosθで求めることもできます。この2つの公式から内積を求め、cosの逆関数でθを求めることができます。ただAとBを入れ替えても内積の符号はかわりません。cosθとcos(-θ)は同じ値だからです。
では符号付きの角度を求めるにはどうすればよいでしょうか? ベクトルの外積を使います。
3次元ベクトル A(Ax, Ay, Az) と B(Bx, By, Bz) の外積の公式を使うと A と B の外積 C = A × B の Cz は Ax * By – Ay * Bx になるのでこれを使います。Cz が負数になるときは内積を用いて得たθの符号を反転させます。
あとは得られたθの総和を計算するだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
// points には多角形の座標が格納されている // pt は 多角形の内部にあるかどうか調べたい点の座標 bool Check(Point[] points, Point pt) { double sum = 0; for (int i = 0; i < points.Length - 1; i++) sum += GetAngle(points[i + 1].X - pt.X, points[i + 1].Y - pt.Y, points[i].X - pt.X, points[i].Y - pt.Y); sum += GetAngle(points[0].X - pt.X, points[0].Y - pt.Y, points.Last().X - pt.X, points.Last().Y - pt.Y); return Math.Round(sum / Math.PI / 2) != 0; double GetAngle(int vx1, int vy1, int vx2, int vy2) { double innerProduct = (vx1 * vx2 + vy1 * vy2) / Math.Sqrt(vx1 * vx1 + vy1 * vy1) / Math.Sqrt(vx2 * vx2 + vy2 * vy2); double ret = Math.Acos(innerProduct); if (vx1 * vy2 - vx2 * vy1 < 0) ret *= -1; return ret; } } |
またこの方法は凸多角形だけでなく凹多角形(角度が180度より大きい内角を持つ多角形)や自己交差がある多角形(辺同士が交わる多角形)でも内外判定をすることができます。
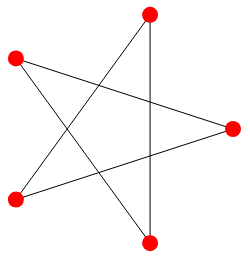
自己交差がある多角形の例(頂点をむすぶ辺同士が交差している)
