巡回セールスマン問題を最近傍法で解く
巡回セールスマン問題を最近傍法で解いてみることにします。やり方は以下のとおり。
始点となる都市を適当に1つ選ぶ。これが今いる都市。
今までに訪れたことのない都市のうち、今いる都市に最も近い都市を訪れる
すべての都市を訪れるまで、これを繰り返す
このアルゴリズムはある程度良い解が出力されることが期待される方法ではありますが、解の精度はまったく保証されません。
都市の座標を管理するためのNodeクラスを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
using System; using System.Collections.Generic; using System.Linq; public class Node { public Node(int x, int y) { X = x; Y = y; } public int X = 0; public int Y = 0; } |
最近傍法で巡回セールスマン問題を解くクラスを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
public class NearestNeighbor { public List<int> GetSolution(Node[] nodes, ref double d) { int count = nodes.Length; bool[] isVisits = new bool[count]; // 0番都市からスタート int current = 0; List<int> paths = new List<int>(); paths.Add(0); while (true) { double distance2 = double.MaxValue; // 暫定的な最小値を格納する変数 int candidate = -1; // 候補 isVisits[current] = true; for (int i = 0; i < count; i++) { if (i == current || isVisits[i]) continue; // 処理にかかる時間を短縮するために距離ではなく距離の2乗を比較する double d2 = Math.Pow(nodes[i].X - nodes[current].X, 2) + Math.Pow(nodes[i].Y - nodes[current].Y, 2); if (distance2 > d2) { distance2 = d2; candidate = i; } } current = candidate; // candidateが更新されない(未訪問の都市は存在しない)場合は終了 if (candidate == -1) break; paths.Add(candidate); } // 最短距離を計算する double totalDistance = 0; for (int i = 0; i < paths.Count; i++) { int from = paths[i]; int to; if (i + 1 < paths.Count) to = paths[i + 1]; else to = 0; double d2 = Math.Pow(nodes[to].X - nodes[from].X, 2) + Math.Pow(nodes[to].Y - nodes[from].Y, 2); totalDistance += Math.Sqrt(d2); } d = totalDistance; return paths; } } |
実際に都市の座標を適当に設定して処理をおこなわせてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
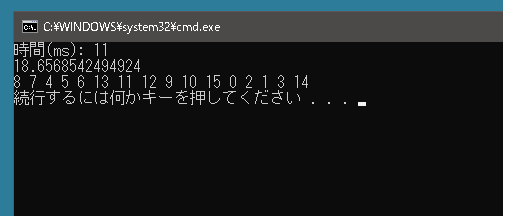
public class Program { static void Main() { List<Node> nodes = new List<Node>() { new Node(2, 0), new Node(1, 1), new Node(2, 1), new Node(1, 2), new Node(0, 0), new Node(-1, 0), new Node(-2, 0), new Node(-1, 1), new Node(-1, 2), new Node(1, -2), new Node(2, -2), new Node(-1, -2), new Node(0, -2), new Node(-1, -1), new Node(2, 2), new Node(1, -1), }; System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); double d = 0; NearestNeighbor neighbor = new NearestNeighbor(); List<int> ret = neighbor.GetSolution(nodes.ToArray(), ref d); stopwatch.Stop(); Console.WriteLine($"時間(ms): {stopwatch.ElapsedMilliseconds}"); Console.WriteLine(d); Console.WriteLine(string.Join(" ", ret.ToArray())); } } |
前回の動的計画法を使った場合よりも処理速度は速いです。都市の数が5000件あっても1~2秒で終わります。ただ正確な値を得られていません。
巡回セールスマン問題を貪欲法で解く
巡回セールスマン問題を貪欲法で解いてみることにします。やり方は以下のとおり。
各都市同士の距離を計算して近い順に連結する。
ただし
ふたつ以上の都市と連結させない。
閉路ができないようにする。
これによって全都市は一本のパスでつながることになる。最後に始点と終点を繋いげば巡回路が得られる
最初に都市の座標を管理するためのNodeクラスを定義します。
都市を近い順に連結していくのですが、3つ以上の都市が連結されたり閉路ができないようにしなければなりません。フィールド変数 ConnectCountは自分と連結している都市の数が格納されます。
閉路ができないようにするためには都市を連結するときに片方を親にします。親をもつ都市同士を連結するときは双方の親を比較します。親が同じだと閉路ができてしまうことになります。親が異なる場合は連結させるとともに、片方の親がもう片方の親の子になります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
using System; using System.Collections.Generic; using System.Linq; public class Node { static int _no = 0; Node _parentNode; public int X = 0; public int Y = 0; public int ConnectCount = 0; public int NodeNumber = 0; public Node(int x, int y) { X = x; Y = y; _parentNode = this; NodeNumber = _no; _no++; } public void SetParent(Node node) { _parentNode = node; } public Node GetParentNode() { if(_parentNode == this) return this; Node parent = this._parentNode; while (true) { Node parent2 = parent._parentNode; if (parent2 == parent) return parent; parent = parent2; } } } |
Edgeクラスのコンストラクタの引数は異なる2つの都市です。コンストラクタ内で距離を計算してフィールド変数に格納します。
Joinメソッドはすでにふたつ以上の都市が連結しているときや、都市の親が同じ場合はなにもしません。それ以外のときは連結します。連結する場合はConnectCountをインクリメントするとともに片方の都市の親をもう片方の親の子にセットします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
public class Edge { public double Distance = 0; public Node Node1 = null; public Node Node2 = null; public Edge(Node node1, Node node2) { Node1 = node1; Node2 = node2; double d2 = Math.Pow(node2.X - node1.X, 2) + Math.Pow(node2.Y - node1.Y, 2); Distance = Math.Sqrt(d2); } public bool Join() { if (Node1.ConnectCount == 2 || Node2.ConnectCount == 2) return false; if (Node1.GetParentNode() == Node2.GetParentNode()) return false; Node1.GetParentNode().SetParent(Node2.GetParentNode()); Node1.ConnectCount++; Node2.ConnectCount++; return true; } } |
上記のアルゴリズムで最短経路を求めるためのクラスを定義します。戻り値は最短経路で第二引数が最短距離を受け取る変数です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
public class Greedy { public List<int> GetSolution(Node[] nodes, ref double d) { int n = nodes.Length; List<Edge> edges = new List<Edge>(); for (int a = 0; a < n; a++) { for (int b = 0; b < n; b++) { if (a >= b) continue; // 引数のNode.NodeNumberが小さいものを第一引数にする Edge edge = new Edge(nodes[a], nodes[b]); edges.Add(edge); } } edges = edges.OrderBy(_ => _.Distance).ToList(); // 距離が小さい順にソート List<Edge> joinedEdges = new List<Edge>(); foreach (Edge edge in edges) { // 連結することができるなら連結し、エッジをリストに格納する if (edge.Join()) joinedEdges.Add(edge); } // スタートする都市を探す(ConnectCountが1の都市がふたつあるので片方を選択する) Node startNode = nodes.FirstOrDefault(_ => _.ConnectCount == 1); Node cur = startNode; List<int> path = new List<int>(); path.Add(cur.NodeNumber); while (true) { // 両端にcurがあるエッジを探す。 // 見つかったらそのエッジのもう片方の都市を取得してそれを両端にもつエッジを探す。 // 同じエッジを選んでしまわないように見つけたエッジはjoinedEdgesから削除する。 Edge curEdge1 = joinedEdges.FirstOrDefault(_ => _.Node1 == cur); if (curEdge1 != null) { joinedEdges.Remove(curEdge1); cur = curEdge1.Node2; path.Add(cur.NodeNumber); continue; } Edge curEdge2 = joinedEdges.FirstOrDefault(_ => _.Node2 == cur); if (curEdge2 != null) { joinedEdges.Remove(curEdge2); cur = curEdge2.Node1; path.Add(cur.NodeNumber); continue; } break; } // 最短距離を計算する double totalDistance = 0; for (int i = 0; i < path.Count; i++) { int from = path[i]; int to; if (i + 1 < path.Count) to = path[i + 1]; else to = 0; double d2 = Math.Pow(nodes[to].X - nodes[from].X, 2) + Math.Pow(nodes[to].Y - nodes[from].Y, 2); totalDistance += Math.Sqrt(d2); } d = totalDistance; return path; } } |
実際に都市の座標を適当に設定して処理をおこなわせてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
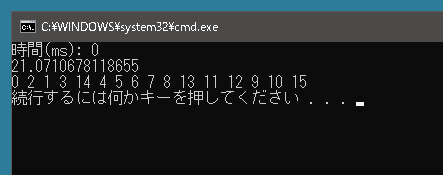
public class Program { static void Main() { List<Node> nodes = new List<Node>() { new Node(2, 0), new Node(1, 1), new Node(2, 1), new Node(1, 2), new Node(0, 0), new Node(-1, 0), new Node(-2, 0), new Node(-1, 1), new Node(-1, 2), new Node(1, -2), new Node(2, -2), new Node(-1, -2), new Node(0, -2), new Node(-1, -1), new Node(2, 2), new Node(1, -1), }; System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); double d = 0; Greedy greedy = new Greedy(); List<int> ret = greedy.GetSolution(nodes.ToArray(), ref d); stopwatch.Stop(); Console.WriteLine($"時間(ms): {stopwatch.ElapsedMilliseconds}"); Console.WriteLine(d); Console.WriteLine(string.Join(" ", ret.ToArray())); } } |
最近傍法と比べると処理時間がかかります。ただし動的計画法を使った場合よりも処理速度は速いです。都市の数が3000件でも3秒近くかかります。また得られるのは正確な値ではありません。