巡回セールスマン問題とは、都市の集合と各都市間の距離が与えられ、全都市をちょうど1回ずつ訪れたのち出発した都市に戻ってくるような経路 (巡回路) のうち最も短いものを求める問題です。
どのようにして解を求めればよいのでしょうか? 一番最初に思いつくのが総当たり法です。
都市は全部で4つあり、それぞれの名前を A, B, C, Dとすれば、都市Aを最初に訪問する方法だけでも
|
|
A, B, C, D A, B, D, C A, C, B, D A, C, D, B A, D, B, C A, D, C, B |
と6通りあります。都市が全部で4つある場合は全部で24通り考えなければなりません。都市が全部でn個あるのであれば、n × (n – 1) × (n – 2) × (n – 3) × …… × 2 × 1通りです。nが1増えるたびにそのパターンの数は爆発的に増えていきます。そこで別の方法を考えます。
都市が16以下であれば動的計画法
nが16以下であれば動的計画法が有効です。
ある都市 s からスタートし、集合 S に含まれるすべての都市を訪れ、都市 j に到達する最短路を p(j, S)、その長さを d(j, S) と表記します。都市の集合 S をビット列による表現を用いて表しています。
まず簡単にわかることとしてd(j, {j})があります。このとき集合の要素は j だけです。なのでd(j, {j})は都市 s から都市 j までの距離です。
次に、p(j, S) において j の直前に訪れる頂点を i とします。すると、p(j, S) の頂点 i に到達するまでの部分路は、都市 s からスタートして集合 S – {j} に含まれるすべての都市を訪れ、頂点 i に到達する最短路になっているはずです。従って、d(j, S) は d(i, S – {j}) + (都市 i から都市 j までの距離) の最小値となりです。
集合演算をするにあたりビット演算を用います。集合 S のなかに i番目の都市があるかどうかは S & (1<
|
|
using System; using System.Collections.Generic; public class Position { public Position(int x, int y) { X = x; Y = y; } public int X = 0; public int Y = 0; } |
動的計画法で巡回セールスマン問題を解くためのクラスを定義します。GetDistanceメソッドは都市間の距離を求めるためのものです。GetSolutionメソッドに都市の座標を渡して処理をおこないます。このとき最短経路と処理にかかる時間も取得できるようにしておきます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
public class TSP_DP { double GetDistance(Position position1, Position position2) { double d2 = Math.Pow(position2.X - position1.X, 2) + Math.Pow(position2.Y - position1.Y, 2); return Math.Sqrt(d2); } public double GetSolution(Position[] positions, ref int[] path, ref long ms) { // 処理にかかる時間も計測する System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); int n = positions.Length; // d[i, b] (b は 集合S のビット列による表現) double[,] d = new double[n, 1 << n]; int[,] before = new int[n, 1 << n]; // 経路を保存する // d の初期化 for (int i = 0; i < n; i++) { for (int b = 0; b < 1 << n; b++) { d[i, b] = double.MaxValue; before[i, 1 << i] = 0; } } // 集合 S のサイズが 1 の場合(集合の要素はi番目の都市だけのとき) for (int i = 0; i < n; i++) d[i, 1 << i] = GetDistance(positions[0], positions[i]);// (都市 s から 都市 i への距離); // 集合のサイズを1つずつ大きくしていく for (int b = 0; b < 1 << n; b++) { for (int i = 0; i < n; i++) { if ((b >> i & 1) == 0) // 集合Sのなかにi番目の都市は存在しない continue; for (int j = 0; j < n; j++) { if ((b >> j & 1) == 1) continue; // 都市 i から都市 j への距離を計算して配列内の値と比較して小さければ更新する double tmp = d[i, b] + GetDistance(positions[i], positions[j]); if (tmp < d[j, b | (1 << j)]) { d[j, b | (1 << j)] = tmp; before[j, b | (1 << j)] = i; } } } } int[] tour = new int[n]; int pos = 0; int bit = (1 << n) - 1; for (int i = 0; i < n; i++) { tour[i] = before[pos, bit]; bit = bit ^ (1 << pos); pos = tour[i]; } // この時点で、tour は最小の巡回路長を達成する巡回路になっている path = tour; stopwatch.Stop(); ms = stopwatch.ElapsedMilliseconds; return d[0, (1 << n) - 1]; } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
public class Program { static void Main() { List<Position> positions = new List<Position>() { new Position(2, 0), new Position(1, 1), new Position(2, 1), new Position(1, 2), new Position(0, 0), new Position(-1, 0), new Position(-2, 0), new Position(-1, 1), new Position(-1, 2), new Position(1, -2), new Position(2, -2), new Position(-1, -2), new Position(0, -2), new Position(-1, -1), new Position(2, 2), new Position(1, -1), }; TSP_DP tSP_DP = new TSP_DP(); int[] path = null; long ms = 0; double ret = tSP_DP.GetSolution(positions.ToArray(), ref path, ref ms); Console.WriteLine($"時間(ms): {ms}"); Console.WriteLine(ret); Console.WriteLine(string.Join(" ", path)); } } |
実行結果
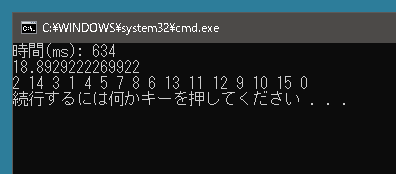
この方法だと1秒以内に終わります。
(参考)【paizaラーニング】動的計画法によるTSP

