平方分割で区間の最大値を求める大量のクエリに対応するの続きです。前回は最初に整数の配列が与えられましたが、その配列の値が更新されることはありませんでした。今回はある区間の最大値を求める + ある区間で配列の値が更新される が同時におこなわれるような問題を考えます。
Long Bricksを解く
たとえばこんな問題です。
W 個の正方形のマスが左右に並んだ水平な部分があります。最初、すべての部分について、高さは 0 です。ここに高さ 1 のレンガを N 個、順番に積みます。高さ h の面に接着したレンガの上面の高さは h+1 になります。
i 番目に積むレンガは、左から L_i 番目から R_i 番目のマスをちょうど覆うように置きます。このとき、レンガが覆う範囲の中で最も高い水平な面で接着します。各レンガについて、上面の高さを求めてください。
入力される値
W N
L_1 R_1
L_2 R_2
L_3 R_3L_N R_N
ただし
2 ≦ W ≦ 500,000
1 ≦ N ≦ 250,000
1 ≦ L_i ≦ R_i ≦ W
レンガは以下のような形で置かれていくわけですね。
もし、W = 18, N = 5
L[i] と R[i] がぞれぞれ
3 11
7 15
5 9
13 18
3 5
だったとするとレンガは以下のように置かれます。答えは 1,2,3,3,4 となります。
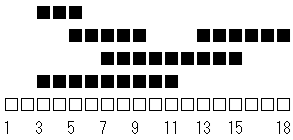
ではどのように考えればよいでしょうか? 最初は閉区間 [3, 11] で高さの最大値を考えます。最初はレンガはひとつも置かれていないので 0 です。レンガを置くことで高さが 1 上昇します。レンガの上面は平らなので閉区間 [3, 11] すべての高さを 1 に変更します。
次は閉区間 [7, 15] で高さの最大値を考えます。この場合、高さの最大値は 1 です。レンガを置くことで高さが 1 上昇します。レンガの上面は平らなので閉区間 [3, 11] の高さはこの最大値に1を加えた 2 にすべて変更されます。
これは指定された区間の最大値の取得と指定された区間の値を更新(すべてに同じ数を足すのではなくすべて同じ値に変更する)するという大量のクエリに高速で対応せよという問題です。
平方分割で解く
前回の問題とちがって W は平方数であるという保証はされていません。それでも平方分割は使えます。ただ「W は平方数でない」場合、あることを見落とすとその恩恵にあずかれないかもしれません。
どうでもいい話かもしれませんが、漢字で書くなら「恩恵に与る」または「恩恵に関る」であり「預かる」ではないみたいです。
配列内のある区間の最大値は前回の記事 平方分割で区間の最大値を求める大量のクエリに対応する の方法で取得することができました。今回は最大値の取得だけでなく区間をある値で更新する処理もおこなわなければなりません。もちろん大きなまとまった要素にひとつひとつ値をセットするなんてことはしません。2 ≦ W ≦ 500,000, 1 ≦ N ≦ 250,000という制約があるので、こんなことをやっていては間に合いません。
平方分割の遅延伝搬
ではどうするのか?
まずは長さ W の配列 A を定義します。ここには各マスの高さが入ります。最初はレンガはひとつも置かれていないので、A の要素はすべて 0 です。そして W の平方根を切り上げた数を root とすれば A は長さ root の配列に分割されます。ただし最後の配列は root より短くなるかもしれません。
平方分割した区間全体の値を更新する場合は配列に直接値をセットするのではなく、別の配列(ここでは lazyUpdates という名前にする)に格納します。平方分割した配列が大きい場合、かなりの時間短縮が期待できます。範囲をはみ出した部分は配列 A の値をそのまま変更します。
lazyUpdates配列に値をいれた状態では A[i] の値は実際の各マスの高さを違っているのでどこかで同期する必要があります。これは可能なかぎり先延ばしにします。
これ以上動機を先延ばしにできない場合とはどのような場合でしょうか? それは平方分割した区間全体に同じ値がセットされないような更新がされようとした場合です。また区間の最大値も平方分割した区間全体の値が更新されるのであれば同時に1回だけ変更してしまえばいいのですが、そうでない場合は個別に同期が必要です。
たとえば 長さ16の配列があったとすれば平方分割で長さ4の配列4つに分割できます。最大値を格納する配列 rangeMaxes と 更新する値を格納する lazyUpdates の長さはそれぞれ 4 となります。A のなかにある / は4つずつの区切りをわかりやすくするためのもので、わり算の記号ではありません。
|
1 2 3 |
A: {0, 0, 0, 0, / 0, 0, 0, 0, / 0, 0, 0, 0, / 0, 0, 0, 0} rangeMaxes: {0, 0, 0, 0} lazyUpdates: {0, 0, 0, 0} |
A[3] ~ A[13] の値をすべて 1 にするというのであれば、以下のようにします。A[4] ~ A[11]はそのままです。かわりに lazyUpdates[1] と lazyUpdates[2] を変更します。また区間全体が同じ値に更新されるので、その区間の最大値もその値と同じ値になります。なので rangeMaxes[1] と rangeMaxes[2] も同じ値に変更されます。
|
1 2 3 |
A: {0, 0, 0, 1, / 0, 0, 0, 0, / 0, 0, 0, 0, / 1, 1, 0, 0} rangeMaxes: {0, 1, 1, 0} lazyUpdates: {0, 1, 1, 0} |
そのあと A[2] ~ A[12] の最大値を知りたいのであれば A[2] A[3] A[7] A[12] rangeMaxes[1] rangeMaxes[2]の値をなかから最大値を探せばよいのでした。これは前回の記事のとおりです。
次に A[2] ~ A[12] をすべて 2 にするのであればこうなります。
|
1 2 3 |
A: {0, 0, 2, 2, / 0, 0, 0, 0, / 0, 0, 0, 0, / 2, 1, 0, 0} rangeMaxes: {0, 2, 2, 0} lazyUpdates: {0, 2, 2, 0} |
ここまでは動機を先延ばしにしても問題ありません。
では A[6] ~ A[12] をすべて 3 にしようとする場合はどうなるでしょうか?
|
1 2 3 |
A: {0, 0, 2, 2, / 0, 0, 3, 3, / 0, 0, 0, 0, / 3, 1, 0, 0} rangeMaxes: {0, 3, 3, 0} lazyUpdates: {0, 3, 3, 0} |
これではいけません。A[4] と A[5] の値は実は 2 なのですが、そのことが完全にわからなくなってしまいました。値の変更を区間まるごとおこなうことができない場合はlazyUpdatesの値を伝搬させる遅延伝搬の処理が必要です。遅延伝搬をさせるには区間のすべての要素にその値をセットするだけです。そしてその部分に対応するlazyUpdatesの要素は 0 にリセットします。
|
1 2 3 |
A: {0, 0, 2, 2, / 0, 0, 0, 0, / 0, 0, 0, 0, / 2, 1, 0, 0} rangeMaxes: {0, 2, 2, 0} lazyUpdates: {0, 2, 2, 0} |
ここから A[6] ~ A[12] をすべて 3 に変更するのであれば lazyUpdates[2] はそのままでよいのですが、lazyUpdates[1]の値は伝搬させなければなりません。そこで、まずはこうなります。伝搬させただけで値の更新はまだやっていません。
|
1 2 3 |
A: {0, 0, 2, 2, / 2, 2, 2, 2, / 0, 0, 0, 0, / 2, 1, 0, 0} rangeMaxes: {0, 2, 2, 0} lazyUpdates: {0, 0, 2, 0} |
伝搬の処理が終わったので値を更新します。
|
1 2 3 |
A: {0, 0, 2, 2, / 2, 2, 3, 3, / 0, 0, 0, 0, / 3, 1, 0, 0} rangeMaxes: {0, 3, 3, 0} lazyUpdates: {0, 0, 3, 0} |
つぎに A[9] ~ A[10] の最大値を計算せよというクエリが飛んできたらどうすればよいでしょうか? この場合は 9 ~ 10 が rangeMaxes[2]の範囲を完全にカバーしていないので(A[8] と A[11]の部分がはみ出している)ので、実際に A[9] ~ A[10] までを調べて最大値を返さなければならないのですが、それをするためには伝搬処理が必要です。伝搬処理をすると以下のようになります。
|
1 2 3 |
A: {0, 0, 2, 2, / 2, 2, 3, 3, / 3, 3, 3, 3, / 3, 1, 0, 0} rangeMaxes: {0, 3, 3, 0} lazyUpdates: {0, 0, 0, 0} |
このあと A[9] ~ A[10] の最大値を調べて返します。
このように伝搬させる必要がない処理は可能な限り引き伸ばして、本当に必要な部分だけ伝搬処理をすることができれば、区間の値の更新と最大値、総和を計算するクエリが大量に飛んできても対応することができるようになるのです。
コードを書く
以下のようなコードを書いてみました。あることを見落としていてなかなかテストが通りませんできたが、なんとか通すことができました。見落としていたのはコード内のコメントの③の部分です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { // 入力される W と N の値を取得する int W, N; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); W = vs[0]; N = vs[1]; } // マスは全部で W 個あるのでその高さを格納する配列を定義する int[] A = new int[W]; // 平方分割の処理に必要な変数と配列(区間の最大値と遅延伝搬用の配列) int root = (int)Math.Ceiling(Math.Sqrt(W)); int[] rangeMaxes = new int[root]; int[] lazyUpdates = new int[root]; // i 番目に乗せたレンガの高さを問われているので結果を格納するリストを定義する List<int> rets = new List<int>(); for (int i = 0; i < N; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int left = vs[0] - 1; // 配列の添字は0からに対し、入力は1からになっているので調整する int right = vs[1] - 1; int max = 0; // 閉区間 [left, right] の最大の高さは? int cur = left; while (cur <= right) { // 区間をleftから順番にrightまでみていく // そのときひとつひとつ調べずにrangeMaxesの値が使えるなら // それを使うことで計算量を減らす // rangeMaxesの値が使える場合とは ① かつ(②または③)の場合 // ① cur が平方分割された配列の開始点である // ② 終了点と同じ場所かその向こう側に right が存在する場合 // ③ right が配列 A の最後である場合(これを見落とすと通らないテストケースがある) int rangeIndex = cur / root; int case0 = 0; if (cur % root == 0) { if (cur + root - 1 <= right) case0 = 1; else if (right == A.Length - 1) case0 = 2; } if (case0 == 1 || case0 == 2) { max = Math.Max(max, rangeMaxes[rangeIndex]); if (case0 == 1) cur += root; if (case0 == 2) break; } else { // 条件にあてはまらない場合はひとつひとつ調べる // この際、対応する部分のlazyUpdatesに0以外の値が格納されていたら // 遅延伝搬の処理が必要である if (lazyUpdates[rangeIndex] != 0) { int start = rangeIndex * root; int end = (rangeIndex + 1) * root - 1; if (end > A.Length - 1) end = A.Length - 1; for (int index = start; index <= end; index++) A[index] = lazyUpdates[rangeIndex]; lazyUpdates[rangeIndex] = 0; } // 遅延伝搬の処理がおわったら最大値の計算をする max = Math.Max(max, A[cur]); cur++; } } // 得られた最大値より1大きい値がつぎに積まれたレンガの頂上の高さである int newValue = max + 1; cur = left; while (cur <= right) { // 上記の ① かつ(②または③)の場合は lazyUpdates を使う // そうでない場合は 配列 A に直接値をセットする int rangeIndex = cur / root; int case0 = 0; if (cur % root == 0) { if (cur + root - 1 <= right) case0 = 1; else if (right == A.Length - 1) case0 = 2; } if (case0 == 1 || case0 == 2) { lazyUpdates[rangeIndex] = newValue; rangeMaxes[rangeIndex] = newValue; if (case0 == 1) cur += root; if (case0 == 2) break; } else { // A[cur] に値をセットするまえに遅延伝搬の処理が必要になる場合がある // 上記の最大値を取得する範囲と値を更新する範囲が完全に同じなので // すでに遅延伝搬の処理はおこなわれているので省略している A[cur] = newValue; rangeMaxes[rangeIndex] = Math.Max(rangeMaxes[rangeIndex], newValue); cur++; } } rets.Add(newValue); } foreach (int i in rets) Console.WriteLine(i); } } |
やっと通った。