JavaScriptで上海麻雀をつくるの続きです。今回は上海麻雀の感想戦モードを実装します。
Contents
判定方法について
上海麻雀の感想戦モードでは牌を取ったときにゲームクリア可能なのか詰みパターンに入っているのかがリアルタイムでわかるようにします。そのためには現在の状態がゲームクリア可能なのか詰みパターンなのかを判定できなければなりません。
詰み形とは?
「詰み形」を以下のように定義します。
「詰み確定形」とは「すべての牌をとることができていないにもかかわらず次に取ることができる牌が存在しない形」のことである。
「詰み確定形」の各段各行の一番端にある選択できる牌を「ブロッキング牌」と定義する。
「詰み必至形」とは「詰み確定形」に「ブロッキング牌」以外の牌を追加した形である。この形からはいくつかの牌を取り除くことはできるが、ブロッキング牌とその内側にある牌は絶対に取り除くことはできないので詰みを回避することはできない形とみなすことができる。
「詰み確定形」と「詰み必至形」をあわせて「詰み形」と呼ぶことにする。
バックトラック法
方法としては現在の状態からバックトラック法でゲームクリアできるかどうかを調べます。バックトラック法とは選択できる手のなかからひとつを選んで牌を取り続け、途中で牌を取ることができなくなったら直前の状態に戻って別のルートを探すという方法です。
クリア可能な筋がひとつでも存在するならゲームクリア可能だし、そのような筋がひとつも存在しないのであれば「詰み形」と判断してよいので、ここはバックトラック法で考えます。
2秒間待ってもダメなら「判定不能」
ただ実際にやってみるとほとんどの場合は結果を出すことができるのですが、ときどきいつまで待っても答えが帰ってこないことがあります。この原因は牌の配置パターンによっては考えなければならない場合の数が非常に多くなってしまうことにあります。
そこで 2秒間処理をおこなって結果がでない場合は「判定不能」と表示させることにします。また前の状態の判定結果が次の状態の判定結果に使える場合があるので、判定結果の再利用もすることで処理の高速化をはかります。
一度調べた状態を記憶する
牌を取る順番が違うだけで同じ状態になることがあります。そこで一度調べた状態は記憶しておき、何度も同じ状態からの探索はしないようにします。
具体的な方法は以下のとおりです。
(1)各段各行の一番左側にある牌の列番号と一番右側にある牌の列番号を配列にして保存しておく。
(2)探索をしたらこの配列に格納されている値と探索結果(クリア可能 or 詰み形)をセットにして保存する。
(3)この配列に格納されている値と保存されている配列の値がすべて同じであれば「一度探索した状態」と判断する。
(4)配列の内容をその都度保存していたら容量が大きくなり、検索にも時間がかかるので配列の値をTree構造に格納する。根から最後のノードまでたどることができたら「配列に格納されている値がすべて同じ」とみなす(Trie木みたいなもの)。
TrieTreeクラスとTrieNodeクラスの定義
Trie木とは以下のようなものです。これは文字列をあつかっています。次の文字でどのノードに移動するのかでTree構造を構築しているのですが、文字ではなく配列の各要素の値を使おうというわけです。
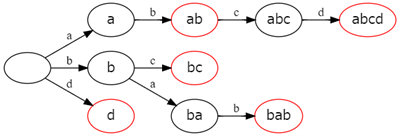
TrieNodeクラスを以下のように定義します。this.Resultは最後のノードに設定します。この値が 1 ならクリア可能、-1 なら詰み形、0 ならまだ判定できていない、または末尾のノードではないことを意味しています。
|
1 2 3 4 5 6 7 8 |
class TrieNode { constructor(){ this.Nexts = []; for(let i=0; i<=COL_COUNT;i++) this.Nexts[i] = null; this.Result = 0; // 0:判定まだ 1:クリア可能 -1:詰み形 } } |
TrieTreeクラスを以下のように定義します。Insert関数はふたつの配列(正確には「配列の配列」)と探索結果を登録します。Matching関数は引数で渡された「配列の配列」が登録されているのであれば結果(0:判定まだ 1:クリア可能 -1:詰み形)を返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
class TrieTree { constructor(){ this.Root = new TrieNode(); this.Count = 0; // 登録された件数(デバッグ用) } Insert(leftmostCols, rightmostCols, result){ let cur = this.Root; let add = false; for(let depth = 0; depth < DEPTH_COUNT; depth++){ for(let row = 0; row < ROW_COUNT; row++){ const number = leftmostCols[depth][row] + 1; if(cur.Nexts[number] == null){ cur.Nexts[number] = new TrieNode(); add = true; } cur = cur.Nexts[number]; } } for(let depth = 0; depth < DEPTH_COUNT; depth++){ for(let row = 0; row < ROW_COUNT; row++){ const number = rightmostCols[depth][row] + 1; if(cur.Nexts[number] == null){ cur.Nexts[number] = new TrieNode(); add = true; } cur = cur.Nexts[number]; } } cur.Result = result; if(add) this.Count++; } Matching(leftmostCols, rightmostCols){ let cur = this.Root; for(let depth = 0; depth < DEPTH_COUNT; depth++){ for(let row = 0; row < ROW_COUNT; row++){ const number = leftmostCols[depth][row] + 1; if(cur.Nexts[number] == null){ return 0; } cur = cur.Nexts[number]; } } for(let depth = 0; depth < DEPTH_COUNT; depth++){ for(let row = 0; row < ROW_COUNT; row++){ const number = rightmostCols[depth][row] + 1; if(cur.Nexts[number] == null){ return 0; } cur = cur.Nexts[number]; } } return cur.Result; } } |
CheckerStalemateCourseクラスの定義
CheckerStalemateCourseクラスは現在の状態が詰み形かどうかを判定するためのものです。
コンストラクタでTrie木とStalematePatterns配列を初期化しています。StalematePatterns配列には詰み確定形とブロッキング牌の番号の配列をセットにして格納します。ここから現在の状態が詰み必至形かどうか判定することができます。またこれは次回スタートボタンを押下されるまで格納されたデータを再利用できるのでメンバー変数にしています。
|
1 2 3 4 5 6 |
class CheckerStalemateCourse { constructor(){ this.SeenTrieTree = new TrieTree(); this.StalematePatterns = []; } } |
InitBeforeCheck関数は現在の状態が詰み形かどうかを判定するにあたって必要な準備をする処理をおこないます。
ここでやっていることは メンバ変数の配列 TileNumbers3x3 に各位置の牌の番号を格納することと、それらの左右の端にあたる列番号を格納する配列 LeftmostCols と RightmostCols の初期化と値の設定、残りの牌を数える変数 TilesCount への値の設定などです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
class CheckerStalemateCourse { InitBeforeCheck(tiles3x3){ this.TileNumbers3x3 = []; for(let depth = 0; depth < DEPTH_COUNT; depth++){ const arr1 = []; for(let row = 0; row < ROW_COUNT; row++){ const arr2 = []; for(let col = 0; col < COL_COUNT; col++) arr2.push(0); arr1.push(arr2); } this.TileNumbers3x3.push(arr1); } this.LeftmostCols = []; this.RightmostCols = []; for(let depth = 0; depth < DEPTH_COUNT; depth++){ this.LeftmostCols[depth] = []; this.RightmostCols[depth] = []; for(let row = 0; row < ROW_COUNT; row++){ this.LeftmostCols[depth][row] = -1; this.RightmostCols[depth][row] = -1; } } this.TilesCount = 0; for(let depth = 0; depth < DEPTH_COUNT; depth++){ for(let row = 0; row < ROW_COUNT; row++){ const cols = []; for(let col = 0; col < COL_COUNT; col++){ const tile = tiles3x3[depth][row][col]; if(tile != null){ this.TileNumbers3x3[depth][row][col] = tile.Number; this.TilesCount++; cols.push(col); } else this.TileNumbers3x3[depth][row][col] = 0; } if(cols.length > 0){ this.LeftmostCols[depth][row] = cols[0]; this.RightmostCols[depth][row] = cols[cols.length - 1]; } } } } } |
IsSelectable関数は指定した位置の牌が選択可能かどうかを調べます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
class CheckerStalemateCourse { IsSelectable(depth, row, col){ return this.TileNumbers3x3[depth][row][col] != 0 && isTop(this.TileNumbers3x3, depth, row, col) && isEdge(this.TileNumbers3x3, depth, row, col); function isTop(tileNumbers3x3, depth, row, col){ if(depth == 0 || tileNumbers3x3[depth - 1][row][col] == 0) return true; else return false; } function isEdge(tileNumbers3x3, depth, row, col){ if(col == 0 || col == COL_COUNT - 1 || tileNumbers3x3[depth][row][col - 1] == 0 || tileNumbers3x3[depth][row][col + 1] == 0) return true; else return false; } } } |
Search関数は取り除くことができる牌のペアを配列で取得します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
class CheckerStalemateCourse { Search(){ const selectablePositions = []; for(let depth = 0; depth < DEPTH_COUNT; depth++){ for(let row = 0; row < ROW_COUNT; row++){ const left = this.LeftmostCols[depth][row]; const right = this.RightmostCols[depth][row]; if(left == right && left != -1 && this.IsSelectable(depth, row, left)){ const number = this.TileNumbers3x3[depth][row][left]; selectablePositions.push({depth:depth, row:row, col:left, number:number}); } if(left != right){ if(left != -1 && this.IsSelectable(depth, row, left)){ const number = this.TileNumbers3x3[depth][row][left]; selectablePositions.push({depth:depth, row:row, col:left, number:number}); } if(right != -1 && this.IsSelectable(depth, row, right)){ const number = this.TileNumbers3x3[depth][row][right]; selectablePositions.push({depth:depth, row:row, col:right, number:number}); } } } } const pairs = [] for(let a = 0; a < selectablePositions.length; a++){ for(let b = a + 1; b < selectablePositions.length; b++){ if(selectablePositions[a].number == selectablePositions[b].number){ const pair = [selectablePositions[a], selectablePositions[b]]; pairs.push(pair); } } } return pairs; } } |
Remove関数は指定された位置にある牌をTileNumbers3x3から取り除きます。Add関数は取り除かれた牌をもとに戻します。TileNumbers3x3だけでなくLeftmostCols、RightmostCols、TilesCountも同時に忘れず変更します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class CheckerStalemateCourse { Remove(depth, row, col, number){ if(this.TileNumbers3x3[depth][row][col] != 0){ this.TileNumbers3x3[depth][row][col] = 0; this.TilesCount--; if(this.LeftmostCols[depth][row] == col){ this.LeftmostCols[depth][row]++; if(this.LeftmostCols[depth][row] >= COL_COUNT || this.TileNumbers3x3[depth][row][this.LeftmostCols[depth][row]] == 0) this.LeftmostCols[depth][row] = -1; } if(this.RightmostCols[depth][row] == col){ this.RightmostCols[depth][row]--; if(this.RightmostCols[depth][row] < 0 || this.TileNumbers3x3[depth][row][this.RightmostCols[depth][row]] == 0) this.RightmostCols[depth][row] = -1; } } } Add(depth, row, col, number){ if(this.TileNumbers3x3[depth][row][col] == 0){ this.TileNumbers3x3[depth][row][col] = number; this.TilesCount++; if(this.LeftmostCols[depth][row] == -1) this.LeftmostCols[depth][row] = col; else if(this.LeftmostCols[depth][row] - 1 == col) this.LeftmostCols[depth][row] = col; if(this.RightmostCols[depth][row] == -1) this.RightmostCols[depth][row] = col; else if(this.RightmostCols[depth][row] + 1 == col) this.RightmostCols[depth][row] = col; } } } |
詰み確定形が発生したらこのときの牌の位置とブロッキング牌の番号を取得し、これをStalematePatterns配列に格納します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
class CheckerStalemateCourse { SaveStalematePattern(){ const depths = []; const rows = []; const cols = []; const set = new Set(); for(let depth = 0; depth < DEPTH_COUNT; depth++){ for(let row = 0; row < ROW_COUNT; row++){ for(let col = 0; col < COL_COUNT; col++){ const number = this.TileNumbers3x3[depth][row][col]; if(number > 0){ depths.push(depth); rows.push(row); cols.push(col); if(this.IsSelectable(depth, row, col)) set.add(number); } } } } this.StalematePatterns.push({depths:depths, rows:rows, cols:cols, blockingNumbers:set}); } } |
IsStalematePatterns関数はStalematePatterns配列に格納されている詰み確定形とブロッキング牌の情報から、現在の状態が詰み必至形であるかどうかを判定します。
またこれとは別に簡単にわかる詰み必至形があります。それは縦に同じ番号の牌がふたつ並んでいる場合で、もうひとつのペアはすでに取り除かれている場合です。この場合はこの牌は絶対に取り除くことができないので詰み必至形として扱います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
class CheckerStalemateCourse { IsStalematePatterns(){ const counts = []; for(let i=0; i<50; i++) counts[i] = 0; const vAlignedNumbers = []; // 縦に並んだ同じ数の牌。これが2個しかない場合、絶対に取れない for(let row = 0; row < ROW_COUNT; row++){ for(let col = 0; col < COL_COUNT; col++){ const set = new Set(); for(let depth = 0; depth < DEPTH_COUNT; depth++){ const number = this.TileNumbers3x3[depth][row][col]; if(number > 0){ counts[number]++; if(set.has(number)) vAlignedNumbers.push(number); set.add(number); } } } } for(let i=0; i<vAlignedNumbers.length; i++){ const number = vAlignedNumbers[i]; if(counts[number] == 2) return true; } for(let i=0; i<this.StalematePatterns.length; i++){ const counts2 = []; for(let i=0; i<50; i++) counts2[i] = counts[i]; const info = this.StalematePatterns[i]; let isPattern = true; for(let j=0; j<info.depths.length; j++){ const depth = info.depths[j]; const row = info.rows[j]; const col = info.cols[j]; const number = this.TileNumbers3x3[depth][row][col]; if(number == 0){ isPattern = false; // 詰みパターンではない break; } counts2[number]--; } if(isPattern){ for(let j=0; j<50; j++){ if(counts2[j] > 0){ if(info.blockingNumbers.has(j)){ isPattern = false; // 詰みパターンではない break; } } } if(isPattern) return true; } } return false; } } |
実際に判定をおこなう処理を示します。InitBeforeCheck関数で準備の処理が完了したら、結果を格納する CanGameClear と IsTimeout に false を設定します。
処理が完了したとき CanGameClear が true ならゲームクリア可能、 IsTimeout が true なら時間以内に処理が完了しなかったことを意味します。
Solve関数を再帰呼出して判定処理をおこなうのですが、前の状態を判定するさいに結果が保存されているかもしれないので、この状態から着手可能な選択をすべて試して結果を取得します。もしひとつでもゲームクリア可能な筋が存在したら詰み形ではないし、すべての初手が詰み形にしかならないのであれば現在の状態も詰み形ということになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class CheckerStalemateCourse { Check(tiles3x3){ this.InitBeforeCheck(tiles3x3); this.CanGameClear = false; this.IsTimeout = false; this.EndTime = Date.now() + 2000; if(this.CheckTopLevelOnly()) // 再帰関数を呼び出すまえに一番上の階層だけ判定処理をする return; this.Solve(); } } |
すべての初手を試す処理を示します。この関数が true を返したらすでに結果は判明しているので本処理はおこなわれません。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
class CheckerStalemateCourse { CheckTopLevelOnly(){ if(this.TilesCount == 0){ // 処理開始の段階で牌がすべて取り除かれていたら詰み形ではない this.CanGameClear = true; this.SeenTrieTree.Insert(this.LeftmostCols, this.RightmostCols, 1); return true; } let isStalemate = true; const pairs = this.Search(); for(let i=0; i<pairs.length; i++){ const pair = pairs[i]; pair.forEach(_ => this.Remove(_.depth, _.row, _.col, _.number)); const ret = this.SeenTrieTree.Matching(this.LeftmostCols, this.RightmostCols); pair.forEach(_ => this.Add(_.depth, _.row, _.col, _.number)); if(ret == 1){ // ひとつでもゲームクリアできる形にする方法があるなら詰み形ではない this.CanGameClear = true; this.SeenTrieTree.Insert(this.LeftmostCols, this.RightmostCols, 1); return true; } if(ret == 0) // ひとつでも未判定の形が存在するなら詰み形ではない isStalemate = false; } return isStalemate; } } |
あとはSolve関数を再帰呼び出しして詰み形かどうかを判定します。
牌をすべて取り除くことができたらTrie木にクリア可能という情報とともに現在の LeftmostCols と this.RightmostCols を登録します。また CanGameClear を true にして以降の再帰呼び出しが発生しないようにします。
牌を操作した結果、その状態の LeftmostCols と this.RightmostCols がTrie木に登録されているのであれば処理はおこなわずに return します。
それ以外の場合は Search関数で取り除ける牌のペアを取得して、ループを回します。ループのなかで牌を取り除き、Solve関数を再帰呼び出しします。制御が返されたら取り除いた牌をもとに戻し別の牌を取り除いた場合を試します。ただし次のループに入る前にIsStalematePatterns関数を実行してtrueが返された場合は、牌を取り除く前の状態がすでに詰み必至形になっているのでループ処理はしないで抜けるようにします。
もし終了時刻になっても処理が終了しない場合はIsTimeoutフラグでループを抜けて処理が終わるようにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
class CheckerStalemateCourse { Solve(){ if(this.TilesCount == 0){ this.CanGameClear = true; this.SeenTrieTree.Insert(this.LeftmostCols, this.RightmostCols, 1); } if(this.CanGameClear) return; if(this.IsTimeout || Date.now() > this.EndTime){ this.IsTimeout = true; return; } const ret = this.SeenTrieTree.Matching(this.LeftmostCols, this.RightmostCols); if(ret == 1 || ret == -1){ this.CanGameClear = (ret == 1); return; } const pairs = this.Search(); if(pairs.length == 0) this.SaveStalematePattern(); if(this.IsStalematePatterns()) pairs.length = 0; // すでに詰み確定なので手段なし for(let i=0; i<pairs.length; i++){ const pair = pairs[i]; pair.forEach(_ => this.Remove(_.depth, _.row, _.col, _.number)); this.Solve(); pair.forEach(_ => this.Add(_.depth, _.row, _.col, _.number)); if(this.IsStalematePatterns()) break; if(this.CanGameClear || this.IsTimeout) break; } if(!this.CanGameClear && !this.IsTimeout) this.SeenTrieTree.Insert(this.LeftmostCols, this.RightmostCols, -1); if(this.CanGameClear) this.SeenTrieTree.Insert(this.LeftmostCols, this.RightmostCols, 1); } } |
あとは新しいゲームを開始したときにCheckerStalemateCourseオブジェクトを生成し、感想戦で牌を操作したときにCheckerStalemateCourse.Check関数を呼び出すようにすれば、その操作が詰み形になっているかがリアルタイムでわかるようになります。
