点(x, y)と線分(点A(x1, y1)と点B(x2, y2)を結ぶ線分)の最短距離を求めます。いろいろなやり方があるかもしれませんが、鳩は以下のように考えました。
Contents
平行移動と回転移動で最短距離を求める
全体を平行移動させて点Aが原点にくるようにする
原点とX軸の正の部分と移動させた点Bで構成される角の角度を求める
全体をこの角度だけ逆方向に回転させる(これによって点BがX軸上にくる)
直線ABと点の距離であれば回転させた点のY座標の絶対値が距離となる
直線ABではなく線分ABとの距離であれば回転させた点のX座標によって切り分けが必要
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
public class Program { static double Solve(long x, long y, long x1, long y1, long x2, long y2) { // 並行移動させる x -= x1; y -= y1; x2 -= x1; y2 -= y1; x1 = 0; y1 = 0; // 回転させる角度を求める double angle = Math.Atan2(y2, x2); angle *= -1; // 逆方向に回転させるので double rotatedX2 = x2 * Math.Cos(angle) - y2 * Math.Sin(angle); double rotatedY2 = x2 * Math.Sin(angle) + y2 * Math.Cos(angle); // rotatedY2 は 0になっているはず double rotatedX = x * Math.Cos(angle) - y * Math.Sin(angle); double rotatedY = x * Math.Sin(angle) + y * Math.Cos(angle); if (rotatedX < 0) return Math.Sqrt(Math.Pow(rotatedX, 2) + Math.Pow(rotatedY, 2)); else if (rotatedX2 < rotatedX) return Math.Sqrt(Math.Pow(rotatedX - rotatedX2, 2) + Math.Pow(rotatedY, 2)); else return Math.Abs(rotatedY); } } |
内積を使う方法
他に線分と点の内積を使う方法があります。点Bから点AをベクトルBA、点Bから点CをベクトルBCとしたとき、ベクトルBAとベクトルBCの内積は xa × xc + ya × yc になります。またこの内積は(ベクトルBAの大きさ)×(ベクトルBCの大きさ)×cos∠ABCとなります。内積が負数になる場合は∠ABCが直角より大きくなっているので点Aから線分BCへ垂線を下ろすことができません。
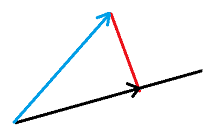
内積が正になる場合
内積が負になる場合(この場合は明らかに点から下ろした垂線は線分と交わらない)
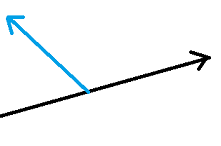
ということはベクトルBAとベクトルBCの内積が負数の場合、点Aからもっとも近いのは点Bということになります。またベクトルCAとベクトルCBの内積が負数の場合は、点Aからもっとも近いのは点Cということになります。それ以外の場合は点Aから線分BCへ垂線を下ろしたときの交点と点Aの距離が求める距離ということになります。
点Aから線分BCへ垂線を下ろした場合、直角三角形ができます。

三角比より垂線の長さは(BAの長さ)×sin∠ABCです。またベクトルBAとベクトルBCの内積は(BAの長さ)×(BCの長さ)×cos∠ABCであり、xa × xc + ya × ycです。双方を二乗するとsinとcosの2乗ができて、sin2乗 + cos2乗 = 1 なので三角関数を消すことができます。垂線の長さは(BAの長さ)と(BCの長さ)と(xa × xc + ya × yc)で表わすことができます。(BAの長さの2乗)- (内積の2乗)/(BCの長さの2乗)の平方根が求める距離となります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
static double Solve2(long x, long y, long x1, long y1, long x2, long y2) { // 並行移動させて点B(x1, y1)を原点にする x -= x1; y -= y1; x2 -= x1; y2 -= y1; x1 = 0; y1 = 0; double dot = x * x2 + y * y2; if (dot < 0) return Math.Sqrt(Math.Pow(x, 2) + Math.Pow(y, 2)); double dot2 = (x - x2) * (0 - x2) + (y - y2) * (0 - y2); if (dot2 < 0) return Math.Sqrt(Math.Pow(x - x2, 2) + Math.Pow(y - y2, 2)); double a2 = Math.Pow(x, 2) + Math.Pow(y, 2); double b2 = Math.Pow(x2, 2) + Math.Pow(y2, 2); return Math.Sqrt(a2 - Math.Pow(dot, 2) / b2); } |
