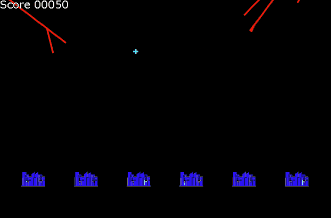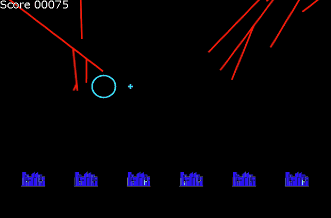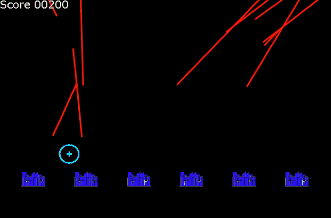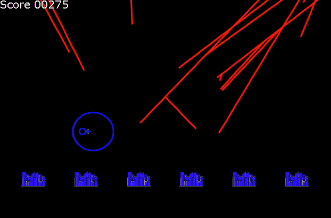
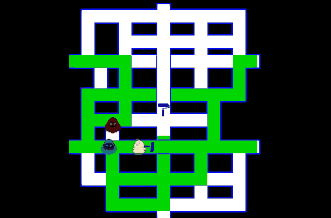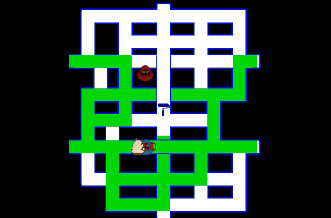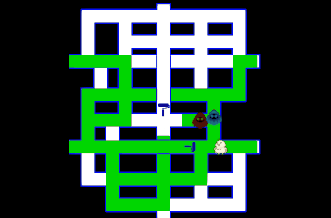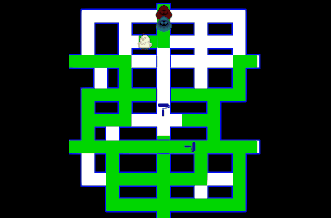
今回はボスコニアンに似たオンライン対戦ゲームをつくります。 動作確認はこちらから 『ボスコニアン』(BOSCONIAN)は、1981年11月にナムコから稼働されたアーケード用多方向スクロールシューティングゲームです。全方・・・
鳩でもわかるC#
最強のプログラミング言語はC#。その次はJavaScript。頭が悪い鳩でもわかるのだから人間様にわからないはずがナイ!
JavaScript 円形のルーレットをつくる 扇形に内接する正方形の考察
前回はJavaScriptでルーレットを作りましたが、今回は円形のルーレットをつくります。 動作確認はこちらから 扇形に内接する正方形を求める 円形のルーレットをつくる場合、扇形に内接する正方形の座標を考えなければなりま・・・
JavaScript ルーレットをつくる
JavaScriptでルーレットをつくります。 画像を連続でズラしながら描画することでルーレットが動いているように見せているだけです。簡単にできるので初心者の方にやってみてほしいと思います。 動作確認はこちらから HTM・・・
ディフェンダーに似たオンライン対戦ゲームをつくる(4)クライアントサイドの処理
ディフェンダーに似たオンライン対戦ゲームをつくる(3)の続きです。今回はクライアントサイドの処理を実装します。 動作確認はこちらから HTML部分 Pages\defender\game.cshtml [crayon-6・・・
ディフェンダーに似たオンライン対戦ゲームをつくる(3)Hubクラスの定義
ディフェンダーに似たオンライン対戦ゲームをつくる(2)の続きです。今回はクライアントとサーバー間およびサーバーからクライアント間の通信を可能にするためのHubクラスを定義します。 動作確認はこちらから [crayon-6・・・
ディフェンダーに似たオンライン対戦ゲームをつくる(2)Gameクラスの定義
ディフェンダーに似たオンライン対戦ゲームをつくる(1)の続きです。 今回はゲーム全体の処理をおこなうGameクラスを定義します。ここでやるのは各キャラクターの移動と更新、クライアントサイドで描画処理をするために必要なデー・・・
ディフェンダーに似たオンライン対戦ゲームをつくる(1)
今回はディフェンダーに似たオンライン対戦ゲームをつくります。 動作確認はこちらから 『ディフェンダー』(Defender)は1980年にウィリアムスが開発したアーケードゲームで任意横スクロールのシューティングゲームです。・・・
JavaScript じゃんけんゲームをつくる
JavaScriptでじゃんけんゲームをつくります。 動作確認はこちらから HTML部分 HTML部分を示します。 [crayon-69a54573e9f9a516972868/] style.css [crayon-6・・・
JavaScript 神経衰弱をつくる
動作確認はこちらから HTML部分 [crayon-69a54573ea17b591000678/] style.css [crayon-69a54573ea17e059788141/] JavaScript部分 グロー・・・
完成させる JavaScript ワイはあの娘とつながっているんや!をつくる(2)
JavaScript ワイはあの娘とつながっているんや!をつくる(1)の続きです。今回はゲームとして動作するようにします。 動作確認はこちらから ページが読み込まれたときの処理 ページが読み込まれたときの処理を示します。・・・