グラフ同型(グラフどうけい)とはグラフ理論における概念の一つです。
G=(V,E), G’=(V’,E’)を(単純)グラフとする。ただしVはGの頂点集合、EはGの枝の集合、同様に V’は G’の頂点集合、E’はG’の枝の集合である。Gの任意の2頂点 v,w∈Vに対して(v,w)∈Eとなるのが (f(v),f(w))∈E’となるとき、かつそのときに限るようなVから V’への全単射写像fが存在するとき、GとG’はグラフ同型(あるいは単に同型)であるといい、G’はGの同型グラフであるという。
なんかよくわからない説明ですが、このふたつのグラフは同型です。頂点番号が入れ替わっているだけです。
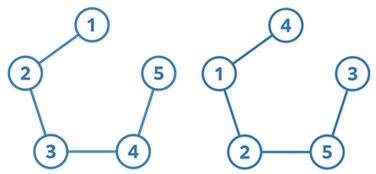
ということで問題です。
C – Make Isomorphic
頂点 1, 頂点 2, …, 頂点 N の N 個の頂点からなる単純無向グラフ G, H が与えられます。G にはMG本の辺があり、i本目の辺は頂点u_iと頂点v_iを結んでいます。H にはMH本の辺があり、i本目の辺は頂点a_iと頂点b_iを結んでいます。
あなたは、グラフ H に対して次の操作を 0 回以上の好きな回数繰り返すことができます。
1 ≦ i < j ≦ N を満たす整数の組(i, j)をひとつ選ぶ。A_[i,j]円を支払って、頂点iと頂点jを結ぶ辺がなければ追加し、あれば取り除く。
G と H を同型にするために少なくとも何円支払う必要があるか求めてください。
入力されるデータ
N
MG
u_1 v_1
u_2 v_2
:
u_MG v_MG
MH
a_1 b_1
a_2 b_2
:
a_MH b_MH
A_[1,2] A_[1,3] … A_[1,N]
A_[2,3] A_[2,4] … A_[2,N]
:
A_[N-1,N]ただし
1 ≦ N ≦ 8
1 ≦ A_[i,j] ≦ 10^6
iとjが異なるなら(u_i, v_i)≠(u_j, v_j)(a_i, b_i)≠(a_j, b_j)
解法ですが以下のとおりです。
グラフHをこれと完全に同じ形にするために必要なコストを求める
コストの最小値が答え
また順列で次のものと求めるアルゴリズムは以下となります。
arr(k) < arr(k + 1)となるようなkの最大値を探す。
(ここでkが見つからなければ次は存在しない)
STEP 2
k < l、 arr(k) < arr(l)となるlを最大値を探す。
STEP 3
arr(k) の値をarr(l)の値を入れ替える。
STEP 4
arr(k + 1)からarr(n)までを反転させる。
これが次の順列となる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
class Program { static bool NextPermutation(int[] array) { if (array.Length - 1 <= 0) return false; int end = array.Length - 1; int last = end; while (true) { int pos = last--; if (array[last].CompareTo(array[pos]) < 0) { int i; for (i = end + 1; array[last].CompareTo(array[--i]) >= 0;) { } int tmp = array[last]; array[last] = array[i]; array[i] = tmp; Array.Reverse(array, pos, end - pos + 1); return true; } if (last == 0) // 最後 { Array.Reverse(array, 0, end); return false; } } } } |
まずGとHの隣接行列 mat1 mat2 を生成します。そのあと入力されたAの値から辺の加除に必要なコストを二次元配列に格納します。
そのあと配列 array = {0, 1, …, N-1} と次の順列の取得を繰り返すことでグラフGの頂点番号を入れ替えたグラフの隣接行列 mat3 を生成します。mat2とmat3を一致させるためのコストを計算してその最小値を求めます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
using System; using System.Collections.Generic; using System.Linq; class Program { static bool NextPermutation(int[] array) // 既出 static void Main() { int N = int.Parse(Console.ReadLine()); int MG = int.Parse(Console.ReadLine()); // グラフ G の隣接行列 bool[,] mat = new bool[N, N]; for (int i = 0; i < MG; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int a = vs[0] - 1; int b = vs[1] - 1; mat[a, b] = true; mat[b, a] = true; } int MH = int.Parse(Console.ReadLine()); // グラフ H の隣接行列 bool[,] mat2 = new bool[N, N]; for (int i = 0; i < MH; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int a = vs[0] - 1; int b = vs[1] - 1; mat2[a, b] = true; mat2[b, a] = true; } // 辺の加除に必要なコスト long[,] deff = new long[N, N]; for (int i = 0; i < N - 1; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); for (int col = 0; col < vs.Length; col++) deff[i, col + i + 1] = vs[col]; } int[] array = new int[N]; for (int i = 0; i < N; i++) array[i] = i; long ans = long.MaxValue; do { // グラフGの頂点番号を入れ替えたグラフの隣接行列 bool[,] mat3 = new bool[N, N]; for (int row = 0; row < N; row++) { for (int col = 0; col < N; col++) { if (mat[row, col]) mat3[array[row], array[col]] = true; } } // コストを計算する long ret = 0; for (int row = 0; row < N; row++) { for (int col = 0; col < N; col++) { if (mat2[row, col] != mat3[row, col]) ret += deff[row, col]; } } ans = Math.Min(ans, ret); } while (NextPermutation(array)); Console.WriteLine(ans); } } |
