Contents
最小全域木とクラスカル法
最小全域木とはすべての頂点が連結されていて辺の重みの総和が最小のものです。
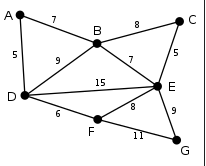
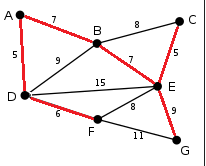
この場合は赤い部分をつなぐことで答えは39となります。
最小全域木を求める方法のひとつがKruscal(クラスカル)のアルゴリズムです。
辺集合をコストが小さい順にソートする
コストが小さい順に辺を連結させる(ただし閉路ができる場合はなにもしない)
下の動画の説明がわかりやすいです。
C# コンソールアプリで実装する
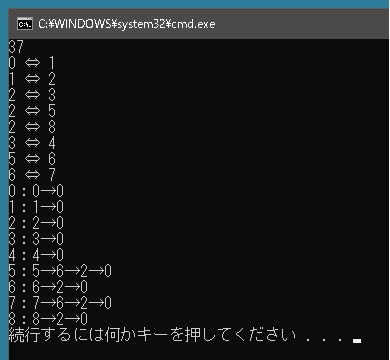
でははじめてみましょう。動画内の方法で辺の重みの総和が最小になる値を求めます。それからどの辺同士が連結されるのか、ノードの親はどうなるのかも出力させます(37と出力されるはず)。
EdgeクラスとNodeクラスの定義
Edgeクラスのコンストラクタの引数は、連結するふたつのノードの番号(最初は0)と重みです。フィールド変数のJoinは連結されているかどうかを表わすbool変数です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
public class Edge { public Edge(int nodeNum1, int nodeNum2, int weight) { NodeNum1 = nodeNum1; NodeNum2 = nodeNum2; Weight = weight; } public int NodeNum1; public int NodeNum2; public int Weight = 0; public bool Join = false; } |
Nodeクラスのコンストラクタの引数は頂点の番号です。
|
1 2 3 4 5 6 7 8 9 |
public class Node { public Node(int nodeNum) { NodeNum = nodeNum; } public int NodeNum = 0; public int Parent = -1; } |
Mainメソッド
実際の処理をおこないます。頂点の数と辺がふたつのどの頂点につながっているのか、それらの重みをリストにして、計算をするオブジェクトのメソッドに渡します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
public class Program { static void Main() { List<Node> nodes = new List<Node>(); List<Edge> edges = new List<Edge>(); int n = 9; for (int i = 0; i < n; i++) nodes.Add(new Node(i)); edges.Add(new Edge(0, 1, 4)); edges.Add(new Edge(1, 2, 8)); edges.Add(new Edge(2, 3, 7)); edges.Add(new Edge(3, 4, 9)); edges.Add(new Edge(4, 5, 10)); edges.Add(new Edge(5, 6, 2)); edges.Add(new Edge(6, 7, 1)); edges.Add(new Edge(7, 8, 7)); edges.Add(new Edge(3, 5, 14)); edges.Add(new Edge(2, 5, 4)); edges.Add(new Edge(2, 8, 2)); edges.Add(new Edge(6, 8, 6)); edges.Add(new Edge(7, 8, 7)); edges.Add(new Edge(1, 7, 11)); MyClass myClass = new MyClass(); myClass.Calculate(nodes, edges); // 解を出力する // 以下は蛇足 myClass.ShowJoinEdges(edges); myClass.ShowNodeParents(nodes); } } |
連結すると閉路ができるかどうかの判定
辺の重みを小さい順にソートしてノード同士を連結していきます。ただし閉路ができる場合は連結させません。
閉路ができるかどうかは動画にもあるとおりNodeの「親分」なるものを定義することで判断します。まだどことも連結していない頂点同士を連結するときには番号が小さいほうを親とする部分は動画と同様にしていますが、親を持つ頂点同士を連結させるときは要素数が小さなものが大きなものの直接の「子分」にするという処理はやらず、親の頂点の番号のみ比較し、番号が大きいほうが小さなものの直接の子になるようにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
public class MyClass { public void Calculate(List<Node> nodes, List<Edge> edges) { edges = edges.OrderBy(_ => _.Weight).ToList(); foreach (Edge edge in edges) { int num1 = edge.NodeNum1; int num2 = edge.NodeNum2; if (nodes[num1].Parent == -1 || nodes[num2].Parent == -1) { int parentNum = Math.Max(nodes[num1].Parent, nodes[num2].Parent); if (parentNum != -1) // 大きいほうが-1でないならそれはどこかと連結している parentNum = GetParent(parentNum, nodes); // 後述 else // 両方がどことも連結していない parentNum = Math.Min(num1, num2); nodes[num1].Parent = parentNum; // 親を設定する nodes[num2].Parent = parentNum; edge.Join = true; } else // 両方に親がいる { int parentNum1 = GetParent(num1, nodes); int parentNum2 = GetParent(num2, nodes); if (parentNum1 != parentNum2) { edge.Join = true; int numTo = Math.Min(parentNum1, parentNum2); int numFrom = Math.Max(parentNum1, parentNum2); nodes[numFrom].Parent = numTo; } } } // 連結している辺の重みの総和が求めようとしている解 Console.WriteLine(edges.Where(edge => edge.Join).Sum(_ => _.Weight)); } } |
GetParentメソッドはノードの親をたどっていき最終的な親を求めます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
public class MyClass { int GetParent(int num, List<Node> nodes) { int parent = nodes[num].Parent; while (true) { int parent2 = nodes[parent].Parent; if (parent == parent2) return parent; parent = parent2; } } } |
どの辺が連結しているのか?
蛇足部分です。どの辺が連結しているのが出力させます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
public class MyClass { public void ShowJoinEdges(List<Edge> edges) { List<string> joinEdges = new List<string>(); foreach (Edge edge in edges) { if (edge.Join) { string vertexName1 = Math.Min(edge.NodeNum1, edge.NodeNum2).ToString(); string vertexName2 = Math.Max(edge.NodeNum1, edge.NodeNum2).ToString(); joinEdges.Add($"{vertexName1} ⇔ {vertexName2}"); } } joinEdges = joinEdges.OrderBy(_ => _).ToList(); foreach (string str in joinEdges) Console.WriteLine(str); } } |
最小全域木における親はどうなっているか?
蛇足部分その2です。各頂点の親がどうなっているのか順番に出力させます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
public class MyClass { public void ShowNodeParents(List<Node> nodes) { for (int i = 0; i < nodes.Count; i++) Console.WriteLine(ShowParent(i, nodes)); } string ShowParent(int num, List<Node> nodes) { string str = $"{num}:{num}→"; int parent = nodes[num].Parent; while (true) { str += $"{parent}"; int parent2 = nodes[parent].Parent; if (parent == parent2) return str; str += "→"; parent = parent2; } } } |
上記コードを実行すると、出力は以下のようになります。動画では親は7番になっていますが、親の決め方が違っているので実行結果をみると0がすべての親になっています。