第1回岩井星人アンソロジープログラミングコンテストの問題を解いてみる（前半部分）

第1回岩井星人アンソロジープログラミングコンテストはYouTubeで競技プログラミングの実況を行っている岩井星人さんを題材にした問題のみを出題するコンテストです。ちなみに岩井星人さんはこんな方です。

「鎖国派最後の生き残り♪令和の大政翼賛会♪」なんて言っちゃってますが、真に右寄りな方ではないのでご安心ください。

ではさっそくいってみましょう。

Contents

1 No.3010 水色コーダーさん
2 No.3011 あ、俺こいつの役やりたい！
3 No.3012 岩井星人グラフ
4 No.3013 ハチマキ買い星人
5 No.3014 岩井満足性問題
- 5.1 メモリー制限に引っかかって不正解
- 5.2 正解例

No.3010 水色コーダーさん

この問題は、R_i が 1200 以上の場合、S_i の先頭4文字が “oooo” でなかった場合に気絶すると考えてよいので以下のようなコードになります。

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static void Main()
    {
        int N, M;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            M = vs[1];
        }

        int ans = 0;
        for (int i = 0; i < N; i++)
        {
            string[] vs = Console.ReadLine().Split();
            string s = vs[0];
            int r = int.Parse(vs[1]);
            if (r >= 1200 && s.Substring(0, 4) != "oooo")
                ans++;
        }
        Console.WriteLine(ans);
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

class Program

{

static void Main()

{

int N, M;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

M = vs[1];

}

int ans = 0;

for (int i = 0; i < N; i++)

{

string[] vs = Console.ReadLine().Split();

string s = vs[0];

int r = int.Parse(vs[1]);

if (r >= 1200 && s.Substring(0, 4) != "oooo")

ans++;

}

Console.WriteLine(ans);

}

No.3011 あ、俺こいつの役やりたい！

問題文はこちらです ⇒ No.3011 あ、俺こいつの役やりたい！

この問題はインタラクティブな問題（あなたの作成したプログラムとジャッジシステムが入出力を介して対話を行う形式の問題）です。

予算である N 以下の値を出力してしまった段階で即終了となり、しかも

N が報酬の 2 倍以下、別の言い方をすると最後に出力した値が N の半分以上になるようにしなければならないので最初は N が取りうる最大値（10の9乗）を出力して 0 が入力されるたびに半分の値を出力し続ければ正解となります（10の9乗が2の30乗より小さいため）。

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static void Main()
    {
        int x = (int)Math.Pow(10, 9);

        while (true)
        {
            Console.WriteLine(x);
            int r = int.Parse(Console.ReadLine());
            if (r == 0)
                x /= 2;
            else
                return;
        }
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

class Program

{

static void Main()

{

int x = (int)Math.Pow(10, 9);

while (true)

{

Console.WriteLine(x);

int r = int.Parse(Console.ReadLine());

if (r == 0)

x /= 2;

else

return;

}

No.3012 岩井星人グラフ

問題文はこちらです ⇒ No.3012 岩井星人グラフ

要はこんなグラフを出力すればよいのです（ただし頂点番号は0-indexed。回答を出力するときは1-indexedにしないといけないので注意）。

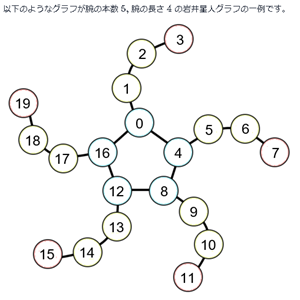
長さがYの腕を先にX本つくります。頂点を番号を0はじまりだとすれば腕の付け根の番号は Yの倍数です。以降の頂点を番号が次のYの倍数より1少ない値になるまで直線上につなげます。最後に腕の付け根を環状に連結します。

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static void Main()
    {
        int X, Y;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            X = vs[0];
            Y = vs[1];
        }

        Console.WriteLine($"{X * Y} {X * Y}");

        List<int> starts = new List<int>();
        for (int s = 0; s < X * Y; s += Y)
        {
            starts.Add(s + 1);
            for (int i = s; i < s + Y - 1; i++)
                Console.WriteLine($"{i + 1} {i + 2}");
        }

        starts.Add(1);
        for (int i = 0; i < starts.Count - 1; i++)
            Console.WriteLine($"{starts[i]} {starts[i + 1]}");
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

class Program

{

static void Main()

{

int X, Y;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

X = vs[0];

Y = vs[1];

}

Console.WriteLine($"{X * Y} {X * Y}");

List<int> starts = new List<int>();

for (int s = 0; s < X * Y; s += Y)

{

starts.Add(s + 1);

for (int i = s; i < s + Y - 1; i++)

Console.WriteLine($"{i + 1} {i + 2}");

}

starts.Add(1);

for (int i = 0; i < starts.Count - 1; i++)

Console.WriteLine($"{starts[i]} {starts[i + 1]}");

}

No.3013 ハチマキ買い星人

問題文はこちらです ⇒ No.3013 ハチマキ買い星人

移動するとカツアゲされて残金が減ります。なのであまりカツアゲされないうちに近くて買ってしまうほうがよいか、それとも多少カツアゲされても安くハチマキを買うことができる店まで移動するか、という問題です。これはカツアゲされる合計を頂点までの移動コストと考えて、店がある頂点で残金でどれだけハチマキを買えるかを考えればよいです。またハチマキはすべて同じ店で買います。複数の店で買っても同じ店で買うよりよい解を得ることはできないからです。

失敗例ダイクストラ法ではなくただの幅優先探索

ダイクストラ法ではなくただの幅優先探索で解こうとすると制限時間以内に処理は終わりません。

using System;
using System.Collections.Generic;
using System.Linq;

class Edge
{
    public Edge(int f, int n, int c)
    {
        From = f;
        Next = n;
        Cost = c;
    }
    public int From = 0;
    public int Next = 0;
    public int Cost = 0;
}

class Program
{
    static void Main()
    {
        long N, M, P, Y;
        {
            long[] vs = Console.ReadLine().Split().Select(_ => long.Parse(_)).ToArray();
            N = vs[0];
            M = vs[1];
            P = vs[2];
            Y = vs[3];
        }

        List<Edge>[] lists = new List<Edge>[N];
        for (int i = 0; i < N; i++)
            lists[i] = new List<Edge>();

        for (int i = 0; i < M; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int a = vs[0] - 1;
            int b = vs[1] - 1;
            int c = vs[2];
            lists[a].Add(new Edge(a, b, c));
            lists[b].Add(new Edge(b, a, c));
        }

        // 幅優先探索で各頂点までの移動コストを求めようとしている
        long[] costs = new long[N];
        for (int i = 0; i < N; i++)
            costs[i] = long.MaxValue;

        costs[0] = 0;
        Queue<int> q = new Queue<int>();
        q.Enqueue(0);
        while (q.Count > 0)
        {
            int cur = q.Dequeue();
            long cost = costs[cur];
            foreach (Edge edge in lists[cur])
            {
                long ncost = cost + edge.Cost;
                int next = edge.Next;
                if (costs[next] > ncost)
                {
                    costs[next] = ncost;
                    q.Enqueue(next);
                }
            }
        }

        // その頂点に店があるなら残金でハチマキを買えるだけ買ったときの本数を計算する
        long ans = 0;
        for (int i = 0; i < P; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int a = vs[0] - 1;
            int c = vs[1];
            if (Y - costs[a] > 0)
                ans = Math.Max(ans, (Y - costs[a]) / c);
        }
        Console.WriteLine(ans);
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

class Edge

{

public Edge(int f, int n, int c)

{

From = f;

Next = n;

Cost = c;

}

public int From = 0;

public int Next = 0;

public int Cost = 0;

}

class Program

{

static void Main()

{

long N, M, P, Y;

{

long[] vs = Console.ReadLine().Split().Select(_ => long.Parse(_)).ToArray();

N = vs[0];

M = vs[1];

P = vs[2];

Y = vs[3];

}

List<Edge>[] lists = new List<Edge>[N];

for (int i = 0; i < N; i++)

lists[i] = new List<Edge>();

for (int i = 0; i < M; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int a = vs[0] - 1;

int b = vs[1] - 1;

int c = vs[2];

lists[a].Add(new Edge(a, b, c));

lists[b].Add(new Edge(b, a, c));

}

// 幅優先探索で各頂点までの移動コストを求めようとしている

long[] costs = new long[N];

for (int i = 0; i < N; i++)

costs[i] = long.MaxValue;

costs[0] = 0;

Queue<int> q = new Queue<int>();

q.Enqueue(0);

while (q.Count > 0)

{

int cur = q.Dequeue();

long cost = costs[cur];

foreach (Edge edge in lists[cur])

{

long ncost = cost + edge.Cost;

int next = edge.Next;

if (costs[next] > ncost)

{

costs[next] = ncost;

q.Enqueue(next);

}

// その頂点に店があるなら残金でハチマキを買えるだけ買ったときの本数を計算する

long ans = 0;

for (int i = 0; i < P; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int a = vs[0] - 1;

int c = vs[1];

if (Y - costs[a] > 0)

ans = Math.Max(ans, (Y - costs[a]) / c);

}

Console.WriteLine(ans);

}

普通の幅優先探索と異なりダイクストラ法は

始点から移動可能な頂点への移動コストの暫定値を計算・記憶しておき、そのなかから最小のものを取り出します。辺の重みがすべて非負数であればその値が更新されることはないので確定させる。移動コストが確定した頂点から移動可能な頂点から移動できる頂点への移動コストの暫定値を計算する……という処理を繰り返す

という方法です。こうすることで無駄な探索と値の更新をなくしています。そしてキューのなかから移動コストが最小のものを取り出すためには優先度付きキュー（PriorityQueue）を使わなければなりません。

失敗例正しくないダイクストラ法

ただし上記コードのQueueをPriorityQueueに取り替えただけでは不十分です。TLE（時間切れ）の件数は減りましたが、やはりすべてのテストケースを通すことができません。

class Program
{
    static void Main()
    {
        // 省略

        List<Edge>[] lists = new List<Edge>[N];
        for (int i = 0; i < N; i++)
            lists[i] = new List<Edge>();

        for (int i = 0; i < M; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int a = vs[0] - 1;
            int b = vs[1] - 1;
            int c = vs[2];
            lists[a].Add(new Edge(a, b, c));
            lists[b].Add(new Edge(b, a, c));
        }
        long[] costs = new long[N];
        for (int i = 0; i < N; i++)
            costs[i] = long.MaxValue;

        costs[0] = 0;
        PriorityQueue<int, long> pq = new PriorityQueue<int, long>();
        pq.Enqueue(0, 0);
        while (pq.Count > 0)
        {
            int cur = pq.Dequeue();
            long cost = costs[cur];
            foreach (Edge edge in lists[cur])
            {
                long ncost = cost + edge.Cost;
                int next = edge.Next;
                if (costs[next] > ncost)
                {
                    costs[next] = ncost;
                    pq.Enqueue(next, ncost);
                }
            }
        }

        // 省略
    }
}

class Program

{

static void Main()

{

// 省略

List<Edge>[] lists = new List<Edge>[N];

for (int i = 0; i < N; i++)

lists[i] = new List<Edge>();

for (int i = 0; i < M; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int a = vs[0] - 1;

int b = vs[1] - 1;

int c = vs[2];

lists[a].Add(new Edge(a, b, c));

lists[b].Add(new Edge(b, a, c));

}

long[] costs = new long[N];

for (int i = 0; i < N; i++)

costs[i] = long.MaxValue;

costs[0] = 0;

PriorityQueue<int, long> pq = new PriorityQueue<int, long>();

pq.Enqueue(0, 0);

while (pq.Count > 0)

{

int cur = pq.Dequeue();

long cost = costs[cur];

foreach (Edge edge in lists[cur])

{

long ncost = cost + edge.Cost;

int next = edge.Next;

if (costs[next] > ncost)

{

costs[next] = ncost;

pq.Enqueue(next, ncost);

}

// 省略

}

正解例正しいダイクストラ法

ダイクストラ法では、始点から移動可能な頂点への移動コストの暫定値を計算・記憶しておき、そのなかから最小のものを取り出し、この値を確定させます。確定したあとであってもPriorityQueueから同じ頂点への移動コストに関する情報は取り出され続けるので、確定後はそれらは無視しなければなりまん。そうでないと無駄な処理が発生して制限時間以内に終わりません。

using System;
using System.Collections.Generic;
using System.Linq;

class Edge
{
    public Edge(int f, int n, int c)
    {
        From = f;
        Next = n;
        Cost = c;
    }
    public int From = 0;
    public int Next = 0;
    public int Cost = 0;
}

class Program
{
    static void Main()
    {
        long N, M, P, Y;
        {
            long[] vs = Console.ReadLine().Split().Select(_ => long.Parse(_)).ToArray();
            N = vs[0];
            M = vs[1];
            P = vs[2];
            Y = vs[3];
        }

        List<Edge>[] lists = new List<Edge>[N];
        for (int i = 0; i < N; i++)
            lists[i] = new List<Edge>();

        for (int i = 0; i < M; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int a = vs[0] - 1;
            int b = vs[1] - 1;
            int c = vs[2];
            lists[a].Add(new Edge(a, b, c));
            lists[b].Add(new Edge(b, a, c));
        }

        long[] costs = new long[N];
        for (int i = 0; i < N; i++)
            costs[i] = long.MaxValue;

        bool[] seen = new bool[N]; // 確定済みかチェックする

        costs[0] = 0;
        PriorityQueue<int, long> pq = new PriorityQueue<int, long>();
        pq.Enqueue(0, 0);
        while (pq.Count > 0)
        {
            int cur = pq.Dequeue();

            if(seen[cur]) // すでに移動コストが確定した頂点であれば無視
                continue;

            seen[cur] = true;

            long cost = costs[cur];
            foreach (Edge edge in lists[cur])
            {
                long ncost = cost + edge.Cost;
                int next = edge.Next;
                if (costs[next] > ncost)
                {
                    costs[next] = ncost;
                    pq.Enqueue(next, ncost);
                }
            }
        }
        long ans = 0;
        for (int i = 0; i < P; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            int a = vs[0] - 1;
            int c = vs[1];
            if (Y - costs[a] > 0)
                ans = Math.Max(ans, (Y - costs[a]) / c);
        }
        Console.WriteLine(ans);
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

class Edge

{

public Edge(int f, int n, int c)

{

From = f;

Next = n;

Cost = c;

}

public int From = 0;

public int Next = 0;

public int Cost = 0;

}

class Program

{

static void Main()

{

long N, M, P, Y;

{

long[] vs = Console.ReadLine().Split().Select(_ => long.Parse(_)).ToArray();

N = vs[0];

M = vs[1];

P = vs[2];

Y = vs[3];

}

List<Edge>[] lists = new List<Edge>[N];

for (int i = 0; i < N; i++)

lists[i] = new List<Edge>();

for (int i = 0; i < M; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int a = vs[0] - 1;

int b = vs[1] - 1;

int c = vs[2];

lists[a].Add(new Edge(a, b, c));

lists[b].Add(new Edge(b, a, c));

}

long[] costs = new long[N];

for (int i = 0; i < N; i++)

costs[i] = long.MaxValue;

bool[] seen = new bool[N]; // 確定済みかチェックする

costs[0] = 0;

PriorityQueue<int, long> pq = new PriorityQueue<int, long>();

pq.Enqueue(0, 0);

while (pq.Count > 0)

{

int cur = pq.Dequeue();

if(seen[cur]) // すでに移動コストが確定した頂点であれば無視

continue;

seen[cur] = true;

long cost = costs[cur];

foreach (Edge edge in lists[cur])

{

long ncost = cost + edge.Cost;

int next = edge.Next;

if (costs[next] > ncost)

{

costs[next] = ncost;

pq.Enqueue(next, ncost);

}

long ans = 0;

for (int i = 0; i < P; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int a = vs[0] - 1;

int c = vs[1];

if (Y - costs[a] > 0)

ans = Math.Max(ans, (Y - costs[a]) / c);

}

Console.WriteLine(ans);

}

No.3014 岩井満足性問題

問題文はこちらです ⇒ No.3014 岩井満足性問題

動的計画法の問題ですが、単純なナップサック問題とちがって満足度と美しさというふたつの要素があります。そこで最初は2次元配列ではなく3次元配列を用いた方法を考えてみることにします。

メモリー制限に引っかかって不正解

以下のコードはやり方はあっているはずなのですが、メモリー制限に引っかかって不正解です。

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static void Main()
    {
        int N, D, K;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            D = vs[1];
            K = vs[2];
        }

        int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
        int[] C = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

        // 3次元配列を定義してlong.MinValueで初期化する
        long[,,] dp = new long[N + 1, D + 1, K + 1];
        for (int a = 0; a < dp.GetLength(0); a++)
        {
            for (int b = 0; b < dp.GetLength(1); b++)
            {
                for (int c = 0; c < dp.GetLength(2); c++)
                    dp[a, b, c] = long.MinValue;
            }
        }

        // 最初はなにも選択していないので0個までを選択するかどうかを決定し、実際に0個が選択され、
        // その美しさは0という状態のみが存在する。それ以外の場合は存在しない
        dp[0, 0, 0] = 0;

        for (int i = 0; i < A.Length; i++)
        {
            for (int b = 0; b < dp.GetLength(1); b++)
            {
                for (int c = 0; c < dp.GetLength(2); c++)
                {
                    // 存在しない場合はなにもしない
                    if (dp[i, b, c] == long.MinValue)
                        continue;

                    // i 番目の問題は選択しない場合
                    dp[i + 1, b, c] = Math.Max(dp[i, b, c], dp[i + 1, b, c]);

                    // すでに D 個選択しているのであれば continue
                    if(b >= D)
                        continue;

                    // i 番目の問題は選択した結果、美しさが Kを超える場合は
                    // dp[i + 1, b + 1, K]に値を格納する
                    if (c + C[i] < K)
                        dp[i + 1, b + 1, c + C[i]] = Math.Max(dp[i, b, c] + A[i], dp[i + 1, b + 1, c + C[i]]);
                    else
                        dp[i + 1, b + 1, K] = Math.Max(dp[i, b, c] + A[i], dp[i + 1, b + 1, K]);
                }
            }
        }

        // dp[N, D, K] に long.MinValue 以外の値が格納されていたらそれが満足度の最大値
        if(dp[N, D, K] > long.MinValue)
            Console.WriteLine(dp[N, D, K]);
        else
            Console.WriteLine("No");
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

class Program

{

static void Main()

{

int N, D, K;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

D = vs[1];

K = vs[2];

}

int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int[] C = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

// 3次元配列を定義してlong.MinValueで初期化する

long[,,] dp = new long[N + 1, D + 1, K + 1];

for (int a = 0; a < dp.GetLength(0); a++)

{

for (int b = 0; b < dp.GetLength(1); b++)

{

for (int c = 0; c < dp.GetLength(2); c++)

dp[a, b, c] = long.MinValue;

}

// 最初はなにも選択していないので0個までを選択するかどうかを決定し、実際に0個が選択され、

// その美しさは0という状態のみが存在する。それ以外の場合は存在しない

dp[0, 0, 0] = 0;

for (int i = 0; i < A.Length; i++)

{

for (int b = 0; b < dp.GetLength(1); b++)

{

for (int c = 0; c < dp.GetLength(2); c++)

{

// 存在しない場合はなにもしない

if (dp[i, b, c] == long.MinValue)

continue;

// i 番目の問題は選択しない場合

dp[i + 1, b, c] = Math.Max(dp[i, b, c], dp[i + 1, b, c]);

// すでに D 個選択しているのであれば continue

if(b >= D)

continue;

// i 番目の問題は選択した結果、美しさが Kを超える場合は

// dp[i + 1, b + 1, K]に値を格納する

if (c + C[i] < K)

dp[i + 1, b + 1, c + C[i]] = Math.Max(dp[i, b, c] + A[i], dp[i + 1, b + 1, c + C[i]]);

else

dp[i + 1, b + 1, K] = Math.Max(dp[i, b, c] + A[i], dp[i + 1, b + 1, K]);

}

// dp[N, D, K] に long.MinValue 以外の値が格納されていたらそれが満足度の最大値

if(dp[N, D, K] > long.MinValue)

Console.WriteLine(dp[N, D, K]);

else

Console.WriteLine("No");

}

正解例

3次元配列の各行は次の行の値が確定したら使わないので2次元配列で済むように書き換えます。

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static void Main()
    {
        int N, D, K;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            D = vs[1];
            K = vs[2];
        }

        int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
        int[] C = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

        long[,] dp = new long[D + 1, K + 1];
        for (int d = 0; d <= D; d++)
        {
            for (int k = 0; k <= K; k++)
                dp[d, k] = long.MinValue;
        }

        dp[0, 0] = 0;

        for (int i = 0; i < A.Length; i++)
        {
            long[,] nextdp = new long[D + 1, K + 1];
            for (int d = 0; d <= D; d++)
            {
                for (int k = 0; k <= K; k++)
                    nextdp[d, k] = long.MinValue;
            }

            for (int d = 0; d <= D; d++)
            {
                for (int k = 0; k <= K; k++)
                {
                    if (dp[d, k] == long.MinValue)
                        continue;

                    nextdp[d, k] = Math.Max(dp[d, k], nextdp[d, k]);
                    if(d >= D)
                        continue;

                    if (k + C[i] < K)
                        nextdp[d + 1, k + C[i]] = Math.Max(dp[d, k] + A[i], nextdp[d + 1, k + C[i]]);
                    else
                        nextdp[d + 1, K] = Math.Max(dp[d, k] + A[i], nextdp[d + 1, K]);
                }
            }
            dp = nextdp;
        }
        if(dp[D, K] > long.MinValue)
            Console.WriteLine(dp[D, K]);
        else
            Console.WriteLine("No");
    }
}

using System;

using System.Collections.Generic;

using System.Linq;

class Program

{

static void Main()

{

int N, D, K;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

D = vs[1];

K = vs[2];

}

int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

int[] C = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

long[,] dp = new long[D + 1, K + 1];

for (int d = 0; d <= D; d++)

{

for (int k = 0; k <= K; k++)

dp[d, k] = long.MinValue;

}

dp[0, 0] = 0;

for (int i = 0; i < A.Length; i++)

{

long[,] nextdp = new long[D + 1, K + 1];

for (int d = 0; d <= D; d++)

{

for (int k = 0; k <= K; k++)

nextdp[d, k] = long.MinValue;

}

for (int d = 0; d <= D; d++)

{

for (int k = 0; k <= K; k++)

{

if (dp[d, k] == long.MinValue)

continue;

nextdp[d, k] = Math.Max(dp[d, k], nextdp[d, k]);

if(d >= D)

continue;

if (k + C[i] < K)

nextdp[d + 1, k + C[i]] = Math.Max(dp[d, k] + A[i], nextdp[d + 1, k + C[i]]);

else

nextdp[d + 1, K] = Math.Max(dp[d, k] + A[i], nextdp[d + 1, K]);

}

dp = nextdp;

}

if(dp[D, K] > long.MinValue)

Console.WriteLine(dp[D, K]);

else

Console.WriteLine("No");

}

第1回岩井星人アンソロジープログラミングコンテストの問題を解いてみる（前半部分）

No.3010 水色コーダーさん

No.3011 あ、俺こいつの役やりたい！

No.3012 岩井星人グラフ

No.3013 ハチマキ買い星人

失敗例ダイクストラ法ではなくただの幅優先探索

失敗例正しくないダイクストラ法

正解例正しいダイクストラ法

No.3014 岩井満足性問題

メモリー制限に引っかかって不正解

正解例

鳩でも分かるC#管理人からのお願い

コメントについて

管理人のモチベーションアップのために

コメントをどうぞ

No.3010 水色コーダーさん

No.3011 あ、俺こいつの役やりたい！

No.3012 岩井星人グラフ

No.3013 ハチマキ買い星人

失敗例 ダイクストラ法ではなくただの幅優先探索

失敗例 正しくないダイクストラ法

正解例 正しいダイクストラ法

No.3014 岩井満足性問題

メモリー制限に引っかかって不正解

正解例

鳩でも分かるC#管理人からのお願い

コメントについて

管理人のモチベーションアップのために

コメントをどうぞ

失敗例ダイクストラ法ではなくただの幅優先探索

失敗例正しくないダイクストラ法

正解例正しいダイクストラ法