最大流問題とはネットワーク上で始点から終点まで流すことができる量の最大値を求める問題です
たとえば各地点が水道管でつながっていて、それぞれの水道管にはそれぞれ別の流すことができる水の量が定まっていると考えます。この場合、始点と終点以外では各地点に流れ込む水の量と出ていく水の量は同じです。水は各地点で分岐したり合流しながら終点まで到着します。この水の流れをフローと呼びます。
ここでは頂点が6つ、頂点同士をつなぐ辺が9つあります。では頂点sからtまで流すことができる水の量はどうなるでしょうか?
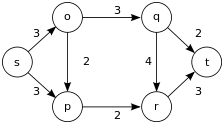
始点から終点まで流すことができるパスを求め、フローの流量を求め、通過した辺の容量をそのぶん減らす、また始点から終点まで流すことができる別のパスを求めフローを流すのを繰り返すという方法でよさそうですが、それだとうまくいかない場合があります。
そこで鍵となるのが逆辺です。ある辺にフローを流すと、その辺の容量は流した分だけ減り、逆向きの辺の容量が流した分だけ増えるという考え方です。これを繰り返すことで最大流を求めることができるようになります。
下の動画の説明はわかりやすいです。
ただこの動画ではなぜ逆辺が必要なのかがちょっとわかりにくいです。そこで要領が悪いパスの選び方をあえてしてみることにします。
こんな問題が出されたとします。これなら考えるまでもなく、答えは35です。0→1→3を20、0→2→3を15、あわせて35です。
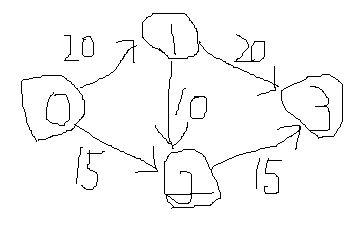
ところが0→1→2→3というパスを最初に選択して10のフローを流してしまうと(下図)、0→1→3には10のフローを流したあと0→2→3には5のフローしか流せず合計は正しい値になりません。
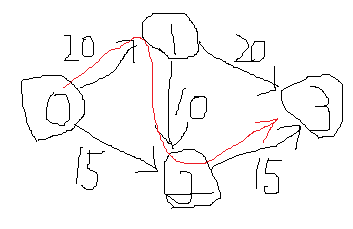
しかし逆辺があれば要領が悪いパスを選んだとしても(下図)、0→1→3に10のフローを流して、0→2→3に5のフローを流し、0→2→1→3に10のフローを流すことができるので合計は35となり正しい値を得ることができます。
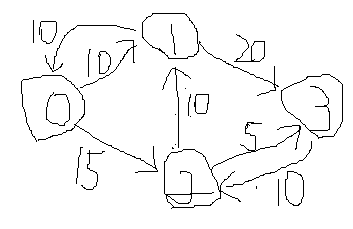
ではC#でプログラミングしてみましょう。
MyClassクラスを定義していますが、とくに意味はありません。Mainメソッド内でフィールド変数を参照したり別のメソッドを呼び出そうとするとstaticをつけなければならないのが面倒だからという理由です。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main(string[] args) { MyClass myClass = new MyClass(); myClass.Calculate(); } } |
Edgeクラスを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
public class Edge { public Edge(int from, int to, int capacity) { From = from; To = to; Capacity = capacity; } public int From = 0; public int To = 0; public int Capacity = 0; } |
標準入力から以下のような入力がされます。
|
1 2 3 4 5 |
n, m, s, t a_0 b_0 c_0 a_1 b_1 c_1 ... a_(m-1) b_(m-1) c_(m-1) |
1行目は頂点数を表す整数 n, グラフの辺数を表す整数 m, フローの始点、終点の頂点の番号です。続く m 行では、各辺の情報(辺の始点、終点の頂点の番号、流せる最大の流量)が与えられます。
たとえば

であるなら標準入力からは以下のような入力がされます。
|
1 2 3 4 5 6 7 8 9 |
6 8 0 5 0 1 3 1 2 3 2 5 2 0 3 3 3 4 2 4 5 3 1 3 2 2 4 4 |
標準入力から出力を求める処理は以下のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
public class MyClass { public void Calculate() { int n, m, s, t; { int[] ints = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); n = ints[0]; m = ints[1]; s = ints[2]; t = ints[3]; } List<List<Edge>> edgesList = new List<List<Edge>>(); for (int i = 0; i < n; i++) edgesList.Add(new List<Edge>()); for (int i = 0; i < m; i++) { int[] ints = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int from = ints[0]; int to = ints[1]; int capacity = ints[2]; edgesList[from].Add(new Edge(from, to, capacity)); edgesList[to].Add(new Edge(to, from, 0)); } int ret = 0; while (true) { List<Edge> path = new List<Edge>(); if(!SearchPath(n, s, t, edgesList, path)) break; int min = path.Min(_ => _.Capacity); foreach (Edge edge in path) { edge.Capacity -= min; Edge edge2 = edgesList[edge.To].FirstOrDefault(_ => _.From == edge.To && _.To == edge.From); if (edge2 != null) edge2.Capacity += min; } ret += min; } Console.WriteLine(ret); } } |
これは始点から終点まで流すことができるパスが存在するか、存在する場合はどれかを取得するメソッドです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
public class MyClass { bool SearchPath(int n, int s, int t, List<List<Edge>> edgesList, List<Edge> path) { bool[] isVisits = new bool[n]; Edge[] fromEdge = new Edge[n]; Queue<int> queue = new Queue<int>(); queue.Enqueue(s); while (queue.Count > 0) { int num = queue.Dequeue(); isVisits[num] = true; if (num == t) { List<Edge> edges = new List<Edge>(); int i = t; while (true) { Edge edge = fromEdge[i]; edges.Add(edge); i = edge.From; if (edge.From == s) break; } foreach (Edge edge1 in edges) path.Add(edge1); return true; } foreach (Edge edge in edgesList[num]) { if (edge.Capacity <= 0) continue; if (isVisits[edge.To]) continue; queue.Enqueue(edge.To); fromEdge[edge.To] = edge; } } return false; } } |
