イベントソートとはクエリをそれに関連する時刻や位置の順にソートして順番に処理する方法です。この方法を採用することで計算量を落とすことができる場合があります。
Contents
E – Roadwork
東西に無限に続く 1 本の大通りがあり、数直線とみなすことができます。
この大通り上で N 回道路工事が行われます。 i 番目の道路工事は時刻 S_i – 0.5 から時刻 T_i – 0.5 まで座標 X_i を通行止めにします。
Q 人の人が座標 0 に立っています。 i 番目の人は時刻 D_i に座標 0 を出発し、速度 1 で正の方向へ歩き続けます。歩いている途中で通行止めとなっている地点に到達した場合には、そこで歩くのをやめます。
Q 人それぞれが進む距離を求めてください。
入力されるデータ
N Q
S_1 T_1 X_1
S_2 T_2 X_2
:
S_N T_N X_N
D_1
D_2
:
D_Qただし、
1 ≦ N, Q ≦ 2 × 10^5
0 ≦ S_i < T_i ≦ 10^9
1 ≦ X_i ≦ 10^9
0 ≦ D_1 < D_2 < … < D_Q ≦ 10^9
方針
i 番目の道路工事は時刻 S_i – 0.5 から時刻 T_i – 0.5の間、座標 X_i を通行止めにします。逆算して考えると、この通行止めの影響を受ける可能性があるのは 時刻 S_i – 0.5 – X_i から時刻 T_i – 0.5 – X_i の間に座標 0 を出発した人だけです。そのため i 番目の人が進める距離は、その人が影響を受ける可能性がある道路工事のなかで、それらの座標が最も小さいものです。
しかし、Q 人それぞれについて、N 個の道路工事がその人に影響するかどうかを調べてしまうと、時間計算量がO(NQ) となり、N, Q の最大値が 2 × 10^5 であるという条件下では制限時間(2秒)以内に処理を完了することができません。
そこでイベントソートを使います。イベントを格納する配列と現時点で通行止めにされている座標を持つセットを 1 つずつ用意し、時刻 t における 2 種類のイベントを定義します。
追加イベント (t, 1, x) – セットに x を追加する。
削除イベント (t, -1, x) – セットから x を削除する。
そして、N 個の道路工事全てについて、i 番目の道路工事が開始されたら S_i – X_i – 0.5 に座標 0 を出発した人が通行止めの影響を受けるので t = S_i – X_i – 0.5, 1, x = X_i で追加イベントを追加し、道路工事が終了したらその工事による通行止めの影響はなくなるので t = T_i – X_i – 0.5, x = X_i で削除イベントを追加します。
配列に追加したイベントは t の値でソートし、順番に処理します。
i 番目の人に対する答えを格納する配列を定義し、-1 で初期化しておきます。i 番目の人に対する答えを求めるときは t の値が Di より小さいイベントをすべて処理し終わったタイミングで、セットの最小値を調べればどの座標で通行止めの影響をうけて停止するかがわかります。
こうしてイベントのソートの計算量は O(N log N)、各イベントの計算量は O(log N)、各 Q 人が停止する座標を求める計算量は O(log N) なので、全体の計算量は O((N + Q) log N) となります。
実装してみる
まずEventクラスを定義します。イベントのIDには追加と削除で対になるものには同じIDをつけます。Type は追加が 1、削除なら -1 です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
class Event { public Event(int id, double time, int type, int x) { ID = id; Time = time; Type = type; X = x; } public int ID = 0; // イベントのIDには追加と削除で対になるものには同じIDをつける public double Time = 0; public int Type = 0; public int X = 0; } |
入力を受け取ってイベントオブジェクトを生成してリストに格納します。そしてソートします。そのあと Q 人の人が座標 0 を出発する時刻 D_i を取得し、配列に格納します。そのあと Solve メソッドで求解します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
class Program { static List<Event> events = new List<Event>(); static int N, Q; static int[] D = { }; static void Main() { int[] nq = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = nq[0]; Q = nq[1]; for (int i = 0; i < N; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); events.Add(new Event(vs[0] - vs[2] - 0.5, 1, vs[2])); events.Add(new Event(vs[1] - vs[2] - 0.5, -1, vs[2])); } events = events.OrderBy(_ => _.Time).ToList(); D = new int[Q]; for (int i = 0; i < Q; i++) D[i] = int.Parse(Console.ReadLine()); Solve(); } } |
C++ には multiset があるのだが・・・
C++ には multiset があり、要素の追加・削除、最大値・最小値の取得が高速にできます。C#の場合はどうでしょうか?
残念ながら以下のコードでは1件だけ制限時間以内に処理を完了することができず、不正解となります。おそらく list.Remove(events[k].X) や list.Min() で時間がかかっているのではないかと思われます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
class Program { static void Solve() { List<int> list = new List<int>(); int k = 0; for (int i = 0; i < Q; i++) { // D[i]以下のイベントを全て処理する while (events.Count > k && events[k].Time < D[i]) { if (events[k].Type == 1) list.Add(events[k].X); if (events[k].Type == -1) list.Remove(events[k].X); k++; } if (list.Count > 0) { int min = list.Min(); Console.WriteLine(min); } else { Console.WriteLine(-1); } } } } |
優先度つきキューで解決?
優先度つきキューであれば先頭の要素の取得や削除が計算量 O(1) や O(log n) でおこなうことができます。優先度つきキューに値を追加し、削除するときはそれが無効であるというマークをつけます。そして最小値を求めるときは、先頭から値を調べてマークがついていないものを探します。
Pairクラスは値が有効かどうかを管理するためのものです。
|
1 2 3 4 5 6 7 8 9 |
class Pair { public Pair(int value) { Value = value; } public int Value = 0; public bool IsDead = false; } |
辞書で優先度つきキューのどこかに格納されているPairオブジェクトにダイレクトにアクセスできるようにします。辞書に追加するときのキーはイベントのIDを使います。削除するときは辞書からオブジェクトへの参照を取得して IsDead を true にします。最小値を取得するときは優先度つきキューの先頭から IsDead が true のものを取り除き、最初に見つけた IsDead が false のオブジェクトの Value を最小値としています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class Program { static void Solve() { Dictionary<int, Pair> dic = new Dictionary<int, Pair>(); PriorityQueue<Pair, int> pq = new PriorityQueue<Pair, int>(); int k = 0; for (int i = 0; i < Q; i++) { while (events.Count > k && events[k].Time < D[i]) { if (events[k].Type == 1) { Pair pair = new Pair(events[k].X); pq.Enqueue(pair, events[k].X); dic.Add(events[k].ID, pair); } if (events[k].Type == -1) { Pair pair = dic[events[k].ID]; pair.IsDead = true; } k++; } while (pq.Count > 0 && pq.Peek().IsDead) pq.Dequeue(); if (pq.Count > 0) Console.WriteLine(pq.Peek().Value); else Console.WriteLine(-1); } } } |
F – Range Connect MST
N + Q 頂点のグラフがあり、頂点には 1, 2, …, N + Q の番号がついています。グラフにははじめ辺がありません。
このグラフに対して i = 1, 2, …, Q の順に以下の操作を行います。
L_i ≦ j ≦ R_i を満たす各整数 j について頂点 N + i と頂点 j の間にコスト C_i の無向辺を追加する
すべての操作を終えた後グラフは連結であるか判定し、連結である場合はこのグラフの最小全域木のコストを求めてください。ただし最小全域木とはコストが最小の全域木のことを指し、全域木のコストとは全域木に使われた辺のコストの和のことを指します。
入力されるデータ
N Q
L_1 R_1 C_1
L_2 R_2 C_2
:
L_Q R_Q C_Q
(ただし 1 ≦ N, Q ≦ 2×10^5
1 ≦ L_i ≦ R i ≦ N
1 ≦ C_i ≦ 10^9 )
最小全域木のコストはクラスカルのアルゴリズムで求めることができます。辺のコストを小さい順にソートし、閉路ができないように追加していく方法です。しかしこの問題の場合、N, Q が大きくL_i と R_i の差が大きい場合、グラフに追加される辺の数が大きくなる可能性があり、計算量を落とす工夫が必要です。
この問題は 1 ~ N の頂点から N + 1 ~ Q の頂点のふたつのグループにわかれています。そして以下の図のように辺を張り替えても最小全域木のコストは変わらないことがわかります。
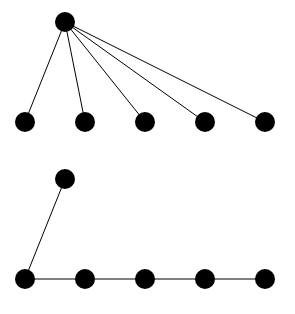
そして複数の辺が重複している部分はもっともコストが小さい辺を採用すれば最小全域木をつくることができることがわかります。
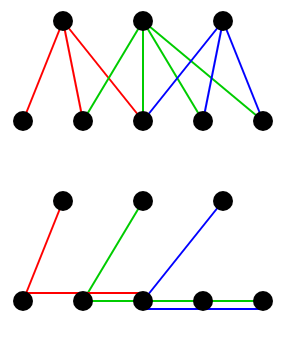
ということで、この問題もイベントソートで解くことができます。i が L_i なら C_i の追加イベント、R_i なら削除イベントを定義します。次に cur を 0 から N – 2 の間で動かし、ループのなかで i が cur 以下のイベントをすべて処理したあと優先度つきキューのなかの最小値を求めます。
これらの総和とC_iの総和の合計が求める解となります。途中で優先度つきキューが空になった場合はグラフは連結していないということなので -1 を出力します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |
using System; using System.Collections.Generic; using System.Linq; class Event { public Event(int id, int index, int type, int cost) { ID = id; Index = index; Type = type; Cost = cost; } public int ID = 0; public int Index = 0; public int Type = 0; public int Cost = 0; } class Pair { public Pair(int value) { Value = value; } public int Value = 0; public bool IsDead = false; } class Program { static void Main() { int N, Q; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; Q = vs[1]; } List<Event> events = new List<Event>(); long ans = 0; for (int q = 0; q < Q; q++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int left = vs[0] - 1; int right = vs[1] - 1; int cost = vs[2]; events.Add(new Event(q, left, 1, cost)); events.Add(new Event(q, right, -1, cost)); ans += cost; } events = events.OrderBy(_ => _.Index).ToList(); Dictionary<int, Pair> dic = new Dictionary<int, Pair>(); PriorityQueue<Pair, int> pq = new PriorityQueue<Pair, int>(); int i = 0; for (int cur = 0; cur < N - 1; cur++) { while (events.Count > i && events[i].Index <= cur) { if (events[i].Type == 1) { Pair pair = new Pair(events[i].Cost); pq.Enqueue(pair, events[i].Cost); dic.Add(events[i].ID, pair); } if (events[i].Type == -1) { Pair pair = dic[events[i].ID]; pair.IsDead = true; } i++; } while (pq.Count > 0 && pq.Peek().IsDead) pq.Dequeue(); if (pq.Count > 0) ans += pq.Peek().Value; else { // 優先度つきキューが途中で空になった場合はグラフは連結していないので -1 を出力 Console.WriteLine(-1); return; } } Console.WriteLine(ans); } } |
