C#でエイト・クイーン問題を解いてみましょう。

チェスの駒・クイーンは、上下左右斜めの8方向に遮る物がない限り進むことができます。将棋の飛車と角行を合わせた動きです。さてチェスの盤上に8個のクイーンをお互いに他の駒に取られないような位置においていきます。置き方は何通りあるのでしょうか?
縦列だけに注目すると同じ列にはひとつのクイーンしか置けません。そこで各列について上から何番目の位置にクイーンを置くかを数値で表し、要素数8の整数のリストをつくります。
また横列もひとつのクイーンしか置けません。ということは要素数8のリストのなかに同じ整数は含まれないということになります。1~8の順列を作って斜めのチェックをすれば答えを得ることができそうです。
以下は1~8の順列を得るためのメソッドです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
List<List<int>> CreatePermutations() { List<List<int>> ret = new List<List<int>>(); for(int i = 0; i < 8; i++) { List<int> vs1 = new List<int>(); vs1.Add(i); ret.Add(vs1); } for(int k = 1; k < 8; k++) { List<List<int>> temp = new List<List<int>>(); foreach(List<int> vs1 in ret) { for(int i = 0; i < 8; i++) { if(!vs1.Any(x => x == i)) { List<int> vs2 = vs1.ToList(); vs2.Add(i); temp.Add(vs2); } } } ret = temp; } return ret; } |
あとは斜めのラインだけチェックします。
各列に置かれているクイーンからみて取ることができるクイーンがあるかどうか調べます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
bool Check1(List<int> vs) { for(int x = 0; x < 8; x++) { int y = vs[x]; // 各列のクイーンについて取ることができるクイーンが存在するかどうか調べる if(!Check2(vs, x, y)) { return false; } } return true; } // (x,y)の位置にあるクイーンに取られるクイーンが存在するかどうか調べる bool Check2(List<int> vs, int x, int y) { for(int i = 1; x + i < 8; i++) { // (x,y)の位置にあるクイーンに取られるクイーンが存在する if(vs[x + i] == y + i || vs[x + i] == y - i) return false; } for(int i = 1; x - i >= 0; i++) { // (x,y)の位置にあるクイーンに取られるクイーンが存在する if(vs[x - i] == y + i || vs[x - i] == y - i) return false; } return true; } |
ボタンが押されたら処理を開始します。0~7までの順列をすべて取得します。これで縦横でお互い他のクイーンに取られることはない配置が得られますが、斜めはそうではないのでチェックします。解が得られたらリストに格納します。
解が格納されたリストを文字列に変換して結果を表示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
private void button1_Click(object sender, EventArgs e) { List<List<int>> vs = CreatePermutations(); List<List<int>> ret = new List<List<int>>(); foreach(List<int> vs5 in vs) { if(Check1(vs5)) ret.Add(vs5); } ShowResult(ret); } |
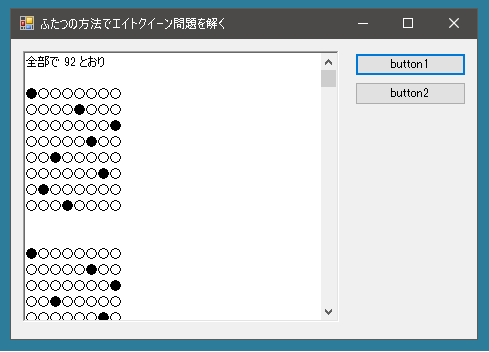
これは結果をリッチテキストボックスに表示するためのメソッドです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
void ShowResult(List<List<int>> vs) { StringBuilder sb = new StringBuilder(); sb.Append($"全部で {vs.Count()} とおり\n\n"); foreach(List<int> ints in vs) { string[] strs = ints.Select(x => x.ToString()).ToArray(); string str = String.Join(",", strs); foreach(int i in ints) { string str1 = "○○○○○○○○\n"; char[] chars = str1.ToArray(); chars[i] = '●'; str1 = new string(chars); sb.Append(str1); } sb.Append("\n\n"); } richTextBox1.Text = sb.ToString(); } |
この方法は斜めに取ることができるクイーンがある配置であってもとりあえず取得するという無駄な処理をしています。そこで一列ずつ置くことができる場所があるかどうか調べながら処理をします。置くことができない場合は、それ以上考えません。これで処理にかかる時間を短縮できるかもしれません。
GetPositionCanPut(List<int> vs)メソッドは、すでに要素が1以上存在するリストを渡して、クイーンを置くことができる位置のリストを求めるメソッドです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
List<int> GetPositionCanPut(List<int> vs) { List<int> ret = new List<int>(); List<int> rev = vs.ToList(); rev.Reverse(); int count = vs.Count; for(int i = 0; i < 8; i++) { if(vs.Any(x => x == i)) continue; int c = 0; bool b = true; foreach(int k in rev) { c++; if(k == i + c || k == i - c) { b = false; break; } } if(b) ret.Add(i); } return ret; } |
GetQueensPositions(List<int> parentList, List
|
1 2 3 4 5 6 7 8 9 10 11 |
List<List<int>> GetQueenPositions(List<int> queenPositions, List<int> newPositions) { List<List<int>> ret = new List<List<int>>(); foreach(int i in newPositions) { List<int> vs = queenPositions.ToList(); vs.Add(i); ret.Add(vs); } return ret; } |
ボタンが押されたら処理を開始します。
すでに置かれているクイーンに対して新しいクイーンを配置できる場所を調べて追加していきます。配置できない場合はその配置は捨てられます。最後に得られた結果をShowResultメソッドで表示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
private void button2_Click(object sender, EventArgs e) { List<List<int>> ret = GetResult(); ShowResult(ret); } List<List<int>> GetResult() { List<List<int>> ret = new List<List<int>>(); for(int i = 0; i < 8; i++) { List<int> vs = new List<int>(); vs.Add(i); ret.Add(vs); } while(true) { List<List<int>> newList = new List<List<int>>(); foreach(List<int> ints in ret) { List<int> vs = GetPositionCanPut(ints); newList.AddRange(GetQueenPositions(ints, vs)); } if(newList.Count == 0) return new List<List<int>>(); ret = newList; if(ret[0].Count == 8) return ret; } } |
実際に処理時間に違いはあるのでしょうか? ShowResultメソッドの部分は同じなので、それ以外の部分の処理にかかる時間を計測します。
前者では100ミリ秒以上かかりますが、後者であれば数ミリ秒で終わることがわかりました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
private void button1_Click(object sender, EventArgs e) { DateTime time1 = DateTime.Now; List<List<int>> vs = CreatePermutations(); List<List<int>> ret = new List<List<int>>(); foreach(List<int> vs5 in vs) { if(Check1(vs5)) ret.Add(vs5); } DateTime time2 = DateTime.Now; TimeSpan span = time2 - time1; Text = span.TotalMilliseconds.ToString(); ShowResult(ret); } private void button2_Click(object sender, EventArgs e) { DateTime time1 = DateTime.Now; List<List<int>> ret = GetResult(); DateTime time2 = DateTime.Now; TimeSpan span = time2 - time1; Text = span.TotalMilliseconds.ToString(); ShowResult(ret); } |
