C#で最小二乗法をつかって単回帰直線を引くプログラムを作成します。
単回帰分析がなにか? 単回帰分析の重要性に関してはこの動画がわかりやすいと思います。
たとえばマーケティングでは「獲得したデータを分析し、いかに将来の顧客行動を予測するか」が大切です。ここで獲得するデータは、ひとつではありません。アンケートデータや購買データ、Webの閲覧データなどがあります。他にもあるかもしれません。これは重回帰分析とよばれます。回帰分析は、データ分析による予測の基礎であります。
回帰分析のなかでも単回帰分析は1つの目的変数を1つの説明変数で予測するもので、1つの目的変数を1つの説明変数からY=aX+bという一次方程式の形で表します。Y=aX+bのa(傾き)とb(Y切片)がわかれば、両者の関係を予測することができるのです。
たとえば冷たい飲み物を売っている店があってその日の気温が高ければ冷たい飲み物もたくさん売れることは予想できます。これまでに蓄積してきた気温と売上のデータから明日の気温の予想ができれば用意すべき飲み物も量も予測できます。たくさん商品を用意しても売れ残ってしまえば捨てるしかありません。少なくしか商品を用意できないのであれば顧客を満足させることはできません。
お客さんがどれくらい来てどれくらい注文されるかは店の人にとっては重大な問題なのです。
ではこれまでの気温とこれまでの売上のデータから単回帰直線を引くにはどうすればいいのでしょうか? これに関しては最小二乗法という手法を用いるのですが、この手法に関しては以下の動画がわかりやすいと思います。
ではこの計算方法で単回帰直線を引くことを考えてみましょう。細かい計算法の説明は上の動画に委ねます。ここで説明されていることは、単回帰直線の傾きと切片(一次直線 y = ax + b の a の部分と b の部分)は以下のようにして計算されるのです。
a = {(xとyの積の平均値) – (xの平均値 * y平均値)} ÷ {(xの2乗の平均) – (xの平均値の2乗)}
b = – a * (xの平均値) + (yの平均値)
なぜこんな計算式になるのかは動画をみてください。
では実際に計算してみましょう。
XとYを格納するクラスDataを作成します。
|
1 2 3 4 5 |
public class Data { public int X = 0; public int Y = 0; } |
DataのインスタンスができたらDataのリストに格納します。
変数xの平均 AverageOfX、変数yの平均 AverageOfY、変数xとyの積の平均 AverageOfXY、変数xの2乗の平均 AverageOfSquareXとすると以下のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 |
// 変数 x の平均 double AverageOfX = (double)datas.Select(x => x.X).Sum() / datas.Count; // 変数 y の平均 double AverageOfY = (double)datas.Select(x => x.Y).Sum() / datas.Count; // 変数 x と y の積の平均 double AverageOfXY = (double)datas.Select(x => x.X * x.Y).Sum() / datas.Count; // 変数xの2乗の平均 double AverageOfSquareX = (double)datas.Select(x => x.X * x.X).Sum() / datas.Count; |
そして単回帰直線の傾きと切片を求めると以下のようになります。
|
1 2 3 4 5 |
// 単回帰直線の傾き double a = (AverageOfXY - AverageOfX * AverageOfY) / (AverageOfSquareX - AverageOfX * AverageOfX); // 単回帰直線の切片 double b = - a * AverageOfX + AverageOfY; |
これでaとb、すなわち単回帰直線の傾きと切片を求めることができます。
では適当なデータを入力して試運転してみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
List<Data> datas = new List<Data>(); datas.Add(new Data() { X = 10, Y = 10, }); datas.Add(new Data() { X = 4, Y = 5, }); datas.Add(new Data() { X = 2, Y = 5, }); datas.Add(new Data() { X = 2, Y = 4, }); datas.Add(new Data() { X = 8, Y = 4, }); datas.Add(new Data() { X = 9, Y = 6, }); datas.Add(new Data() { X = 7, Y = 6, }); datas.Add(new Data() { X = 5, Y = 2, }); datas.Add(new Data() { X = 1, Y = 1, }); datas.Add(new Data() { X = 3, Y = 2, }); datas.Add(new Data() { X = 4, Y = 7, }); datas.Add(new Data() { X = 6, Y = 7, }); datas.Add(new Data() { X = 8, Y = 9, }); datas.Add(new Data() { X = 11, Y = 8, }); datas.Add(new Data() { X = 6, Y = 4, }); // 変数 x の平均 double AverageOfX = (double)datas.Select(x => x.X).Sum() / datas.Count; // 変数 y の平均 double AverageOfY = (double)datas.Select(x => x.Y).Sum() / datas.Count; // 変数 x と y の積の平均 double AverageOfXY = (double)datas.Select(x => x.X * x.Y).Sum() / datas.Count; // 変数xの2乗の平均 double AverageOfSquareX = (double)datas.Select(x => x.X * x.X).Sum() / datas.Count; // 単回帰直線の傾き double a = (AverageOfXY - AverageOfX * AverageOfY) / (AverageOfSquareX - AverageOfX * AverageOfX); // 単回帰直線の切片 double b = -a * AverageOfX + AverageOfY; |
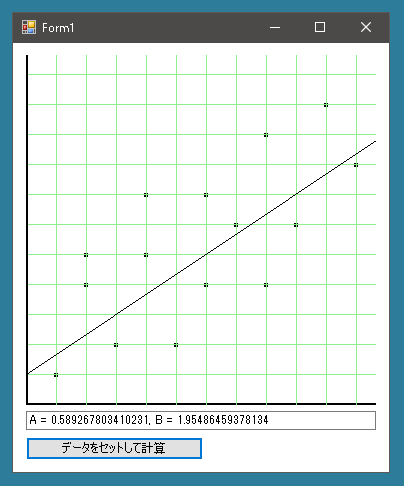
これで処理を実行すると、a = 0.589267803410231, b = 1.95486459378134になります。
これでグラフを作成してみます。最小値は0より大きく最大値は10より少し大きいです。そこで縦横350ピクセルのビットマップを作成してXとYの値を30倍してその座標に点を描画します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
// すでに a,bの値は取得されているものとする Bitmap bitmap = new Bitmap(350, 350); Graphics g = Graphics.FromImage(bitmap); pictureBox1.Size = new Size(350, 350); // 各座標に点を描画する データに30を書けた値をX,Y座標にする int rate = 30; foreach (Data data in datas) { int x = data.X * rate; int y = data.Y * rate; g.FillRectangle(new SolidBrush(Color.Black), new Rectangle(new Point(x-2, y-2), new Size(4, 4))); } // X軸とY軸を描画する // X軸 g.DrawLine(new Pen(Color.Black, 4), 0, 0, 350, 0); for (int y = 1; y < 15; y++) g.DrawLine(new Pen(Color.LightGreen), 0, y * rate, 350, y * rate); // Y軸 g.DrawLine(new Pen(Color.Black, 4), 0, 0, 0, 350); for (int x = 1; x < 15; x++) g.DrawLine(new Pen(Color.LightGreen), x * rate, 0, x * rate, 350); // y =ax + bの直線を描画する(傾きはそのままでよいが、切片は30倍しないといけない) int x0 = 0; int y0 = (int)b * rate; int x1 = bitmap.Width; int y1 = (int)(a * x1 + b * rate); g.DrawLine(new Pen(Color.Black), x0, y0, x1, y1); g.Dispose(); // Y座標が数学の座標とは逆なので上下反転させて数学座標と一致させる bitmap.RotateFlip(RotateFlipType.RotateNoneFlipY); pictureBox1.Image = bitmap; |
実行結果は以下のようになります。

