Contents
動的計画法で2項間漸化式を解く
漸化式とは数列を再帰的に定める等式です。ある項とそれ以前の項の関係がはっきりしているなら、各項の値を求めることができます。
2項間漸化式を解く
a_1 = 6,a_(n) = a_(n – 1) – 8 によって定められる数列{an}の一般項を求めよ。
高校の数学の知識があれば自分で計算することもできるのですが(特性方程式を使う問題ですね)、ここはプログラミングで解を導きます。
求めたい項の最大値よりも1以上大きな配列を用意します。先頭は0、初項に相当するa[1]には初項を代入します。あとは第n項とn-1項の関係がわかっているので順番に値を代入していきます。
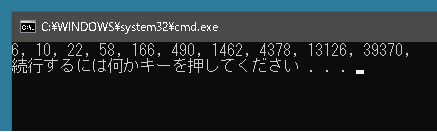
実行結果は以下のようになります。
6, 10, 22, 58, 166, 490, 1462, 4378, 13126, 39370,
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { int max = 10; int[] a = new int[max + 1]; // new int[max + 1] でよいが念のため大きめの数をいれている a[0] = 0; a[1] = 6; // 初項 for (int i = 2; i <= max; i++) { a[i] = 3 * a[i - 1] - 8; } for (int i = 1; i <= max; i++) Console.Write(a[i] + ", "); Console.WriteLine(); } } |
3項間漸化式
3項間漸化式であっても同様に求めることができます。ここではフィボナッチ数列を求めることにします。
フィボナッチ数列は a[1] == 1, a[2] == 1, a[1] == 1, n ≧ 3)のときは a[n] = a_[n – 2] + a[n – 1] です。そこで求めたい項の最大値よりも1以上大きな配列を用意して、そこに値を代入していきます。
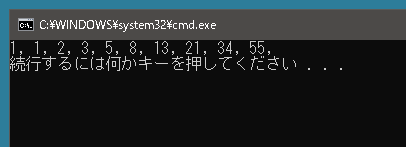
実行結果は 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, となります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { int max = 10; // 初項から第10項まで表示させる int[] fibonacci = new int[max + 10]; for (int i = 1; i <= max; i++) { if (i == 0) fibonacci[0] = 0; if (i == 1) fibonacci[1] = 1; else if (i == 2) fibonacci[2] = 1; else fibonacci[i] = fibonacci[i - 2] + fibonacci[i - 1]; } for (int i = 1; i <= max; i++) Console.Write(fibonacci[i] + ", "); Console.WriteLine(); } } |
階段の上り方
動的計画法で解く問題として「階段の上り方」があります。一歩で階段を1段上るのと2段上るのを組み合わせて、n 段の階段を上る方法は何通りあるのかを考える問題です。実際問題としては一歩で上れるのは3段が限界だと思うのですが、プログラミングの世界ではなんでもありです。10段同時上りとか普通にあります。
1歩で1段と2段の組み合わせ方は?
階段を上るのに、1 歩で 1 段または 2 段を上ることができるとき、n 段の階段を上る方法は何通りあるでしょうか。
階段が0段であればなにもしないのでこの場合は方法が1通りあると考えます。1段なら1とおり、2段なら2とおりあります。もし階段が n – 1 段以下のとき答えが分かっているとすれば n段のときはそれらを利用して求めることができます。
n 段目に到達するには、n-1 段目から1段上る方法と、n-2 段目から2段上る方法の2つがあります。したがって n段のときの答えは n-1 段目に到達できる方法とn-2 段目に到達できる方法のふたつを足した数ということになります。dp[0] = 1、dp[1] = 1、 dp[n] = dp[n – 1] + dp[n – 2] の漸化式を解けば答えを求めることができます。
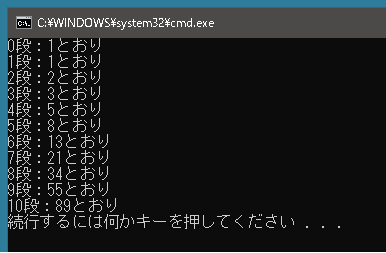
0段から10段まで何通りの上り方があるか表示させてみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static int GetResult(int n) { int[] arr = new int[n + 10]; arr[0] = 1; for (int i = 1; i <= n; i++) { arr[i] = 0; if (i - 1 >= 0) // arr[i - 1]がアクセス不可の場合があるので注意する arr[i] += arr[i - 1]; if (i - 2 >= 0) arr[i] += arr[i - 2]; } return arr[n]; } static void Main() { for (int i = 0; i <= 10; i++) Console.WriteLine($"{i}段:{GetResult(i)}とおり"); } } |
1歩でa段とb段の組み合わせ方は?
では1歩で a 段または b 段を上ることができるとき、n 段の階段を上る方法は何通りあるでしょうか。この場合、解が存在しない場合があります。全部で5段ある場合、1歩で3段上がるのと4段上がる組み合わせでは解が存在しません。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static int GetResult(int a, int b, int n) { int[] arr = new int[n + 10]; arr[0] = 1; for (int i = 1; i <= n; i++) { arr[i] = 0; if (i - a >= 0) arr[i] += arr[i - a]; if (i - b >= 0) arr[i] += arr[i - b]; } return arr[n]; } static void Main() { int a = 3; int b = 4; int n = 11; Console.WriteLine($"{a}段と{b}段の組み合わせで{n}段:{GetResult(a, b, n)}とおり"); a = 5; b = 3; n = 23; Console.WriteLine($"{a}段と{b}段の組み合わせで{n}段:{GetResult(a, b, n)}とおり"); a = 4; b = 3; n = 5; Console.WriteLine($"{a}段と{b}段の組み合わせで{n}段:{GetResult(a, b, n)}とおり"); } } |
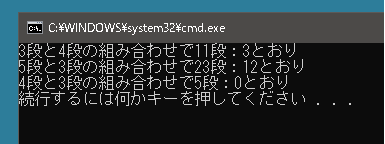
では1歩で a 段、 b 段、または c 段を上ることができる場合も、ちょっと変更を加えるだけで解は得られます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static int GetResult(int a, int b, int c, int n) { int[] arr = new int[n + 10]; arr[0] = 1; for (int i = 1; i <= n; i++) { arr[i] = 0; if (i - a >= 0) arr[i] += arr[i - a]; if (i - b >= 0) arr[i] += arr[i - b]; if (i - c >= 0) arr[i] += arr[i - c]; } return arr[n]; } static void Main() { int a = 3; int b = 4; int c = 5; int n = 11; Console.WriteLine($"{a}段と {a}段と {c}段の組み合わせで {n}段:{GetResult(a, b, c, n)}とおり"); a = 5; b = 3; c = 7; n = 23; Console.WriteLine($"{a}段と {a}段と {c}段の組み合わせで {n}段:{GetResult(a, b, c, n)}とおり"); a = 4; b = 3; c = 7; n = 5; Console.WriteLine($"{a}段と {a}段と {c}段の組み合わせで {n}段:{GetResult(a, b, c, n)}とおり"); } } |
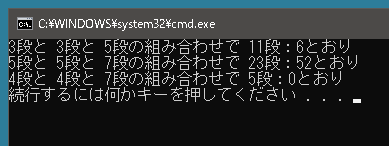
まとめ売りしているリンゴの買い方
りんごがまとめ売りをしています。必要な個数のリンゴを安く買うにはどのような組み合わせで買えばよいでしょうか?
ただし実際に買うりんごは 必要な個数を超えてもよいものとします。たとえば1個で150円、3個で250円、あわせて2個買うような場合は1個余分に買ってしまうことになりますが、3個で250円を買ったほうが安上がりです。
りんごのばら売りと2個のセット売り
八百屋でりんご1個が a 円で、りんご2個が b 円で売られています。このとき、n個のりんごを手に入れるために必要な金額の最小値はいくらでしょうか。
すでにn-1個のりんごを最も安く買うために必要な金額とn-2個のりんごを最も安く買うために必要な金額がわかっているとすれば、n-1 個のりんごを最も安く買ったうえで最後に1個のりんごを a 円で買う場合と、n-2 個のりんごを最も安く買ったうえで最後に2個のりんごを b 円で買う場合を考えて少ないほうが答えになることがわかります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static int GetCost(int n, int a, int b) { int[] arr = new int[n + 1]; arr[0] = 0; for (int i = 1; i <= n; i++) { if(i - 2 >= 0) arr[i] = Math.Min(arr[i - 1] + a, arr[i - 2] + b); else if (i - 1 >= 0) arr[i] = arr[i - 1] + a; } return arr[n]; } static void Main() { int n = 10; int a = 100; int b = 150; Console.WriteLine($"1個{a}円と2個{b}円"); for (int i = 0; i < n; i++) Console.WriteLine($"あわせて {i} 個:{GetCost(i, a, b)}円"); } } |
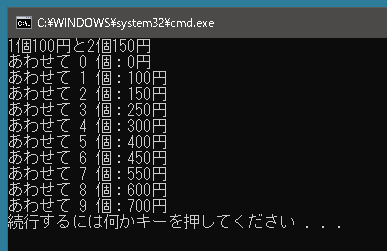
りんごの2個と5個のセット売り
次はりんご2個が a 円、5個が b 円で売られている場合を考えます。この場合、n 個のりんごを手に入れるために必要な金額の最小値はいくらでしょうか。実際に購入するりんごの個数は n を超えてもよいものとします。
前問では「1個と2個」だったものが「2個と5個」に変わりました。前問と同じ方法で以下のようなコードを書くとただしい解が得られません。これは3個のりんごをちょうど買う方法が存在しないからです。また4個買うより5個買うほうが安いという珍現象も発生しています。以下はまちがったやり方です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
public class Program { static int GetCostWrong() { int n = 10; int a = 110; int b = 200; int[] arr = new int[n + 1]; arr[0] = 0; for (int i = 1; i < arr.Length; i++) { if (i - 5 >= 0) arr[i] = Math.Min(arr[i - 2] + a, arr[i - 5] + b); else if (i - 2 >= 0) arr[i] = arr[i - 2] + a; } for (int i = 1; i < arr.Length; i++) Console.WriteLine($"{i}個 {arr[i]}円"); return arr[n]; } } |
実行結果
|
1 2 3 4 5 |
1個 0円 // 正しくない 正しい値は 110 2個 110円 3個 110円 // 正しくない 正しい値は 200 4個 220円 // 正しくない 正しい値は 200 5個 200円 |
これだと正しい解を求めることができます。ただ面倒くさいです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
public class Program { static int GetCost() { int n = 10; int a = 110; int b = 200; int[] arr = new int[n + 1]; arr[0] = 0; for (int i = 1; i < arr.Length; i++) { List<int> costs = new List<int>(); if(i - 1 >= 0) costs.Add(arr[i - 1] + a); if (i - 2 >= 0) costs.Add(arr[i - 2] + a); if (i - 3 >= 0) { costs.Add(arr[i - 3] + a * 2); costs.Add(arr[i - 3] + b); } if (i - 4 >= 0) { costs.Add(arr[i - 4] + a * 2); costs.Add(arr[i - 4] + b); } if (i - 5 >= 0) { costs.Add(arr[i - 5] + a * 3); costs.Add(arr[i - 5] + b); } arr[i] = costs.Min(); } for (int i = 1; i < arr.Length; i++) Console.WriteLine($"{i}個 {arr[i]}円"); return arr[n]; } } |
実行結果
|
1 2 3 4 5 6 7 8 9 10 |
1個 110円 2個 110円 3個 200円 4個 200円 5個 200円 6個 310円 7個 310円 8個 400円 9個 400円 10個 400円 |
上の書き方より下のように書いたほうがすっきりしているし、拡張性もあります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
public class Program { static int GetCostNice(int n, int a, int b) { int[] arr = new int[n + 5]; for (int i = 1; i < n + 5; i++) arr[i] = int.MaxValue / 2; // int.MaxValueだとオーバーフローするので対策 arr[0] = 0; for (int i = 1; i < n + 5; i++) { if (i >= 2) arr[i] = Math.Min(arr[i], arr[i - 2] + a); if (i >= 5) arr[i] = Math.Min(arr[i], arr[i - 5] + b); } // arr[i]よりもarr[k](ただし k は i + 1 以上 i + 4 以下の範囲のみ調べる)の値が少ない場合は変更する int[] arr2 = new int[n + 5]; for (int i = n + 4; i >= 1; i--) { arr2[i] = arr[i]; for (int k = i + 1; k < n + 5; k++) arr2[i] = Math.Min(arr2[i], arr[k]); } return arr2[n]; } static void Main() { int n = 10; int a = 100; int b = 150; Console.WriteLine($"2個{a}円と5個{b}円"); for (int i = 0; i <= n; i++) Console.WriteLine($"あわせて {i} 個:{GetCostNice(i, a, b)}円"); } } |
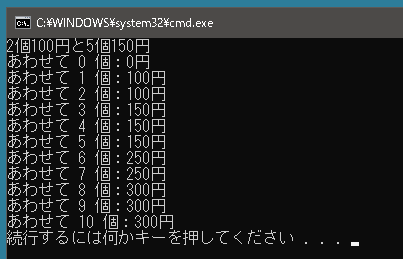
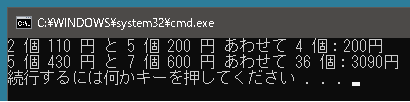
以下のコードであれば「りんご x 個が a 円で、りんご y 個が b 円で売られています」という問題にも対応できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static int GetCost(int n, int x, int a, int y, int b) { int xyMax = Math.Max(x, y); int[] arr = new int[n + xyMax]; for (int i = 1; i < n + xyMax; i++) arr[i] = int.MaxValue / 2; // int.MaxValueだとオーバーフローするので対策 arr[0] = 0; for (int i = 1; i < n + xyMax; i++) { if (i >= x) arr[i] = Math.Min(arr[i], arr[i - x] + a); if (i >= y) arr[i] = Math.Min(arr[i], arr[i - y] + b); } int[] arr2 = new int[n + xyMax]; for (int i = n + xyMax - 1; i >= 1; i--) { arr2[i] = arr[i]; for (int k = i + 1; k < n + xyMax; k++) arr2[i] = Math.Min(arr2[i], arr[k]); } return arr2[n]; } static void Main() { int n = 4; int x = 2; int a = 110; int y = 5; int b = 200; int cost = GetCost(n, x, a, y, b); Console.WriteLine($"{x} 個 {a} 円 と {y} 個 {b} 円 あわせて {n} 個:{cost}円"); n = 36; x = 5; a = 430; y = 7; b = 600; cost = GetCost(n, x, a, y, b); Console.WriteLine($"{x} 個 {a} 円 と {y} 個 {b} 円 あわせて {n} 個:{cost}円"); } } |