Contents
区間の総和を高速で求める累積和
累積和とは配列の任意の区間の総和を求めるためのアルゴリズムです。 繰り返し処理を使うと大きな計算量になってしまう区間の計算問題を、適切な前処理を行うことによって高速に行うことができます。
配列内の区間 [x0, y0], [x1, y1], [x2, y2], … [x1000, y1000] の総和をそれぞれ計算しなければならないときに便利です。
まず配列 A の A[0] ~ A[k] までの総和を 配列 B に格納します。A[0] ~ A[k] までの総和を B[k + 1] とします。また B[0] は 0 です。
区間 [x, y] の総和を計算するときは B[y + 1] – B[x] を計算します。これなら計算量は O(1) となります。
【連続する N 個の和の最大値】 連続する N 個の和の最大値 4 (paizaランク C 相当)
【連続する N 個の和の最大値】 連続する N 個の和の最大値 4 (paizaランク C 相当)
1 行目に整数 N, K が与えられます。
2 行目に N 個の整数 a_0, a_1, a_2, …, a_(N-1) が与えられます。
連続する K 個の整数の和の最大値を、累積和を使うことで求め、一行で出力してください。入力されるデータ
N K
a_0 a_1 a_2 … a_(N-1)
K ≦ N ≦ 100
ただし 1 ≦ K ≦ N, 1 ≦ a_i ≦ 100
長さ K の区間の総和をすべて計算し最大値を求めます。A[x] ~ A[x + k – 1] の総和を何度も計算することになるので累積和を用いると短時間で処理が完了します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N, K; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; K = vs[1]; } int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int[] sums = new int[N + 1]; for (int i = 0; i < N; i++) sums[i + 1] = sums[i] + A[i]; int ans = 0; for (int i = 0; i + K - 1 < N; i++) { int sum = sums[i + K] - sums[i]; ans = Math.Max(ans, sum); } Console.WriteLine(ans); } } |
二次元配列の累積和
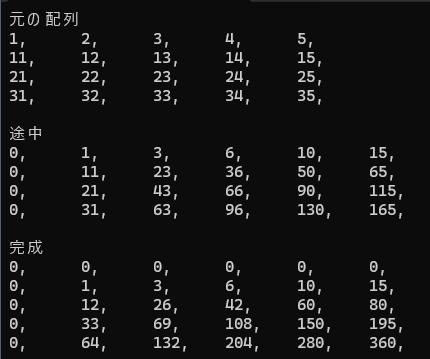
二次元配列の場合はどうなるでしょうか? 二次元配列の累積和はまず横の累積和を求め、そのあと縦の累積和を求めます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
class Program { static void Main() { int[,] A = { { 1, 2, 3, 4, 5}, {11, 12, 13, 14, 15}, {21, 22, 23, 24, 25}, {31, 32, 33, 34, 35}, }; ShowArray(A, "元の配列"); // この二次元配列に累積和が格納される int yMax = A.GetLength(0); int xMax = A.GetLength(1); int[,] sums1 = new int[yMax, xMax + 1]; for (int y = 0; y < yMax; y++) { for (int x = 0; x < xMax; x++) { sums1[y, x + 1] = sums1[y, x] + A[y, x]; } } ShowArray(sums1, "途中"); int[,] sums2 = new int[yMax + 1, xMax + 1]; for (int x = 0; x <= xMax; x++) { for (int y = 0; y < yMax; y++) sums2[y + 1, x] = sums2[y, x] + sums1[y, x]; } ShowArray(sums2, "完成"); } // デバッグ用 static void ShowArray(int[,] arr, string str) { Console.WriteLine(str); for (int y = 0; y < arr.GetLength(0); y++) { for (int x = 0; x < arr.GetLength(1); x++) Console.Write(arr[y, x] + ",\t"); Console.WriteLine(); } Console.WriteLine(); } } |
ただこのやり方はあまりよくありません。二次元配列の累積和があるなら三次元配列の累積和だってあるはずです。拡張性を考えたとき、もっと効率がよいやり方があります。
sums[y + 1, x + 1] を計算するときには、それよりも添え字が小さい部分の値は確定しています。だからその値を利用したいのですが、単に A[y, x] と sums[y + 1, x] と sums[y, x + 1] を加算するだけではうまくいきません。これは sums[y, x] を2回カウントしてしまっています。sums[y + 1, x + 1] = sums[y + 1, x] + sums[y, x + 1] – sums[y, x] + A[y, x] とするのが正しいです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
class Program { static void Main() { int[,] A = { { 1, 2, 3, 4, 5}, {11, 12, 13, 14, 15}, {21, 22, 23, 24, 25}, {31, 32, 33, 34, 35}, }; int yMax = A.GetLength(0); int xMax = A.GetLength(1); int[,] sums = new int[yMax + 1, xMax + 1]; for (int y = 0; y < yMax; y++) { for (int x = 0; x < xMax; x++) sums[y + 1, x + 1] = sums[y + 1, x] + sums[y, x + 1] - sums[y, x] + A[y, x]; } } } |
二次元配列 A の A[y1, x1] から A[y2, x2] で囲まれる部分の総和を求めるときは sums[y2 + 1, x2 + 1] から sums[y1, x2 + 1] と sums[y2 + 1, x1] を引きます。これだと二重に引いてしまう部分ができるので sums[y1, x1] を足します。
二次元累積和 4 (paizaランク C 相当)
1 行目に整数 a, b, c, d が与えられます。2 行目以降に 5 行 5 列の整数の二次元配列 A が与えられます。A の i 行目 j 列目を A_{i, j} (0 ≦ i ≦ 4, 0 ≦ j ≦ 4) と表すことにします。
長方形領域の左上の要素を A_{a, b} 、右下の要素を A_{c, d} としたとき、この長方形領域内の整数の和を累積和を用いて求め、一行で出力してください。
入力されるデータ
a b c d
A_{0, 0} A_{0, 1} A_{0, 2} A_{0, 3} A_{0, 4}
A_{1, 0} A_{1, 1} A_{1, 2} A_{1, 3} A_{1, 4}
A_{2, 0} A_{2, 1} A_{2, 2} A_{2, 3} A_{2, 4}
A_{3, 0} A_{3, 1} A_{3, 2} A_{3, 3} A_{3, 4}
A_{4, 0} A_{4, 1} A_{4, 2} A_{4, 3} A_{4, 4}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int a, b, c, d; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); a = vs[0]; b = vs[1]; c = vs[2]; d = vs[3]; } int[,] A = new int[5, 5]; for (int y = 0; y < 5; y++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); for (int x = 0; x < 5; x++) A[y, x] = vs[x]; } int yMax = A.GetLength(0); int xMax = A.GetLength(1); int[,] sums = new int[yMax + 1, xMax + 1]; for (int y = 0; y < yMax; y++) { for (int x = 0; x < xMax; x++) sums[y + 1, x + 1] = sums[y + 1, x] + sums[y, x + 1] - sums[y, x] + A[y, x]; } int ans = sums[c + 1, d + 1] - sums[a, d + 1] - sums[c + 1, b] + sums[a, b]; Console.WriteLine(ans); } } |
三次元累積和
では3次元累積和はどのように計算すればよいでしょうか? 累積和を計算するときは
sums[x + 1, y + 1, z + 1] =
+ (sums[x, y + 1, z + 1] + sums[x + 1, y, z + 1] + sums[x + 1, y + 1, z])
– (sums[x + 1, y, z] + sums[x, y + 1, z] + sums[x, y, z + 1])
+ sums[x, y, z] + A[x, y, z];
です。添字に + が偶数個あれば +、奇数個であれば – です。二次元配列のときと + と – が入れ替わっています。これは配列の次元の偶奇で入れ替わります。
A[x1, y1, z1] と A[x2, y2, z2] (ただし x1 ≦ x2, y1 ≦ y2, z1 ≦ z2)で囲まれる要素の総和ですが、これは
sums[x2 + 1, y2 + 1, z2 + 1]
– (sums[x1, y2 + 1, z2 + 1] + sums[x2 + 1, y1, z2 + 1] + sums[x2 + 1, y2 + 1, z1])
+ (sums[x1, y1, z2 + 1] + sums[x1, y2 + 1, z1] + sums[x2 + 1, y1, z1])
– sums[x1, y1, z1];
で求めることができます。
D – Cuboid Sum Query
これは3次元累積和の問題です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N = int.Parse(Console.ReadLine()); long[,,] A = new long[N, N, N]; for (int x = 0; x < N; x++) { for (int y = 0; y < N; y++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); for (int z = 0; z < N; z++) A[x, y, z] = vs[z]; } } long[,,] sums = new long[N + 1, N + 1, N + 1]; for (int x = 0; x < N; x++) { for (int y = 0; y < N; y++) { for (int z = 0; z < N; z++) { sums[x + 1, y + 1, z + 1] = + (sums[x, y + 1, z + 1] + sums[x + 1, y, z + 1] + sums[x + 1, y + 1, z]) - (sums[x + 1, y, z] + sums[x, y + 1, z] + sums[x, y, z + 1]) + sums[x, y, z] + A[x, y, z]; } } } int Q = int.Parse(Console.ReadLine()); List<long> rets = new List<long>(); for (int i = 0; i < Q; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int lx = vs[0] - 1; int rx = vs[1] - 1; int ly = vs[2] - 1; int ry = vs[3] - 1; int lz = vs[4] - 1; int rz = vs[5] - 1; rx++; ry++; rz++; long ans = sums[rx,ry, rz] - (sums[lx, ry, rz] + sums[rx, ly, rz] + sums[rx, ry, lz]) + (sums[lx, ly, rz] + sums[lx, ry, lz] + sums[rx, ly, lz]) - sums[lx, ly, lz]; rets.Add(ans); } foreach(long ret in rets) Console.WriteLine(ret); } } |
