両端キュー
両端キューまたはデックは、計算機科学における抽象データ型の1つで、先頭または末尾で要素を追加・削除できるキューです。
C – pushpush
長さ N の数列 A_1, A_2, …, A_N が与えられます。 空の数列 B に対して、以下の操作を N 回行うことを考えます。
i 回目には 数列の i 番目の要素 A_i を B の末尾に追加する。
B を逆向きに並び替える。この操作をしてできる数列 B を求めて下さい。
入力されるデータ
N
A_1 A_2 … A_N
(ただし 1 ≦ N ≦ 2×10^5, 0 ≦ A_i ≦ 10^9 )
実際に要素 A_i を B の末尾に追加するたびに B を反転していては制限時間内に間に合いません。そこでこう考えます。
偶数回目に追加するときは B の末尾に追加して、奇数回に追加するときは先頭に追加する
全部で奇数回追加した場合は B を反転したものを出力する
こうすることで反転処理を省略することができるので制限時間内に処理を完了することができます。ただC#には両端キューはないみたいなので普通のListを使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { int N = int.Parse(Console.ReadLine()); int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); List<int> list = new List<int>(); for (int i = 0; i < N; i++) { if(i % 2 == 0) list.Add(A[i]); else list.Insert(0, A[i]); } if(N % 2 == 1) list.Reverse(); Console.WriteLine(string.Join(" ", list)); } } |
これでも制限時間内には間に合うのですが、Listに何回もInsertすると処理に時間がかかります。List.Insertの計算量は O(N)です。代わりにLinkedListを使うとそのぶん高速になります。LinkedList.AddFirst や AddLast の計算量は O(1)です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
public class Program { static void Main() { int N = int.Parse(Console.ReadLine()); int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); LinkedList<int> linkedList = new LinkedList<int>(); for (int i = 0; i < N; i++) { if (i % 2 == 0) linkedList.AddLast(A[i]); else linkedList.AddFirst(A[i]); } List<int> list = linkedList.ToList(); if (N % 2 == 1) list.Reverse(); Console.WriteLine(string.Join(" ", list)); } } |
スライド最大値(最小値)
区間の最大値(最小値)を高速に求めたいとき両端キューが使えます。
この説明はわかりやすいです。
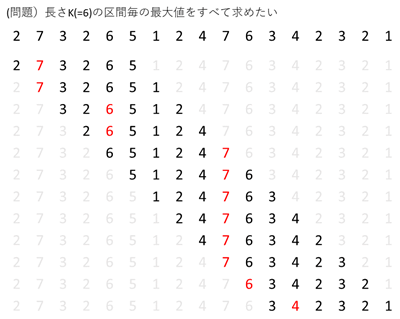
長さ6の区間ごとの最大値を求めたい場合、最初は[0, 5]で開始し、[1, 6]へ遷移するときはA[6]を追加し、A[0]を取り除く、[a, a + 5]から[a + 1, a + 6]へ遷移するときはA[a + 6]を追加し、A[a]を取り除く操作を繰り返します。
また区間の最大値を求める場合、自分より大きな値が入ってきたらその値は最大値になる可能性は消えます。そこで最大値になるかもしれない値の待ち行列をつくります。先頭が最大値です。そして先頭が区間のなかから消えるときは先頭を待ち行列から取り除きます。また区間に新しい値が入ってきたときに待ち行列のなかにそれよりも小さな値がある場合、その値は最大値になる可能性はなくなるので待ち行列から削除します。
先頭が区間のなかから消えるときは左から削除、待ち行列のなかに新しく入ってきた値よりも小さな値がある場合は右側から削除です。つまり両端キューが使えるわけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
using System; using System.Collections.Generic; using System.Linq; // 配列のインデックスと値をセットで扱えるようにする class Pair { public Pair(int index , int value) { Index = index; Value = value; } public int Index = 0; public int Value = 0; } public class Program { static void Main() { int[] A = { 2, 7, 3, 2, 6, 5, 1, 2, 4, 7, 6, 3, 4, 2, 3, 2, 1, }; int N = A.Length; int K = 6; LinkedList<Pair> linkedList = new LinkedList<Pair>(); for (int i = 0; i < N; i++) { Pair pair = new Pair(i, A[i]); // 新しく入ってきた値よりも末尾の値のほうが小さい場合はRemoveLastを繰り返す while (linkedList.Count > 0 && linkedList.Last.Value.Value < A[i]) linkedList.RemoveLast(); linkedList.AddLast(pair); // 先頭が区間から出ていく場合は先頭を取り除く if (i - K == linkedList.First.Value.Index) linkedList.RemoveFirst(); if (i >= K - 1) { // 待ち行列の内容を出力する(デバッグ用) Console.WriteLine(string.Join(", ", linkedList.ToArray().Select(_ => _.Value))); // 選択されている区間と最大値を出力する Console.WriteLine($"[{i - K + 1}, {i}] MAX = {linkedList.First.Value.Value}"); } } } } |
