エイホ-コラシック法辞書に登録したパターンは文字列内に存在するか？

エイホ-コラシック法（英: Aho-Corasick algorithm）とは、1975年にアルフレッド・エイホと Margaret J. Corasick が発見した文字列探索アルゴリズムです。

Contents

1 トライ木をもちいた文字列の検索
- 1.1 文字列のなかに登録された文字は存在するか？
2 PMA の構築
- 2.1 パターンが複数の場合のパターンマッチング
- 2.2 PMA の構築の高速化

トライ木をもちいた文字列の検索

トライ木は文字列の集合を索引化し、高速な検索を可能にするデータ構造です。

次の図は 5 つの文字列 “ab”, “abcd”, “bc”, “bab”, “d” を格納したトライ木を表します。頂点が赤いことは頂点のメンバ変数 is_end が true であることを意味します。

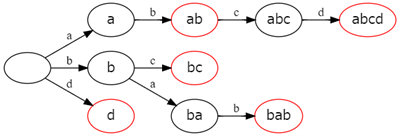
トライ木にある文字列が格納されているかを判定したいときには、根から S が格納されている頂点までたどり着くことができて、その頂点の is_end が true であることを確認すればよいです。トライ木はある文字列 S が格納されているかを O(S の長さ) で判定することができます。

public class Node
{
    public Node(string s)
    {
        S = s;
        IsEnd = false;
    }

    public bool IsEnd = false;
    public string S { get; }
    public Dictionary<char, Node> Nexts = new Dictionary<char, Node>();
}

public class Trie
{
    Node Root = new Node("");

    // 文字列 word をトライ木に格納する
    public void Insert(string word)
    {
        char[] vs = word.ToArray();
        Node cur = Root;
        foreach (char c in vs)
        {
            if (!cur.Nexts.ContainsKey(c))
                cur.Nexts.Add(c, new Node(cur.S + c));
            cur = cur.Nexts[c];
        }
        cur.IsEnd = true;
    }

    // 文字列 word がトライ木に格納されているかを調べる
    public bool Search(string word)
    {
        char[] vs = word.ToArray();
        Node cur = Root;
        foreach (char c in vs)
        {
            if (!cur.Nexts.ContainsKey(c))
                return false;
            cur = cur.Nexts[c];
        }
        if(cur.IsEnd)
            return true;
        else
            return false;
    }
}

public class Node

{

public Node(string s)

{

S = s;

IsEnd = false;

}

public bool IsEnd = false;

public string S { get; }

public Dictionary<char, Node> Nexts = new Dictionary<char, Node>();

}

public class Trie

{

Node Root = new Node("");

// 文字列 word をトライ木に格納する

public void Insert(string word)

{

char[] vs = word.ToArray();

Node cur = Root;

foreach (char c in vs)

{

if (!cur.Nexts.ContainsKey(c))

cur.Nexts.Add(c, new Node(cur.S + c));

cur = cur.Nexts[c];

}

cur.IsEnd = true;

}

// 文字列 word がトライ木に格納されているかを調べる

public bool Search(string word)

{

char[] vs = word.ToArray();

Node cur = Root;

foreach (char c in vs)

{

if (!cur.Nexts.ContainsKey(c))

return false;

cur = cur.Nexts[c];

}

if(cur.IsEnd)

return true;

else

return false;

}

文字列のなかに登録された文字は存在するか？

完全一致ではなく連続部分文字列であればどうでしょうか？

文字列 “abxstu” の連続部分文字列に “abc”, “xyz”, “stu” のいずれかがあるか調べるのであれば、新たに Trie.Search2メソッドを定義することでうまくできそうです。

public class Trie
{
    public bool Search2(string word)
    {
        char[] vs = word.ToArray();

        // 開始部分をひとつずつずらして調べる
        for (int start = 0; start < word.Length; start++)
        {
            Node cur = Root;
            for (int i = start; i < word.Length; i++)
            {
                char c = vs[i];
                if (!cur.Nexts.ContainsKey(c))
                    break;
                cur = cur.Nexts[c];
                if (cur.IsEnd)
                    return true;
            }
        }
        return false;
    }
}

class Program
{
    static void Main()
    {
        Trie trie = new Trie();

        trie.Insert("abc");
        trie.Insert("xyz");
        trie.Insert("stu");

        string T = "abxstu";
        if (trie.Search2(T))
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");
    }
}

public class Trie

{

public bool Search2(string word)

{

char[] vs = word.ToArray();

// 開始部分をひとつずつずらして調べる

for (int start = 0; start < word.Length; start++)

{

Node cur = Root;

for (int i = start; i < word.Length; i++)

{

char c = vs[i];

if (!cur.Nexts.ContainsKey(c))

break;

cur = cur.Nexts[c];

if (cur.IsEnd)

return true;

}

return false;

}

class Program

{

static void Main()

{

Trie trie = new Trie();

trie.Insert("abc");

trie.Insert("xyz");

trie.Insert("stu");

string T = "abxstu";

if (trie.Search2(T))

Console.WriteLine("Yes");

else

Console.WriteLine("No");

}

PMA の構築

ところが実はもっとうまい方法があります。

文字列 S を格納した頂点から S を除く接尾辞の中でグラフ内に存在する最長の文字列 T の対応する頂点へ failure と呼ばれる有向辺を追加します。また根は全ての文字に対する遷移が定義されている必要があります。定義されていない文字に対しては自己ループとなる遷移を定義します。

接尾辞とは長さ N の文字列であれば先頭 x (0 ≦ x ≦ N) 文字を削った文字列のことです。例えば “abc” の接尾辞は “abc”, “bc”, “c”, “” (長さ 0 の文字列) の 4 つです。ただしここでは「S を除く接尾辞の中で」という条件があるので “bc”, “c”, “” となります。

上に示したトライ木の各頂点に対して failure を追加すると図のようになります。青い有向辺が failure です。

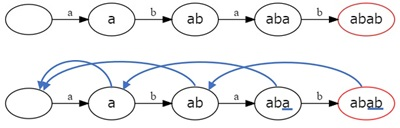
failure はパターンマッチングを効率よくできるようになります。パターンとする文字列を S、パターンが含まれているかを調べたい文字列を T とすると、その計算量は O(|T| × |S|)でした。これを O(|T|)で判定することができるようになります。

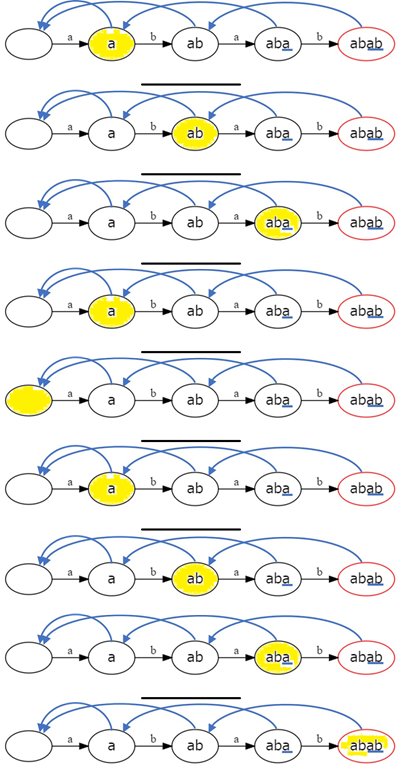
“abaabab” でパターンマッチングをおこないます。このとき PMA 上を次の表のように移動しています。

テキストの 1～3 文字目までを読み込ませた場合、頂点 aba に移動します。

テキストの 4 文字目 ‘a’ を読み込ませます。今いる頂点 aba には ‘a’ による遷移が定義されていないため、failure で頂点 a に遷移します。

頂点 a にも ‘a’ による遷移が定義されていないのでさらに failure で遷移をおこないます。遷移先の根には ‘a’ による遷移が定義されているので、この遷移によって頂点 a へと遷移します。

それ以降は 5～7 文字目までを順番に読み込むことで、頂点 abab まで移動することができます。

パターンが複数の場合のパターンマッチング

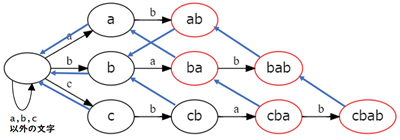
パターンが複数の場合も、おなじように failure を引けばよいのですが、これだけでは不完全です。例えば、”cba” というテキストに対して上手くいきません。テキスト “cba” に対するパターンマッチングでは “ba” というパターンを検知しなければならないのですが、頂点 cba の is_end が true ではないためうまくいきません。

頂点 cba の対応する文字列も “ba” を含むことから頂点 cba の is_end も true にしなければなりません。これは failure の先の頂点の is_end が true なら、自身の is_end も true でなければならないことを意味しています。そしてこの処理が正しくおこなわれるためには根に近い頂点から順に failure を引かなければなりません。そうしないと failure を引いた先の頂点の is_end があとになって true に変化したときに対応できなくなります。

これらを踏まえると正しい PMA は次の図のようになります。

PMA の構築の高速化

上記の方法をそのまま実行しようとすると、ある頂点の failure の行先を調べるにはその対応する文字列の接尾辞をすべて調べる必要がありました。しかし処理を高速化させるうまい方法があります。

failure には以下のような関係があります。

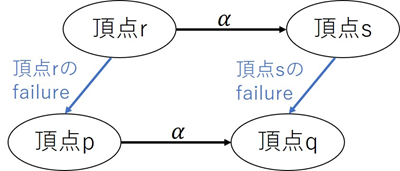
この図は r の接尾辞に α を付け足した文字列 s の接尾辞 q は、r の接尾辞 p に α を付け足した文字列 q となりえることを示しています。

ではこの場合はどうでしょうか？

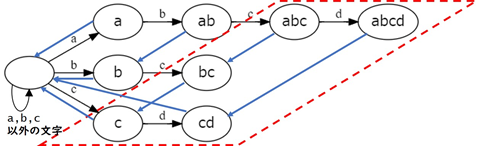
頂点 abcd の failure の行き先を探す方法を考えます。頂点 abcd が頂点 s 、頂点 abc が頂点 r に相当します。このとき p に相当する頂点を探したいのですが、頂点 abc から failure で遷移した頂点 bc には文字 d による遷移が定義されていません。そこで頂点 bc からさらにfailure による遷移をおこなうと、頂点 c にたどり着きます。この頂点には文字 d による遷移が定義されているので、頂点 c が p 、頂点 cd が q となり、頂点 cd が頂点 abcd からの failure の行先となります。

このように頂点 p は頂点 r から failure による遷移を繰り返して到達できる頂点の中で、文字 α による遷移が定義されている最初の頂点となります。「最初の」とするのは q が、p の接尾辞のうち最長のものという failure の引き方の条件を満たすようにするためです。

以上のことから Aho-Corasick 法で PMA を構築するコートを書くと以下のようになります。

using System;
using System.Collections.Generic;
using System.Linq;

class Node
{
    public Node(string s)
    {
        S = s;
        IsEnd = false;
    }

    public string S { get; }
    public bool IsEnd = false;
    public Dictionary<char, Node> Nexts = new Dictionary<char, Node>();
    public Node Failure = null;
}

class AhoCorasick
{
    Node Root = new Node("");
    List<Node> Nodes = new List<Node>();

    public AhoCorasick()
    {
    }

    // パターンとなる文字列を格納する
    public void Insert(string pattern)
    {
        char[] vs = pattern.ToArray();
        Node cur = Root;
        foreach (char c in vs)
        {
            if (!cur.Nexts.ContainsKey(c))
            {
                Node node = new Node(cur.S + c);
                cur.Nexts.Add(c, node);
                Nodes.Add(node);
            }
            cur = cur.Nexts[c];
        }
        cur.IsEnd = true;
    }

    // failure を適切に引くことで PMA を構築する
    public void Build()
    {
        Root.Failure = Root;

        Nodes = Nodes.OrderBy(_ => _.S.Length).ToList();
        List<Node> firstNodes = Nodes.Where(_ => _.S.Length == 1).ToList();

        foreach (Node node in firstNodes)
            node.Failure = Root;

        foreach (Node node in Nodes)
        {
            foreach (var pair in node.Nexts)
            {
                Node next = pair.Value;
                Node cur = node;

                while (true)
                {
                    Node failure = cur.Failure;
                    if (failure.Nexts.ContainsKey(pair.Key))
                    {
                        next.Failure = failure.Nexts[pair.Key];
                        if (failure.Nexts[pair.Key].IsEnd)
                            node.IsEnd = true;
                        break;
                    }
                    else
                    {
                        if (failure == Root)
                        {
                            next.Failure = Root;
                            break;
                        }
                        else
                            cur = failure;
                    }
                }
            }
        }
    }

    // 構築した PMA を用いてパターンマッチングをおこなう
    public bool Match(string text)
    {
        char[] vs = text.ToArray();
        Node cur = Root;

        for (int i = 0; i < vs.Length;)
        {
            char c = vs[i];
            if (cur.Nexts.ContainsKey(c))
            {
                cur = cur.Nexts[c];
                i++;
                if (cur.IsEnd)
                    return true;
            }
            else
            {
                if (cur == Root)
                    i++;
                else
                    cur = cur.Failure;
            }
        }
        return false;
    }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

using System;

using System.Collections.Generic;

using System.Linq;

class Node

{

public Node(string s)

{

S = s;

IsEnd = false;

}

public string S { get; }

public bool IsEnd = false;

public Dictionary<char, Node> Nexts = new Dictionary<char, Node>();

public Node Failure = null;

}

class AhoCorasick

{

Node Root = new Node("");

List<Node> Nodes = new List<Node>();

public AhoCorasick()

{

}

// パターンとなる文字列を格納する

public void Insert(string pattern)

{

char[] vs = pattern.ToArray();

Node cur = Root;

foreach (char c in vs)

{

if (!cur.Nexts.ContainsKey(c))

{

Node node = new Node(cur.S + c);

cur.Nexts.Add(c, node);

Nodes.Add(node);

}

cur = cur.Nexts[c];

}

cur.IsEnd = true;

}

// failure を適切に引くことで PMA を構築する

public void Build()

{

Root.Failure = Root;

Nodes = Nodes.OrderBy(_ => _.S.Length).ToList();

List<Node> firstNodes = Nodes.Where(_ => _.S.Length == 1).ToList();

foreach (Node node in firstNodes)

node.Failure = Root;

foreach (Node node in Nodes)

{

foreach (var pair in node.Nexts)

{

Node next = pair.Value;

Node cur = node;

while (true)

{

Node failure = cur.Failure;

if (failure.Nexts.ContainsKey(pair.Key))

{

next.Failure = failure.Nexts[pair.Key];

if (failure.Nexts[pair.Key].IsEnd)

node.IsEnd = true;

break;

}

else

{

if (failure == Root)

{

next.Failure = Root;

break;

}

else

cur = failure;

}

// 構築した PMA を用いてパターンマッチングをおこなう

public bool Match(string text)

{

char[] vs = text.ToArray();

Node cur = Root;

for (int i = 0; i < vs.Length;)

{

char c = vs[i];

if (cur.Nexts.ContainsKey(c))

{

cur = cur.Nexts[c];

i++;

if (cur.IsEnd)

return true;

}

else

{

if (cur == Root)

i++;

else

cur = cur.Failure;

}

return false;

}

実際に使ってみます。ここでは “caababa” のなかにパターン “bab”, “cbab” があるかを調べています。

class Program
{
    static void Main()
    {
        AhoCorasick ahoCorasick = new AhoCorasick();
        ahoCorasick.Insert("bab");
        ahoCorasick.Insert("cbab");

        ahoCorasick.Build();

        string T = "caababa";
        if (ahoCorasick.Match(T))
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");
    }
}

class Program

{

static void Main()

{

AhoCorasick ahoCorasick = new AhoCorasick();

ahoCorasick.Insert("bab");

ahoCorasick.Insert("cbab");

ahoCorasick.Build();

string T = "caababa";

if (ahoCorasick.Match(T))

Console.WriteLine("Yes");

else

Console.WriteLine("No");

}

エイホ-コラシック法辞書に登録したパターンは文字列内に存在するか？

トライ木をもちいた文字列の検索

文字列のなかに登録された文字は存在するか？

PMA の構築

パターンが複数の場合のパターンマッチング

PMA の構築の高速化

鳩でも分かるC#管理人からのお願い

コメントについて

管理人のモチベーションアップのために

コメントをどうぞ