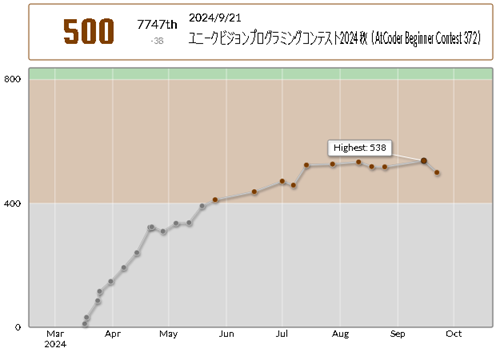
あ~~~やらかしてしまった。ユニークビジョンプログラミングコンテスト2024 秋(AtCoder Beginner Contest 372)で痛恨の大敗北です。なんと1問しか解けませんでした。これまでにない歴史的大敗北です。538 まで上げたレーティングが 500 に激減 (-38)。パフォーマンス 194 もこれまでにない最低値です。とほほ。
ということでヤケ酒を飲みながらひとり反省会です。
B – 3^A
正整数 M が与えられます。 以下の条件を全て満たす正整数 N と非負整数列 A = (A_1, A_2, …, A_N) を一つ求めてください。
1 ≦ N ≦ 20
0 ≦ A_i ≦ 10 (1 ≦ i ≦ N)
3^A_1 + 3^A_2 + … + 3^A_N = Mただし、制約下では条件を満たす N と A の組が必ず存在することが証明できます。
入力されるデータ
M
(ただし1 ≦ M ≦ 100,000)
Mを3進法に変換して3^kの位をCkとすると M = C0 * 3^0 + C1 * 3^1 + … + C10 * 3^10 が成立します。M が 7 だと3進法にすると 21 なので M = 1 * 3^0 + 2 * 3^1となり、Aは0がひとつ、1がふたつある A = (0, 1, 1)が答えとなります。
Mを3進法に変換するには以下のコードでOK。
|
1 2 3 4 5 6 |
List<int> list = new List<int>(); for (int k = 0; k <= 10; k++) // 0 ≦ A_i ≦ 10 (1 ≦ i ≦ N) なので { list.Add(M % 3); M /= 3; } |
この場合は各桁の数だけ A に k を追加すればよいので以下のコードが答えです。また0, 1, 2 だけの11桁であること、M ≦ 100,000 であることから各桁の数字の合計は20以下にしかならず 1 ≦ N ≦ 20 を必ずみたします。
こんな短いコードが書けないとは。ぐぬぬぬ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int M = int.Parse(Console.ReadLine()); List<int> list = new List<int>(); for (int k = 0; k <= 10; k++) { for (int i = 0; i < (M % 3); i++) list.Add(k); M /= 3; } Console.WriteLine(list.Count); Console.WriteLine(string.Join(" ", list)); } } |
C – Count ABC Again
長さ N の文字列 S が与えられます。クエリが Q 個与えられるので、順番に処理してください。
i 番目のクエリは以下の通りです。
整数 X_i と文字 C_i が与えられるので S の X_i 番目の文字を C_i に置き換える。その後 S に文字列 ABC の出現回数を出力する。
入力されるデータ
N Q
S
X_1 C_1
X_2 C_2
:
X_Q C_Qただし
3 ≦ N ≦ 2×10^5
1 ≦ Q ≦ 2×10^5
S は英大文字からなる長さ N の文字列
1 ≦ X_i ≦ N
C_i は英大文字
NとQが最大 2×10^5 なので普通の方法だと制限時間以内にできません。各クエリによって書き換わるのは1文字だけなのでその周辺だけに注目し、差分を考えます。
これは長さ3の文字列である第一引数の先頭からidx番目の文字をcに変更したときの文字列を取得するメソッドです。
|
1 2 3 4 5 6 7 8 9 |
class Program { static string Change(string s, char c, int idx) { char[] vs = s.ToArray(); vs[idx] = c; return new string(vs); } } |
文字列 S のなかにある長さ3 の部分文字列を取得し、”ABC”である個数を数えます。そのあとクエリが飛んできたら対応する部分のみを書き換えます。元の3文字が”ABC”ではなく新しい文字列が”ABC”である場合は個数を増やし、逆の場合は減らします。あとはこれを出力するだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
class Program { static void Main() { int N, Q; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; Q = vs[1]; } string S = Console.ReadLine(); char[] cs = S.ToArray(); List<string> list = new List<string>(); for (int i = 0; i + 2 < S.Length; i++) { char[] arr = new char[] { cs[i], cs[i + 1], cs[i + 2] }; list.Add(new string(arr)); } int count = 0; foreach (string s in list) { if(s == "ABC") count++; } List<int> rets = new List<int>(); for (int i = 0; i < Q; i++) { string[] vs = Console.ReadLine().Split(); int x = int.Parse(vs[0]) - 1; char c = vs[1][0]; if (x >= 2 && x <= N - 1) { string oldString = list[x - 2]; string newString = GetChangeString(list[x - 2], c, 2); if (oldString == "ABC" && newString != "ABC") count--; if (oldString != "ABC" && newString == "ABC") count++; list[x - 2] = newString; } if (x >= 1 && x <= N - 2) { string oldString = list[x - 1]; string newString = GetChangeString(list[x - 1], c, 1); if (oldString == "ABC" && newString != "ABC") count--; if (oldString != "ABC" && newString == "ABC") count++; list[x - 1] = newString; } if (x >= 0 && x <= N - 3) { string oldString = list[x]; string newString = GetChangeString(list[x], c, 0); if (oldString == "ABC" && newString != "ABC") count--; if (oldString != "ABC" && newString == "ABC") count++; list[x] = newString; } rets.Add(count); } foreach(int ret in rets) Console.WriteLine(ret); } } |
D – Buildings
ビル 1, ビル 2, …, ビル N の N 棟のビルがこの順で一列に並んでいます。ビル i (1 ≦ i ≦ N) の高さは H_i です。
各 i = 1, 2, …, N について、次を満たす整数 j (i < j ≦ N) の個数を求めてください。
ビル i とビル j の間にビル j より高いビルが存在しない。
入力されるデータ
N
H_1 H_2 … H_Nただし 1 ≦ N ≦ 2×10^5
1 ≦ H_i ≦ N, i ≠ j なら H_i ≠ H_j
各 i に対して条件を満たす j を昇順に並べた列を J とすると H_J0 H_J1 … は単調増加となります。また J は i + 1 を必ず含みます。この問題は i + 1 項目を起点とする単調増加数列の大きさを問う問題です。
そしてこの問題は後ろから考えたほうがよいです。末項の場合、i + 1 項目が存在しないのでこの場合は0。そのひとつ前の場合は末項のみが存在するので1です。
単調増加数列をスタックにして空のときと最後に追加したものより小さな値のときは追加します。そうでないときは最後に追加したを調べて追加しようとしている値よりも小さな値はすべてPopしてから追加します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; } int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); // 後ろから調べるのでReverse。そのまえに最初の値はいらないのでskipしている A = A.Skip(1).Reverse().ToArray(); List<int> rets = new List<int>(); Stack<int> stack = new Stack<int>(); rets.Add(stack.Count); foreach (int v in A) { Push(stack, v); rets.Add(stack.Count); } // 後ろから調べた値なのでReverseする rets.Reverse(); Console.WriteLine(string.Join(" ", rets)); } static void Push(Stack<int> stack, int v) { if (stack.Count == 0 || stack.Peek() > v) stack.Push(v); else { stack.Pop(); Push(stack, v); } } } |
E – K-th Largest Connected Components
E – K-th Largest Connected Components
N 頂点 0 辺の無向グラフがあります。頂点には 1 から N の番号がつけられています。
Q 個のクエリが与えられるので、与えられた順に処理してください。各クエリは以下の 2 種類のいずれかです。
タイプ 1 : 1 u v の形式で与えられる。頂点 u と頂点 v の間に辺を追加する。
タイプ 2 : 2 v k の形式で与えられる。頂点 v と連結な頂点の中で、k 番目に頂点番号が大きいものを出力する。ただし、頂点 v と連結な頂点が k 個未満のときは -1 を出力する。入力されるデータ
N Q
query 1
query 2
:
query Qただし
1 ≦ N, Q ≦ 2×10^5
1 ≦ k ≦ 10
辺を追加して動的に連結成分を求めるというのであればUnionFind木を使うのかな? ただk 番目に頂点番号が大きいものをどうやって探せばいいかわからずKO。
K の最大値は 10 なので各連結成分ごとにその連結成分に含まれる頂点のうち頂点番号が大きい上位 K 個をリストにして持たせておきます。最初は辺は存在しないのでその連結成分に含まれる頂点は自分自身だけです。
辺が追加されたらUnionFindTree.Uniteメソッド(自作)を実行するのですが、これと同時にリストをマージしソートします。リストの要素の数は最大で 10 なのでこれはそんなに難しくはありません。あとはクエリ 2 が飛んで来たらk 番目に大きい頂点番号を取得して出力するだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 |
using System; using System.Collections.Generic; using System.Linq; class UnionFindTree { int N = 0; int[] Roots = { }; // 頂点番号 x の根 List<int>[] Members = { }; // 頂点番号 x と同じグループの頂点番号上位 K 個 public UnionFindTree(int n) { N = n; Roots = new int[n]; Members = new List<int>[n]; for (int i = 0; i < n; i++) { Roots[i] = i; Members[i] = new List<int>(); Members[i].Add(i); } } public int GetRoot(int x) { if (Roots[x] == x) return x; Roots[x] = GetRoot(Roots[x]); return Roots[x]; } public void Unite(int x, int y) { int rx = GetRoot(x); //xの根 int ry = GetRoot(y); //yの根 if (rx != ry) { Roots[rx] = ry; // xの根とyの根をつなぐ // 頂点番号 x, y と同じグループの頂点番号上位 K 個をマージ・ソートする List<int> list = new List<int>(); list.AddRange(Members[rx]); list.AddRange(Members[ry]); list = list.OrderByDescending(_ => _).ToList(); if (list.Count > 10) list = list.Take(10).ToList(); Members[rx] = list; Members[ry] = list; } } public int Query(int x, int k) { int rx = GetRoot(x); //xの根 if (Members[rx].Count >= k) return Members[rx][k - 1] + 1; else return -1; } } class Program { static void Main() { int N, Q; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; Q = vs[1]; } UnionFindTree uft = new UnionFindTree(N); List<int> rets = new List<int>(); for (int i = 0; i < Q; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int t = vs[0]; if (t == 1) { int a = vs[1] - 1; int b = vs[2] - 1; uft.Unite(a, b); } if (t == 2) { int a = vs[1] - 1; int k = vs[2]; rets.Add(uft.Query(a, k)); } } foreach(int i in rets) Console.WriteLine(i); } } |
