ソートのアルゴリズムの一つにバケットソート(bucket sort)があります。
バケットソート(bucket sort)とは?
バケットとはバケツのことです。このソートアルゴリズムはどんな場合でも使えるわけではありませんが、データの取りうる種類数が限定されている場合は強力な手法となります。
データの取りうる種類数が m 種類であることがわかっているなら、まず m 個のバケツを用意し、値ごとに1個のバケツを対応づけます。次に元のデータ列を走査して、各データを対応するバケツに入れていきます。最後に、整列したい順序に従ってバケツから値を取り出すことで、データをソートすることができます。
データ数が N 個でバケツの数が K 個のとき、計算量はO(N + K)です。これは普通のソートの計算量であるO(NlogN)と比較すると高速であるといえます。
ただしデータの取りうる種類数が多すぎるとバケツを用意することができなくなるので、データの取りうる値が実数全体であったり、整数であっても最大値と最小値の差が大きすぎるなどの理由でその種類数が多い場合は使えないので万能の方法ではありません。
バケットソートの例を示します。以下のコードは実際にバケツを用意するのではなく、各データの個数を数えることで、ソート後のデータの位置を算出してメモリーの消費量を抑えています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
static int[] Bucketsort(int[] src) { int len = src.Length; int[] dst = new int[len]; int min = int.MaxValue; int max = int.MinValue; for (int i = 0; i < len; i++) { min = Math.Min(min, src[i]); max = Math.Max(max, src[i]); } int range = max - min + 2; //int range = max + 2; // 値ごとの出現回数を数える int[] count = new int[range]; for (int i = 0; i < len; i++) count[src[i] - min]++; // ソート後配列における値ごとの開始位置を求める int[] offset = new int[range]; offset[0] = 0; for (int i = 1; i < range; i++) offset[i] = offset[i - 1] + count[i - 1]; // ソート処理 for (int i = 0; i < len; i++) { int target = src[i]; dst[offset[target - min]] = target; offset[target - min]++; } return dst; } |
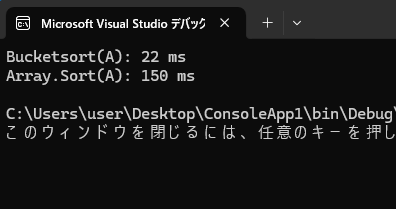
バケットソートは速かった
試しに動作速度を比較してみることにします。ここでは 0 ~ 100,000 – 1 の乱数をつかって長さ1,000,000の配列を生成してソートにかかる時間を計測しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
class Program { static void Main() { Random rand = new Random(); int N = 100 * 10000; int maxValue = 10 * 10000; int[] A = new int[N]; for (int i = 0; i < N; i++) A[i] = rand.Next(maxValue); System.Diagnostics.Stopwatch sw = new System.Diagnostics.Stopwatch(); sw.Reset(); sw.Start(); int[] B = Bucketsort(A); sw.Stop(); Console.WriteLine($"Bucketsort(A): {sw.ElapsedMilliseconds} ms"); sw.Reset(); sw.Start(); Array.Sort(A); sw.Stop(); Console.WriteLine($"Array.Sort(A): {sw.ElapsedMilliseconds} ms"); } } |
差は歴然です。
基数ソートとは?
あとバケットソートを応用したアルゴリズムに基数ソートがあります。
これは最下位桁から最上位桁へ向けてソートする処理を繰り返すと、全体が順序通りに並ぶという手法です。
たとえば 170, 45, 75, 90, 2, 24, 802, 66 をソートする場合を考えます。
まず1の位でソートします。すると、170, 90, 2, 802, 24, 45, 75, 66 となります。次に10の位でソートします。すると 2, 24, 45, 66, 170, 75, 802, 90 のようになります。このとき、ソートは安定ソートでなければなりません。
次に100の位でソートすると 2, 24, 45, 66, 75, 90, 170, 802 となります。1000の位以上はすべて0なのでこれ以上処理を続けても順番は変わりません。そして結果を見てみるとたしかにソートされています。
実際にこの方法で実装して実験してみたのですが、各桁の数を取得するのに時間がかかるらしくあまりいい結果にはなりませんでした。そこで10進法ではなく256進法で考えてみることにします。これだとビット演算で各桁の値を計算するので処理が軽くなります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
static long[] RadixSort(long[] src) { // 負数と非負数はわけて考える long[] plus = src.Where(_ => _ >= 0).ToArray(); long[] minus = src.Where(_ => _ < 0).Select(_ => Math.Abs(_)).ToArray(); int blockSize = 8; int bucketsCount = 1 << blockSize; // 64bit整数なので8bitずつなら8回やればOK for (int i = 0; i < 8; i++) plus = Bucketsort(plus, i); for (int i = 0; i < 8; i++) minus = Bucketsort(minus, i); minus = minus.Select(_ => -1 * _).Reverse().ToArray(); long[] dist = new long[src.Length]; for (int i = 0; i < minus.Length; i++) dist[i] = minus[i]; for (int i = 0; i < plus.Length; i++) dist[i + minus.Length] = plus[i]; return dist; // 256進数の下位idx桁目の値を取得する int GetValue(long v, int idx) { int a = (int)(v >> (blockSize * idx)); int b = (1 << blockSize) - 1; return a & b; } // 前述のメソッドを少し変更しただけ long[] Bucketsort(long[] src, int idx) { int len = src.Length; long[] dst = new long[len]; int[] count = new int[bucketsCount]; for (int i = 0; i < len; i++) count[GetValue(src[i], idx)]++; int[] offset = new int[bucketsCount]; offset[0] = 0; for (int i = 1; i < bucketsCount; i++) offset[i] = offset[i - 1] + count[i - 1]; for (int i = 0; i < len; i++) { long target = src[i]; int num = GetValue(target, idx); dst[offset[num]] = target; offset[num]++; } return dst; } } |
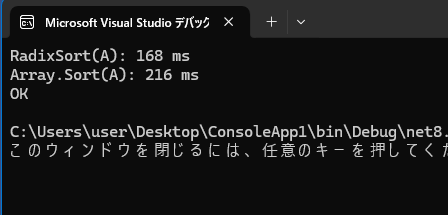
基数ソートもそれなりに速かった
long.MinValue以上long.MaxValue以下の乱数を 1,000,000個生成して普通のソートと実行速度の比較をしてみることにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
class Program { static void Main() { Random rand = new Random(); int N = 100 * 10000; long[] A = new long[N]; for (int i = 0; i < N; i++) { if(rand.Next(2) == 0) A[i] = rand.NextInt64(); else A[i] = -rand.NextInt64(); // ときどき負数も生成する } System.Diagnostics.Stopwatch sw = new System.Diagnostics.Stopwatch(); sw.Reset(); sw.Start(); long[] B = RadixSort(A); sw.Stop(); Console.WriteLine($"RadixSort(A): {sw.ElapsedMilliseconds} ms"); sw.Reset(); sw.Start(); Array.Sort(A); sw.Stop(); Console.WriteLine($"Array.Sort(A): {sw.ElapsedMilliseconds} ms"); // 念のため確認 for (int i = 0; i < A.Length; i++) { if (A[i] != B[i]) { Console.WriteLine("間違っています"); return; } } Console.WriteLine("OK"); } } |
バケットソートを複数回おこなっているのでやや遅くなっていますが、それでもArray.Sortメソッドよりは速いみたいです。