C – Ideal Holidays
C – Ideal Holidaysとは以下のような問題です。
AtCoder 王国の 1 週間は A+B 日からなり、1 日目から A 日目が休日で、A+1 日目から A+B 日目が平日です。
高橋くんは N 個の予定があり、i 番目の予定は今日から D_i 日後です。
高橋くんは今日が 1 週間の何日目かを忘れてしまいました。高橋くんの N 個の予定が全て休日である可能性があるかを判定してください。
入力されるデータ
N A B
D_1 D_2 … D_Nただし
1 ≦ N ≦ 2×10^5
1 ≦ A, B ≦ 10^9
1 ≦ D_1 < D_2 < … < D_N ≦ 10^9
途中まで合っているが間違った解法
D_iが一週間の何日目かが問題なのでA+Bの剰余をとって考えます。そして N = 3, A = 2, B = 5, D = {1, 2, 9} の場合、これを数直線上に表すと以下のようになります。
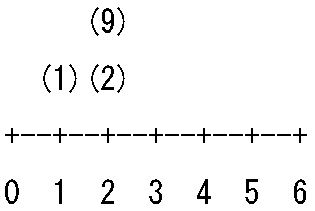
全体をスライドさせてすべてを半開区間 [0, A)にいれることができるなら”Yes”そうでないなら”No”ではないかと考え以下のようなコードを書きました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
// 間違ったコード using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N, A, B; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; A = vs[1]; B = vs[2]; } int[] D = Console.ReadLine().Split().Select(_ => int.Parse(_) % (A + B)).ToArray(); int min = D.Min(); // 全体をminだけ左にスライドさせてすべてがA未満になれば"Yes"でよいのではないか? D = D.Select(_ => _ - min).ToArray(); if (D.All(_ => _ < A)) Console.WriteLine("Yes"); else Console.WriteLine("No"); } } |
結果は不正解。 全部で51あるテストケースのうちひとつだけ通りませんでした。ひとつでも通らなければバグがあるので配点は0です。
全体を左にスライドさせてすべてがA未満になれば”Yes”という考え方はいいとして、どれだけスライドさせるかです。全体の最小値を用いればよいというのが間違っていました。
撃墜ケースと正しい解法
N = 2, A = 5, B = 2, D = {1, 6} の場合、上記コードでは”No”と出力されますが、実際には右に1つスライドさせたり、左に4つスライドさせることで予定をすべて休日にすることができます。つまり正しくは”Yes”です。
一週間の最後の日の次の日は最初の日になるので、円を書いて考えてみます。
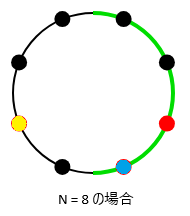
これは N = 3, A = 4, B = 4, D = {3, 4, 6} の場合の図です。赤・青・黄色の丸を等距離移動させることですべての丸を緑の弧の上に乗せることができるかどうかを知りたいのですが、できるとすれば色付きの丸とつぎの色付きの丸の距離がBよりも離れた部分がなければなりません。この場合は黄色から赤までの距離が5(>B)なので”Yes”が答えです。
ということで、正しい解法は以下のとおりです。
これから重複を取り除きソートする(得られた配列をEとする)
E.Length == 1 なら”Yes”である。
それ以外の場合、
E[i+1] – E[i] > B である部分を探す
(E[0] + A + B) – E[last] > B か調べる
どちらかを満たす場合は”Yes”、両方とも満たさない場合は”No”である。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N, A, B; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); N = vs[0]; A = vs[1]; B = vs[2]; } long[] D = Console.ReadLine().Split().Select(_ => long.Parse(_) % (A + B)).ToArray(); D = D.Distinct().OrderBy(_ => _).ToArray(); bool yes = false; // 見落としがちなコーナーケース if(D.Length == 1) yes = true; for (int i = 0; i < D.Length - 1; i++) { if(D[i + 1] - D[i] > B) yes = true; } if (D[0] + A + B - D[D.Length - 1] > B) yes = true; if (yes) Console.WriteLine("Yes"); else Console.WriteLine("No"); } } |
