数独をバックトラック法で解きます。
数独は3×3のグループ(ブロック)に区切られた 9×9の正方形の枠内に1から9までの数字を入れるパズルの一つです。アメリカのパズル誌に載っていた「Number Place」というパズルを、パズル制作会社ニコリが、名称を「数字は独身に限る」(略して、数独)と変えて日本で発表したことからこの名前が一般的になりました。
ルールは以下のとおり。
空いているマスに、1 から 9 のいずれかの数字を入れる。
縦・横の各列に同じ数字が重複して入ってはいけない。
太線で囲まれた3×3の「ブロック」内に同じ数字が重複して入ってはいけない。
Contents
世界で最も難しい数独
世界で最も難しい数独によるとこの問題が世界で最も難しい数独のようです。
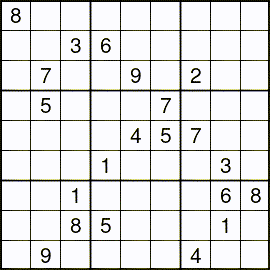
科学と応用数学の博士号を持つフィンランドの環境科学者Arto Inkala氏が作成したもので作成に3ヵ月を要したそうです。さて鳩が作成したプログラムで解くことはできるのでしょうか?
あれ?簡単にできてしまったのだが?
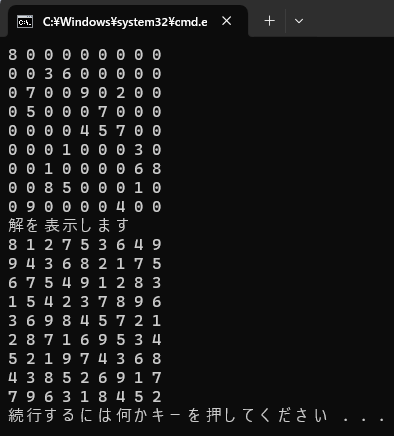
上の9行が問題になっていて 0 の部分が空いているマスです。そして下の9行が得られた解です。
数独をバックトラック法で解く
ではどのようなコードを書いたのかを解説します。
後述する NumberPlaceクラスに二次元配列を渡して解を求めています。そのあと得られた解がほんとうに数独の条件を満たしているのか念の為確認し、表示させています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
class Program { static void Main() { int[,] map = new int[9, 9]; for (int row = 0; row < 9; row++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); for (int col = 0; col < 9; col++) map[row, col] = vs[col]; } NumberPlace numberPlace = new NumberPlace(map); int[,] rets = numberPlace.Solve(map); if (numberPlace.Check(rets)) { Console.WriteLine("解を表示します"); for (int row = 0; row < 9; row++) { int[] vs = new int[9]; for (int col = 0; col < 9; col++) vs[col] = rets[row, col]; Console.WriteLine(string.Join(" ", vs)); } } else Console.WriteLine("NG"); } } |
NumberPlaceクラスを定義する
NumberPlaceクラスのフィールド変数をしめします。
縦・横の各列に同じ数字が重複して入ってはならないので、各行と列のマスに入っている値をHashSetに格納します。行と列はそれぞれ9つあるのでHashSetの配列を定義します。同様に3×3のブロック内に同じ数字が重複して入ってはならないので、これもHashSetの配列で管理します。これで各マスにいれることができる値を高速に取得することができます。
IsFixedは問題として与えられたすでに確定しているマスかどうかを示すものです。Values はマスに入る値です。未確定の場合は 0 です。このすべての要素に 0 以外の値を格納することができれば問題を解くことができたことになります。
CurRowとCurColは現在どの値が入るかを調べている部分です。
|
1 2 3 4 5 6 7 8 9 10 11 |
class NumberPlace { HashSet<int>[] RowSets = new HashSet<int>[9]; HashSet<int>[] ColSets = new HashSet<int>[9]; HashSet<int>[,] BlockSets = new HashSet<int>[3, 3]; bool[,] IsFixed = new bool[9, 9]; int[,] Values = new int[9, 9]; int CurRow = 0; int CurCol = 0; } |
コンストラクタ
コンストラクタを示します。
HashSetの配列を初期化し、引数として与えられた二次元配列の値を各フィールド変数に格納していきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
class NumberPlace { public NumberPlace(int[,] values) { for (int i = 0; i < 9; i++) RowSets[i] = new HashSet<int>(); for (int i = 0; i < 9; i++) ColSets[i] = new HashSet<int>(); for (int i = 0; i < 9; i++) BlockSets[i / 3, i % 3] = new HashSet<int>(); for (int row = 0; row < 9; row++) { for (int col = 0; col < 9; col++) { int v = values[row, col]; if (v != 0) { IsFixed[row, col] = true; RowSets[row].Add(v); ColSets[col].Add(v); BlockSets[row / 3, col / 3].Add(v); } } } Values = (int[,])values.Clone(); } } |
マスに値をいれることができるか?
マスに値をいれることができるかを調べる処理を示します。
縦・横の各列、3×3のブロック内に同じ数字が重複して入ってはならないので、マスに対応するHashSetにその値が格納されていないことを確認しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class NumberPlace { bool CanSet(int row, int col, int value) { if (RowSets[row].Contains(value)) return false; if (ColSets[col].Contains(value)) return false; if (BlockSets[row / 3, col / 3].Contains(value)) return false; return true; } } |
マスに値をいれる処理と削除する処理
マスに値をいれる処理と削除する処理を示します。
マスに値をいれるときは前に入っていた値に関する情報を削除しなければなりません。マスに値をいれるときはHashSetに値をAddし、Valuesを書き換えます。また削除するときはHashSetから値をRemoveし、Valuesを 0 に書き換えます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
class NumberPlace { void SetValue(int row, int col, int value) { RemoveValue(row, col); RowSets[row].Add(value); ColSets[col].Add(value); BlockSets[row / 3, col / 3].Add(value); Values[row, col] = value; } void RemoveValue(int row, int col) { int value = Values[row, col]; RowSets[row].Remove(value); ColSets[col].Remove(value); BlockSets[row / 3, col / 3].Remove(value); Values[row, col] = 0; } } |
現在位置の前進と後退
CurRowとCurColを前に進める処理と後退させる処理を示します。
前に進めるときはCurColをインクリメントします。もし 9 になってしまった場合は 0 に戻し、CurRowをインクリメントします。また確定した値が入っている部分とIsFixedがtrueの部分はスキップして前にすすめます。
後退させるときはCurColをデクリメントします。もし -1 になってしまった場合は 8 に戻し、CurRowをデンクリメントします。また値が確定していない部分とIsFixedがtrueの部分はスキップして後退させます。
戻り値がfalseのときはこれ以上、進めない、戻れない場合です。前のマスの値が確定して次に進もうとしたらこれ以上進めない場合とはすべてのマスの値が確定したときです。またマスの値を消去して前に戻ろうとしたらこれ以上戻れない場合とは解が存在しない場合です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class NumberPlace { bool GoNext() { while (IsFixed[CurRow, CurCol] || Values[CurRow, CurCol] != 0) { CurCol++; if (CurCol == 9) { CurCol = 0; CurRow++; if (CurRow == 9) return false; } } return true; } bool GoBack() { while (IsFixed[CurRow, CurCol] || Values[CurRow, CurCol] == 0) { CurCol--; if (CurCol == -1) { CurCol = 8; CurRow--; if (CurRow == -1) return false; } } return true; } } |
数独の条件を満たすかチェックする
念のため作成したメソッドです。渡された二次元配列が数独の条件を満たすかチェックするメソッドです。
ほんとうに数独の条件を満たしているのであれば各行と各列には1から9までの値がすべて漏れなく格納されていなければなりません。これはHashSetに格納されている値の個数が9であるかを調べればわかります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
class NumberPlace { public bool Check(int[,] values) { HashSet<int>[] rowSets = new HashSet<int>[9]; for (int i = 0; i < 9; i++) rowSets[i] = new HashSet<int>(); HashSet<int>[] colSets = new HashSet<int>[9]; for (int i = 0; i < 9; i++) colSets[i] = new HashSet<int>(); HashSet<int>[,] blockSets = new HashSet<int>[3, 3]; for (int i = 0; i < 9; i++) blockSets[i / 3, i % 3] = new HashSet<int>(); for (int row = 0; row < 9; row++) { for (int col = 0; col < 9; col++) { int v = values[row, col]; if (v <= 0 || v >= 10) // 不正な値は弾く continue; rowSets[row].Add(v); colSets[col].Add(v); blockSets[row / 3, col / 3].Add(v); } } for (int i = 0; i < 9; i++) { if (rowSets[i].Count != 9) return false; } for (int i = 0; i < 9; i++) { if (colSets[i].Count != 9) return false; } for (int i = 0; i < 9; i++) { if (blockSets[i / 3, i % 3].Count != 9) return false; } return true; } } |
求解メソッド
解を求める処理を示します。
GoNextメソッドで空いているマスまで移動してそのマスに入る値でもっとも小さいものを仮にSetValueメソッドで設定します。そしてGoNextメソッドで別の空いているマスを探して移動します。GoNext() == false なら解が得られたことになるので終了です。
現在調べているマスに入る値が見つからない場合は前のマスに入れた値が間違っていることになります。前のマスに戻って仮に入れている値よりも大きな値でいれることができる値がないか調べます。もし見つからない場合はその値を削除して、さらに前に戻ります。
このような処理をGoNextメソッドかGoBackメソッドがfalseを返すまで繰り返します。終わったら二次元配列 Values を戻り値として返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
class NumberPlace { public int[,] Solve(int[,] map) { CurRow = 0; CurCol = 0; while (true) { if (!GoNext()) break; bool isset = false; // 現在調べているマスに入る値があるか調べる for (int v = 1; v <= 9; v++) { if (CanSet(CurRow, CurCol, v)) { SetValue(CurRow, CurCol, v); isset = true; break; } } // 現在調べているマスに入る値がない場合は前に戻る while (!isset) { RemoveValue(CurRow, CurCol); if (!GoBack()) break; int old = Values[CurRow, CurCol]; for (int v = old + 1; v <= 9; v++) { if (CanSet(CurRow, CurCol, v)) { SetValue(CurRow, CurCol, v); isset = true; break; } } } } return Values; } } |
