Contents
ヒストグラム中の最大の長方形の面積は?
緑色の部分から最大の長方形を探す問題です。
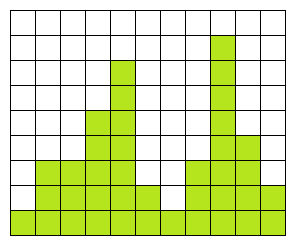
これは最大長方形問題を解く 面積が最大の長方形を見つけるアルゴリズムでもやったように、スタックを利用してO(N)で解を求める方法があります。
Rectクラスの定義と基本方針
|
1 2 3 4 5 6 7 8 9 10 |
public class Rect { public Rect(int left, int height) { Left = left; Height = height; } public int Left = 0; public int Height = 0; } |
ヒストグラムの各長方形の左側の位置と高さでオブジェクトを生成してスタックに入れていくわけですが、そのときに以下の処理をおこないます。
スタックが空の場合やスタックの頂点にある長方形の高さがrectの高さより低い場合はスタックに rect を push します。スタックの頂点にある長方形の高さが rect の高さと等しい場合は何もしません。
重要なのはスタックの頂点にある長方形の高さがrectの高さより高い場合の処理です。
この場合はスタックが空でなく、スタックの頂点にある長方形の高さが rect の高さより高い場合は、スタックから長方形を pop します。そしてその面積を計算します。これは pop されたオブジェクトの Height と現在の位置 i とオブジェクトの Left から計算できます。
そのあとスタックに rect を push するのですが、このときに Left は最後にスタックから取り出した長方形の Left の値とします。ただし、このときにスタックの頂点にある長方形の高さが push しようとしているオブジェクトの高さと同じ場合はPushはしないでそのままにします。
最大長方形問題を解く 面積が最大の長方形を見つけるアルゴリズムの説明と少し違いますが、この方法のほうが最大長方形の面積を求めるだけでなくヒストグラムのなかにある長方形の個数を求めることもできるので汎用性があると思います。
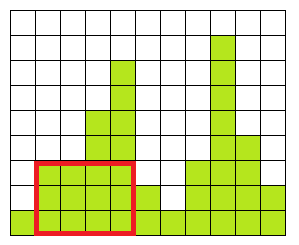
冒頭の図だと以下のような処理がおこなわれます。
(Left: 0, Height:1), (Left: 1, Height:3), (Left: 3, Height:5), (Left: 4, Height:7)をPushする(Left: 2は前のものとHeightが同じなのでとばす)。
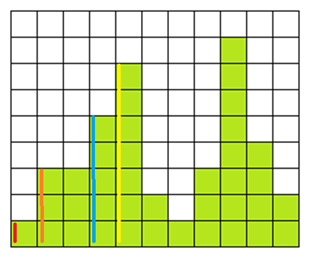
(Left: 5, Height:2) はスタックの頂上よりも Height が小さいのでそのまま push してはならない。Height が 2 より大きな (Left: 4, Height:7), (Left: 3, Height:5), (Left: 1, Height:3) を pop して(高さ = 7, 幅 = 5 – 4 = 1), (高さ = 5, 幅 = 5 – 3 = 2), (高さ = 3, 幅 = 5 – 1 = 4)の長方形を確定する。
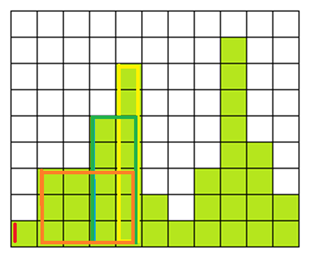
最後に pop したのが (Left: 1, Height:3) なので (Left: 5, Height:2) の Leftを 1 に変更して push する。
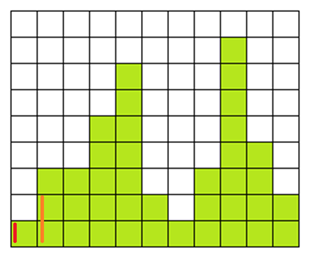
(Left: 6, Height:1) はスタックの頂上よりも Height が小さいので Height が 1 より大きいものを pop する。これによって (Left: 5, Height:2) が pop され、(幅 = 5、高さ = 2)の長方形が確定する。
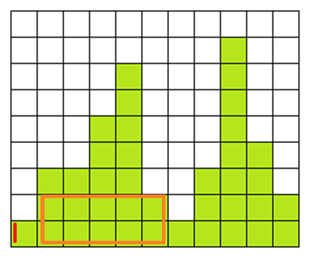
スタックの頂点にある長方形の高さが Push しようとしているオブジェクトの高さと同じ 1 なのでここでは push はしない。
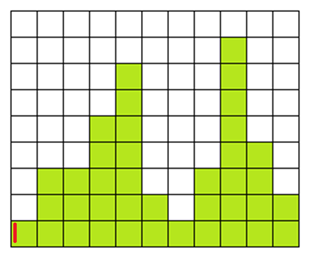
(Left: 7, Height:3), (Left: 8, Height:8) をpushする。
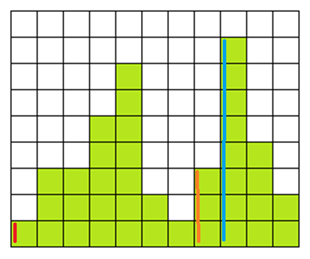
(Left: 9, Height:4) はスタックの頂上よりも Height が小さいので Height が 4 より大きいものを pop する。これによって(Left: 8, Height:8)が pop され、(幅 = 1, 高さ = 8)の長方形が確定する。
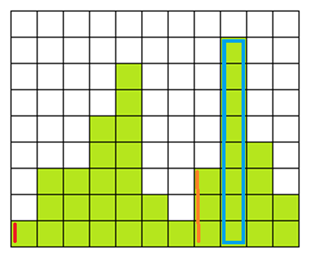
最後に pop したのが (Left: 8, Height:8) なので (Left: 9, Height:4) の Left を 8 に変更して push する。
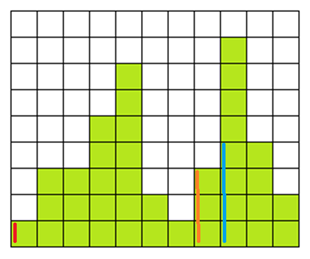
(Left: 10, Height:2)はスタックの頂上よりも Height が小さいので Height が 2 より大きいものを pop する。これによって(Left: 8, Height:4), (Left: 7, Height:3)が pop され、(幅 = 2, 高さ = 4)(幅 = 3, 高さ = 3)の長方形が確定する。
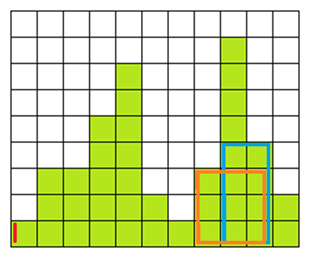
最後に pop したのが(Left: 7, Height:3)なので (Left: 10, Height:2) を (Left: 7, Height:2) に変更してpushする。
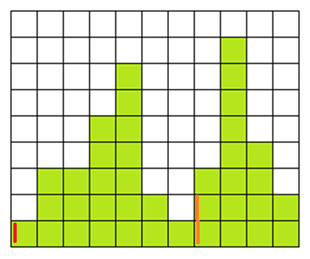
終了したのでスタックのなかにある (Left: 7, Height:2), (Left: 0, Height:1)をpopする。これによって(幅 = 4, 高さ = 4)(幅 = 11, 高さ = 1)の長方形が確定する。
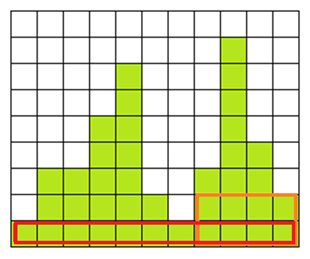
確定した長方形のなかでもっとも面積が大きなものが求めようとしている長方形である。
Histogramクラスの定義
上記のような処理をするクラスを定義します。
Solveを呼び出すとヒストグラムのなかにある長方形の数と長方形の面積の最大値を取得することができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
class Histogram { public class Rect { public Rect(int left, long height) { Left = left; Height = height; } public int Left = 0; public long Height = 0; } int[] Values = new int[1]; long MaxValue = long.MinValue; int RectsCount = 0; public Histogram(int[] values) { Values = (int[])values.Clone(); } public long GetMaxValue() { if (MaxValue == long.MinValue) Solve(); return MaxValue; } public long GetRectsCount() { if (RectsCount == 0) Solve(); return RectsCount; } public void Solve() { List<long> A = new List<long>(); foreach (int i in Values) A.Add(i); // 最後に 0 を付加するとループを抜けたときスタックは空になっているので // ループを抜けたあとの処理を省略することができる A.Add(0); long max = 0; int count = 0; Stack<Rect> stack = new Stack<Rect>(); for (int i = 0; i < A.Count; i++) { if (stack.Count == 0) stack.Push(new Rect(i, A[i])); else { long height = stack.Peek().Height; if (height < A[i]) stack.Push(new Rect(i, A[i])); else if (height > A[i]) { Rect lastPop = null; while (stack.Count > 0 && A[i] < stack.Peek().Height) { Rect rect = stack.Pop(); long area = (i - rect.Left) * rect.Height; lastPop = rect; max = Math.Max(max, area); count++; } if (lastPop != null && (stack.Count == 0 || stack.Peek().Height != A[i])) stack.Push(new Rect(lastPop.Left, A[i])); } } } MaxValue = max; RectsCount = count; } } |
D – カーペット
部屋にカーペットを敷くことになった。この問題では部屋を上から見たときの床を二次元平面上の多角形とみなす。床の形状を表す要素数 N の数列 A_1, A_2, …, A_N が与えられる。
R_i を左下の座標が(i, 0)で右上の座標が(i + 1, a_i)である各辺が x 軸または y 軸に平行な長方形の境界及び内部領域とする。このとき,床を表す多角形はR_1 ∪ R_2 ∪ R_3 ∪ … ∪ R_N によって表される。カーペットは長方形であればどんな大きさのものを何枚でも用意することができる。以下の条件を満たすようにカーペットを配置し部屋の床を全て覆いつくしたい。
カーペットは研究室からはみ出してはいけない。
カーペットはいくらでも重ねて敷くことが可能である。このときカーペットの厚さは無視する。
カーペットを切り離して利用することはできない。
カーペットは各辺がx軸またはy軸に平行になるように配置しなければならない。
研究室の床を覆い尽くすために必要なカーペットの最小数を求めよ。入力されるデータ
N
A_1 A_2 … A_N
(ただし、1 ≦ N ≦ 2×10^5, 1 ≦ a_i ≦ 10^9 )
これはヒストグラムのなかの長方形の数を数えよという問題と同じです。上で定義したHistogram クラスを使って解を求めることができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
using System; using System.Collections.Generic; using System.Linq; // Histogram クラスは同じなので省略 class Program { static void Main() { int N = int.Parse(Console.ReadLine()); int[] A = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); Histogram histogram = new Histogram(A); Console.WriteLine(histogram.GetRectsCount()); } } |
最大長方形問題を解く

ヒストグラム中の最大長方形問題を解くときのアルゴリズムを用いて最大長方形問題を解くことができます。まず各要素について上に向かってtrueが何個連続しているかを示す配列のリストを作ります。次にリストに格納されている配列をヒストグラムの入力と見なしヒストグラムの最大長方形の面積を求める処理をおこないます。

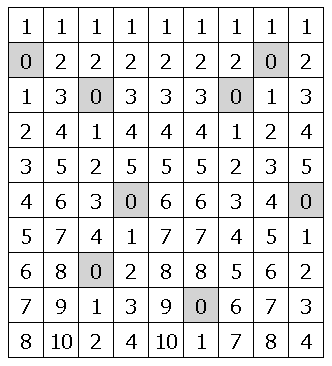
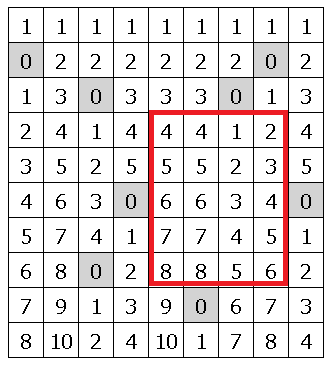
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
class MaxRectangle { int H, W; bool[,] Map = new bool[1, 1]; public MaxRectangle(bool[,] map) { Map = (bool[,])map.Clone(); H = map.GetLength(0); W = map.GetLength(1); } public long Solve() { List<int[]> arrays = new List<int[]>(); for (int row = 0; row < H; row++) arrays.Add(new int[W + 1]); for (int row = 0; row < H; row++) { for (int col = 0; col < W; col++) { if (row == 0) arrays[0][col] = Map[0, col] ? 1 : 0; else arrays[row][col] = Map[row, col] ? arrays[row - 1][col] + 1 : 0; } } long max = 0; foreach (var arr in arrays) { Histogram histogram = new Histogram(arr); max = Math.Max(max, histogram.GetMaxValue()); } return max; } } class Program { static void Main() { string[] map = { ".........", "#......#.", "..#...#..", ".........", ".........", "...#....#", ".........", "..#......", ".....#...", }; int H = map.Length; int W = map[0].Length; bool[,] map2 = new bool[H, W]; for(int row = 0; row < H; row++) { char[] vs = map[row].ToArray(); for (int col = 0; col < W; col++) map2[row, col] = vs[col] == '.'; } MaxRectangle maxRectangle = new MaxRectangle(map2); Console.WriteLine(maxRectangle.Solve()); } } |
F – Flip and Rectangles
H × W のマス目があります。マス目の各マスは黒か白かに塗られており、上から i 番目、左から j 番目のマスは S_i の j 文字目が # のとき黒マスで . のとき白マスです。
マス目に対して次の操作を好きな回数行うことができます。
マス目の任意の行または列を選び、その行または列のすべてのマスの色を反転する (すなわち黒で塗られたマスを白に、白で塗られたマスを黒に塗り替える)。
操作の後、マス目に沿った長方形を 1 個選びます。このとき選んだ長方形に含まれるすべてのマスは黒で塗られていなければなりません。うまく操作を行うとき選ぶことができる最大の長方形の面積を求めてください。
入力されるデータ
H W
S 1
S 2
:
S H
(ただし、2 ≦ H ≦ 2000, 2 ≦ W ≦ 2000, S_i =|W|
S_i は #, . のみからなる)
マス目に含まれる 2 × 2 の部分であって、黒マスを奇数個含むものを「悪い部分」と定義します。ある長方形が悪い部分を含む場合、どう操作を行ってもその部分をすべて黒で塗られた状態にすることはできません。
うまく操作を行えばある長方形の内部がすべて黒で塗られた状態になることと、その長方形が悪い部分を含まないことは同値です。
マス目においてすべての悪い部分の中心の格子点に印を付けてみます。すると選ぶことができる長方形は内部に印を含まない長方形になります。これも最大長方形問題に帰着できます。
格子点にある印を含まない最大長方形はどのようにすれば求めることができるでしょうか?
まずマスの右上に印があるマスは 1 にリセットしてそれ以外は上のマスに 1 を加えます。また最後の列は 0 とみなします。
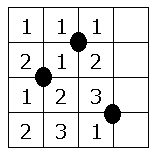
あとは上記とほぼ同じですが、前の例題のケースと比較すると長方形を確定するときに幅がひとつだけ大きくなることに気が付きます。
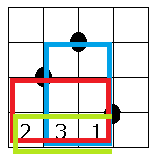
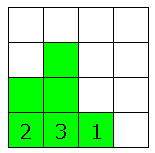
また印の配置に関係なく1行または1列まるごと選択することができます。
そのため以下のようなコードになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 |
class MaxRectangle2 { public class Rect { public Rect(int left, long height) { Left = left; Height = height; } public int Left = 0; public long Height = 0; } int H, W; bool[,] BlotMap = new bool[1, 1]; // セルの右肩に印があれば true public MaxRectangle2(int h, int w, bool[,] map) { H = h; W = w; BlotMap = (bool[,])map.Clone(); } public long Solve() { int[,] map = new int[H, W]; for (int col = 0; col < W; col++) map[0, col] = 1; for (int row = 1; row < H; row++) { for (int col = 0; col < W; col++) { if (BlotMap[row, col]) map[row, col] = 1; else map[row, col] = map[row - 1, col] + 1; } } long ans = Math.Max(H, W); for (int row = 0; row < H; row++) { int[] vs = new int[W]; for (int col = 0; col < W - 1; col++) vs[col] = map[row, col]; vs[W - 1] = 0; ans = Math.Max(ans, SolveHelper(vs)); } return ans; } public long SolveHelper(int[] arr) { List<int> vs = new List<int>(arr); long max = 0; int count = 0; Stack<Rect> stack = new Stack<Rect>(); for (int i = 0; i < vs.Count; i++) { if (stack.Count == 0) stack.Push(new Rect(i, vs[i])); else { long height = stack.Peek().Height; if (height < vs[i]) stack.Push(new Rect(i, vs[i])); else if (height > vs[i]) { Rect lastPop = null; while (stack.Count > 0 && vs[i] < stack.Peek().Height) { Rect rect = stack.Pop(); long area = (i - rect.Left + 1) * rect.Height; lastPop = rect; max = Math.Max(max, area); count++; } if (lastPop != null && (stack.Count == 0 || stack.Peek().Height != vs[i])) stack.Push(new Rect(lastPop.Left, vs[i])); } } } return max; } } class Program { static void Main() { int H, W; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); H = vs[0]; W = vs[1]; } char[,] map = new char[H, W]; for (int row = 0; row < H; row++) { char[] vs = Console.ReadLine().ToArray(); for (int col = 0; col < W; col++) map[row, col] = vs[col]; } // 悪い部分に印をつける bool[,] map2 = new bool[H, W]; for (int row = 1; row < H; row++) { for (int col = 1; col < W; col++) { int count = 0; count += map[row - 1, col - 1] == '#' ? 1 : 0; count += map[row - 1, col] == '#' ? 1 : 0; count += map[row, col - 1] == '#' ? 1 : 0; count += map[row, col] == '#' ? 1 : 0; if (count % 2 == 1) map2[row, col - 1] = true; } } MaxRectangle2 mr = new MaxRectangle2(H, W, map2); Console.WriteLine(mr.Solve()); } } |
