強連結成分分解をして充足可能性問題を解く

Contents

1 充足可能性問題とは？
2 Implication グラフ
3 強連結成分分解をして充足可能性問題を解いてみる
- 3.1 H – Two SAT
  - 3.1.1 実装してみる
4 TwoSAT クラスを定義する
5 TwoSAT クラスを用いて問題を解いてみる
- 5.1 No.274 The Wall

充足可能性問題とは？

充足可能性問題（satisfiability problem, SAT）は、一つの命題論理式が与えられたとき、それに含まれる変数の値を偽 (False) あるいは真 (True) にうまく定めることによって全体の値を真にできるか、という問題です。

真偽値をとる論理変数 x1, x2, x3, x4 … および論理演算子により論理式が構成されます。

◯論理否定 (￢x1)
　x1 が真ならば偽偽ならば真
◯論理和 (x1 ∨ x2)
　x1 が真ならば x1、偽ならば x2
◯論理積 (x1 ∧ x2)
　x1 が真ならば x2、偽ならば x1
◯リテラル
　論理変数 (x1) またはその否定 (￢x1)
◯節
　リテラルの論理和 (x1 ∨ x2)

論理式全体の値を真にするような、真偽値 x1, x2, x3, x4 … の組み合わせは存在するかを問う充足可能性問題はNP完全ですが、論理積でつながれたひとつひとつの部分(節)に変数が二つしかない 2-SAT問題は節の数と変数の数に対する線形時間のアルゴリズムが存在します。節の長さが 3 以上の場合はNP完全に属します。

Implication グラフ

Implicationとは「包含」という意味であり、論理で言えば論理包含がこれにあたります。命題P, Qに対しての論理包含を P ⇒ Q 等と書き、「P が偽または Q が真」という意味を表します。

(P ⇒ Q) ⇔ (￢P ∨ Q)
(￢P ⇒ Q) ⇔ (P ∨ Q)
(￢P ⇒ Q) ⇔ (P ∨ Q) ⇔ (Q ∨ P) ⇔ (￢Q ⇒ P)
(P ∨ Q) ⇔ (￢P ⇒ Q) ∧ (￢Q ⇒ P)

入力の論理式の論理和を論理包含によって書きなおすことができます。このグラフの頂点集合は変数とその否定であり、辺は論理包含の関係を表します。このグラフでは u ⇒ v の場合にだけ頂点 u, v 間に有向辺が存在します。

このグラフの強連結成分について考えてみましょう。強連結成分であるということはその集合内の任意の2頂点間に有向道が存在するということです。

x から y への有向道が存在するということは強連結成分の定義から y から x への有向道も存在することを意味します。 x ⇒ y なら y ⇒ x ということになります。

もし x と y がある変数の真偽値とその否定の真偽値であった場合、どうなるでしょうか？これは変数の真偽値の関係に矛盾が生じているということを意味します。

Implication グラフを強連結成分分解した結果、ある変数とその否定が同じ強連結成分に属していた場合、与えられた論理式は充足できないということになります。これによって充足可能性問題を解くことができます。

強連結成分分解をして充足可能性問題を解いてみる

H – Two SAT

1 から N までの番号のついた N 本の旗があります。これらの旗を数直線状に設置します。

旗 i は座標 X_i または座標 Y_i に設置することができます。ただしどの 2 つの旗についても，その間の距離が D 以上である必要があります。

N 本の旗を設置することが可能かどうか判定し、可能であるならば実際に置き方を 1 つ示してください。

入力されたデータ
N D
X_1 Y_1
X_2 Y_2
…
X_N Y_N
（ただし、1 ≦ N ≦ 1000, 0 ≦ D ≦ 10^9
0 ≦ X i ＜ Y i ≦ 10^9 ）

各旗は「座標 X_i に設置する」「座標 X_i に設置しない (Yi に設置する)」という 2 通りずつの選択肢があります。そこで x_i を旗iを「座標 X_i に設置するかどうか？」と定義します。

すると旗 a とそれ以外の旗 b の関係から x_a は以下のようになります。

もし以下のような入力が与えられた場合、どうなるかを考えてみます。

旗 0 は 1 4
旗 1 は 2 5
旗 2 は 0 6
2 以上離すこと

|X_0 – X_1| ＜ 2 なので x_0 == false ∨ x_1 == false
|Y_0 – Y_1| ＜ 2 なので x_0 == true ∨ x_1 == true
|X_0 – X_2| ＜ 2 なので x_0 == false ∨ x_2 == false
|Y_1 – Y_2| ＜ 2 なので x_1 == true ∨ x_2 == true

(P ∨ Q) ⇔ (￢P ⇒ Q) ∧ (￢Q ⇒ P) だったので ⇒ を用いて表現すると以下のようになります。

x_0 == false ∨ x_1 == false なので x_0 ⇒ ￢x_1, x_1 ⇒ ￢x_0
x_0 == true ∨ x_1 == true なので￢x_0 ⇒ x_1, ￢x_1 ⇒ x_0
x_0 == false ∨ x_2 == false なので x_0 ⇒ ￢x_2, x_2 ⇒ ￢x_0
x_1 == true ∨ x_2 == true なので￢x_1 ⇒ x_2, ￢x_2 ⇒ x_1

xi と￢xi の頂点を生成して ⇒ で辺を張り、強連結成分分解をしたときに、同じ強連結成分のなかに xi と￢xi が存在しなければ旗を設置することが可能ということになります。

ところで同じ強連結成分のなかに x_i と￢x_i が存在しない場合、x_i は true か false のどちらなのかを確定させることができるのですが、どのようにして確定させればよいのでしょうか？

強連結成分分解は深さ優先探索をして各頂点に通し番号の ID をつけ、辺を逆にして大きいものから再度深さ優先探索をするという処理をおこないます。このとき先に確定した強連結成分に番号をつけていきます。x_i に相当する頂点の番号のほうが￢x_i に相当する頂点の番号よりも大きい場合 xi は true です。

実装してみる

Vertex クラス、Dfs1 メソッド、Dfs2 メソッドは強連結成分分解蟻本読書会と同じなので省略しています。

x_i に対応する頂点とこの論理否定に該当する頂点が必要なので全部で N * 2 個の頂点が必要です。ここでは x_i に対応する頂点の頂点番号を i とし、この論理否定に該当する頂点番号を i + N とします。

Implication グラフを生成することができたらあとは強連結成分分解をして求解するだけです。

using System;
using System.Collections.Generic;
using System.Linq;

public class Program
{
    static int nextId = 0;
    static Vertex[] vertices = { };
    static bool[] visits = { };

    static void Main()
    {
        int N, D;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            D = vs[1];
        }

        int[] X = new int[N];
        int[] Y = new int[N];
        for (int i = 0; i < N; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            X[i] = vs[0];
            Y[i] = vs[1];
        }

        // 連結リストと逆向きの連結リストを生成する
        List<int>[] list = new List<int>[N * 2];
        List<int>[] rlist = new List<int>[N * 2];

        for (int i = 0; i < N * 2; i++)
        {
            list[i] = new List<int>();
            rlist[i] = new List<int>();
        }

        // 論理否定に該当する頂点番号を返す
        int take_not(int x)
        {
            if (x < N)
                return x + N;
            else
                return x - N;
        }

        // 連結リストと逆向きの連結リストに辺を追加する
        void addEdge(bool xTrue, int x, bool yTrue, int y)
        {
            if (!xTrue)
                x = take_not(x);
            if (!yTrue)
                y = take_not(y);

            list[take_not(x)].Add(y);
            list[take_not(y)].Add(x);

            rlist[y].Add(take_not(x));
            rlist[x].Add(take_not(y));
        }

        for (int a = 0; a < N; a++)
        {
            for (int b = a + 1; b < N; b++)
            {
                if (Math.Abs(X[a] - X[b]) < D)
                    addEdge(false, a, false, b);
                if (Math.Abs(X[a] - Y[b]) < D)
                    addEdge(false, a, true, b);
                if (Math.Abs(Y[a] - X[b]) < D)
                    addEdge(true, a, false, b);
                if (Math.Abs(Y[a] - Y[b]) < D)
                    addEdge(true, a, true, b);
            }
        }

        // 連結リストに辺を追加したので強連結成分分解の処理をおこなう（やることは前回と同じ）
        visits = new bool[N * 2];
        vertices = new Vertex[N * 2];

        for (int i = 0; i < N * 2; i++)
            Dfs1(i, list);

        vertices = vertices.OrderByDescending(_ => _.ID).ToArray();

        // 頂点番号からどの強連結成分に属するのか辞書から取得できるようにする
        // 先に確定した強連結成分から通し番号をつける
        int groupNumber = 0;
        Dictionary<int, int> dic = new Dictionary<int, int>();

        visits = new bool[N * 2];
        foreach (Vertex vertex in vertices)
        {
            List<int> ret = Dfs2(vertex.Number, rlist);
            foreach (int i in ret)
                dic.Add(i, groupNumber);

            groupNumber++;
        }

        bool bad = false;
        List<long> values = new List<long>();
        for (int i = 0; i < N; i++)
        {
            // 同じ強連結成分内に xi と ￢xi に相当する頂点がある場合は論理式は充足できない
            if (dic[i] == dic[take_not(i)])
            {
                bad = true;
                break;
            }
            // 異なる強連結成分内に xi と ￢xi が存在する場合は
            // xi が true なのか false なのかを確定する
            if (dic[i] > dic[take_not(i)])
                values.Add(X[i]);
            else
                values.Add(Y[i]);
        }

        if (bad)
            Console.WriteLine("No");
        else
        {
            Console.WriteLine("Yes");
            foreach(int v in values)
                Console.WriteLine(v);
        }
    }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

using System;

using System.Collections.Generic;

using System.Linq;

public class Program

{

static int nextId = 0;

static Vertex[] vertices = { };

static bool[] visits = { };

static void Main()

{

int N, D;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

D = vs[1];

}

int[] X = new int[N];

int[] Y = new int[N];

for (int i = 0; i < N; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

X[i] = vs[0];

Y[i] = vs[1];

}

// 連結リストと逆向きの連結リストを生成する

List<int>[] list = new List<int>[N * 2];

List<int>[] rlist = new List<int>[N * 2];

for (int i = 0; i < N * 2; i++)

{

list[i] = new List<int>();

rlist[i] = new List<int>();

}

// 論理否定に該当する頂点番号を返す

int take_not(int x)

{

if (x < N)

return x + N;

else

return x - N;

}

// 連結リストと逆向きの連結リストに辺を追加する

void addEdge(bool xTrue, int x, bool yTrue, int y)

{

if (!xTrue)

x = take_not(x);

if (!yTrue)

y = take_not(y);

list[take_not(x)].Add(y);

list[take_not(y)].Add(x);

rlist[y].Add(take_not(x));

rlist[x].Add(take_not(y));

}

for (int a = 0; a < N; a++)

{

for (int b = a + 1; b < N; b++)

{

if (Math.Abs(X[a] - X[b]) < D)

addEdge(false, a, false, b);

if (Math.Abs(X[a] - Y[b]) < D)

addEdge(false, a, true, b);

if (Math.Abs(Y[a] - X[b]) < D)

addEdge(true, a, false, b);

if (Math.Abs(Y[a] - Y[b]) < D)

addEdge(true, a, true, b);

}

// 連結リストに辺を追加したので強連結成分分解の処理をおこなう（やることは前回と同じ）

visits = new bool[N * 2];

vertices = new Vertex[N * 2];

for (int i = 0; i < N * 2; i++)

Dfs1(i, list);

vertices = vertices.OrderByDescending(_ => _.ID).ToArray();

// 頂点番号からどの強連結成分に属するのか辞書から取得できるようにする

// 先に確定した強連結成分から通し番号をつける

int groupNumber = 0;

Dictionary<int, int> dic = new Dictionary<int, int>();

visits = new bool[N * 2];

foreach (Vertex vertex in vertices)

{

List<int> ret = Dfs2(vertex.Number, rlist);

foreach (int i in ret)

dic.Add(i, groupNumber);

groupNumber++;

}

bool bad = false;

List<long> values = new List<long>();

for (int i = 0; i < N; i++)

{

// 同じ強連結成分内に xi と￢xi に相当する頂点がある場合は論理式は充足できない

if (dic[i] == dic[take_not(i)])

{

bad = true;

break;

}

// 異なる強連結成分内に xi と￢xi が存在する場合は

// xi が true なのか false なのかを確定する

if (dic[i] > dic[take_not(i)])

values.Add(X[i]);

else

values.Add(Y[i]);

}

if (bad)

Console.WriteLine("No");

else

{

Console.WriteLine("Yes");

foreach(int v in values)

Console.WriteLine(v);

}

TwoSAT クラスを定義する

こういう難しい処理は「さあ書け」と言われてすぐにできる自信がありません。2 SAT を解くためのクラスを定義して使い回せるようにします。

class TwoSAT
{
    int N = 0;
    int nextId = 0;
    Vertex[] vertices = { };
    bool[] visits = { };

    // 連結リストと逆向きの連結リスト
    List<int>[] list = null;
    List<int>[] rlist = null;

    class Vertex
    {
        public Vertex(int num, int id)
        {
            Number = num;
            ID = id;
        }
        public int Number = 0;
        public int ID = 0;
    }

    public TwoSAT(int n)
    {
        N = n;

        // 連結リストを生成する
        list = new List<int>[n * 2];
        rlist = new List<int>[n * 2];

        for (int i = 0; i < n * 2; i++)
        {
            list[i] = new List<int>();
            rlist[i] = new List<int>();
        }
    }

    // x ∨ y で指定する
    public void AddConstraintV(bool xTrue, int x, bool yTrue, int y)
    {
        if (!xTrue)
            x = TakeNot(x);
        if (!yTrue)
            y = TakeNot(y);

        list[TakeNot(x)].Add(y);
        list[TakeNot(y)].Add(x);

        rlist[y].Add(TakeNot(x));
        rlist[x].Add(TakeNot(y));
    }

    // x ⇒ y で指定する
    public void AddConstraintArrow(bool xTrue, int x, bool yTrue, int y)
    {
        if (!xTrue)
            x = TakeNot(x);
        if (!yTrue)
            y = TakeNot(y);

        list[x].Add(y);
        list[y].Add(x);
        rlist[y].Add(x);
        rlist[x].Add(y);
    }

    int TakeNot(int x)
    {
        if (x < N)
            return x + N;
        else
            return x - N;
    }

    public List<bool> Solve()
    {
        visits = new bool[N * 2];
        vertices = new Vertex[N * 2];

        for (int i = 0; i < N * 2; i++)
            Dfs1(i, list);

        vertices = vertices.OrderByDescending(_ => _.ID).ToArray();

        int groupNumber = 0;
        Dictionary<int, int> dic = new Dictionary<int, int>();

        visits = new bool[N * 2];
        foreach (Vertex vertex in vertices)
        {
            List<int> ret = Dfs2(vertex.Number, rlist);
            foreach (int i in ret)
                dic.Add(i, groupNumber);

            groupNumber++;
        }

        List<bool> values = new List<bool>();
        for (int i = 0; i < N; i++)
        {
            if (dic[i] == dic[TakeNot(i)])
                return new List<bool>();

            if (dic[i] > dic[TakeNot(i)])
                values.Add(true);
            else
                values.Add(false);
        }
        return values;
    }

    void Dfs1(int vNum, List<int>[] list)
    {
        if (!visits[vNum])
        {
            visits[vNum] = true;
            dfs(vNum);
        }

        void dfs(int num)
        {
            foreach (int i in list[num])
            {
                if (visits[i])
                    continue;
                visits[i] = true;
                dfs(i);
            }
            vertices[num] = new Vertex(num, nextId++);
        }
    }

    List<int> Dfs2(int vNum, List<int>[] list)
    {
        List<int> rets = new List<int>(); // たどり着ける頂点をリストにして返す
        if (!visits[vNum]) // 一度訪問した頂点は対象外
        {
            rets.Add(vNum);
            visits[vNum] = true;
            dfs(vNum);
        }
        return rets;

        void dfs(int num)
        {
            foreach (int i in list[num])
            {
                if (visits[i])
                    continue;
                visits[i] = true;
                dfs(i);
                rets.Add(i);
            }
        }
    }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

class TwoSAT

{

int N = 0;

int nextId = 0;

Vertex[] vertices = { };

bool[] visits = { };

// 連結リストと逆向きの連結リスト

List<int>[] list = null;

List<int>[] rlist = null;

class Vertex

{

public Vertex(int num, int id)

{

Number = num;

ID = id;

}

public int Number = 0;

public int ID = 0;

}

public TwoSAT(int n)

{

N = n;

// 連結リストを生成する

list = new List<int>[n * 2];

rlist = new List<int>[n * 2];

for (int i = 0; i < n * 2; i++)

{

list[i] = new List<int>();

rlist[i] = new List<int>();

}

// x ∨ y で指定する

public void AddConstraintV(bool xTrue, int x, bool yTrue, int y)

{

if (!xTrue)

x = TakeNot(x);

if (!yTrue)

y = TakeNot(y);

list[TakeNot(x)].Add(y);

list[TakeNot(y)].Add(x);

rlist[y].Add(TakeNot(x));

rlist[x].Add(TakeNot(y));

}

// x ⇒ y で指定する

public void AddConstraintArrow(bool xTrue, int x, bool yTrue, int y)

{

if (!xTrue)

x = TakeNot(x);

if (!yTrue)

y = TakeNot(y);

list[x].Add(y);

list[y].Add(x);

rlist[y].Add(x);

rlist[x].Add(y);

}

int TakeNot(int x)

{

if (x < N)

return x + N;

else

return x - N;

}

public List<bool> Solve()

{

visits = new bool[N * 2];

vertices = new Vertex[N * 2];

for (int i = 0; i < N * 2; i++)

Dfs1(i, list);

vertices = vertices.OrderByDescending(_ => _.ID).ToArray();

int groupNumber = 0;

Dictionary<int, int> dic = new Dictionary<int, int>();

visits = new bool[N * 2];

foreach (Vertex vertex in vertices)

{

List<int> ret = Dfs2(vertex.Number, rlist);

foreach (int i in ret)

dic.Add(i, groupNumber);

groupNumber++;

}

List<bool> values = new List<bool>();

for (int i = 0; i < N; i++)

{

if (dic[i] == dic[TakeNot(i)])

return new List<bool>();

if (dic[i] > dic[TakeNot(i)])

values.Add(true);

else

values.Add(false);

}

return values;

}

void Dfs1(int vNum, List<int>[] list)

{

if (!visits[vNum])

{

visits[vNum] = true;

dfs(vNum);

}

void dfs(int num)

{

foreach (int i in list[num])

{

if (visits[i])

continue;

visits[i] = true;

dfs(i);

}

vertices[num] = new Vertex(num, nextId++);

}

List<int> Dfs2(int vNum, List<int>[] list)

{

List<int> rets = new List<int>(); // たどり着ける頂点をリストにして返す

if (!visits[vNum]) // 一度訪問した頂点は対象外

{

rets.Add(vNum);

visits[vNum] = true;

dfs(vNum);

}

return rets;

void dfs(int num)

{

foreach (int i in list[num])

{

if (visits[i])

continue;

visits[i] = true;

dfs(i);

rets.Add(i);

}

このクラスを用いて問題を解くならこうなります。

public class Program
{
    static void Main()
    {
        int N, D;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            D = vs[1];
        }

        int[] X = new int[N];
        int[] Y = new int[N];
        for (int i = 0; i < N; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            X[i] = vs[0];
            Y[i] = vs[1];
        }

        TwoSAT twoSAT = new TwoSAT(N);

        for (int a = 0; a < N; a++)
        {
            for (int b = a + 1; b < N; b++)
            {
                if (Math.Abs(X[a] - X[b]) < D)
                    twoSAT.AddConstraintV(false, a, false, b);
                if (Math.Abs(X[a] - Y[b]) < D)
                    twoSAT.AddConstraintV(false, a, true, b);
                if (Math.Abs(Y[a] - X[b]) < D)
                    twoSAT.AddConstraintV(true, a, false, b);
                if (Math.Abs(Y[a] - Y[b]) < D)
                    twoSAT.AddConstraintV(true, a, true, b);
            }
        }

        List<bool> rets = twoSAT.Solve();

        if (rets.Count == 0)
            Console.WriteLine("No");
        else
        {
            Console.WriteLine("Yes");
            for (int i = 0; i < rets.Count; i++)
            {
                if (rets[i])
                    Console.WriteLine(X[i]);
                else
                    Console.WriteLine(Y[i]);
            }
        }
    }
}

public class Program

{

static void Main()

{

int N, D;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

D = vs[1];

}

int[] X = new int[N];

int[] Y = new int[N];

for (int i = 0; i < N; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

X[i] = vs[0];

Y[i] = vs[1];

}

TwoSAT twoSAT = new TwoSAT(N);

for (int a = 0; a < N; a++)

{

for (int b = a + 1; b < N; b++)

{

if (Math.Abs(X[a] - X[b]) < D)

twoSAT.AddConstraintV(false, a, false, b);

if (Math.Abs(X[a] - Y[b]) < D)

twoSAT.AddConstraintV(false, a, true, b);

if (Math.Abs(Y[a] - X[b]) < D)

twoSAT.AddConstraintV(true, a, false, b);

if (Math.Abs(Y[a] - Y[b]) < D)

twoSAT.AddConstraintV(true, a, true, b);

}

List<bool> rets = twoSAT.Solve();

if (rets.Count == 0)

Console.WriteLine("No");

else

{

Console.WriteLine("Yes");

for (int i = 0; i < rets.Count; i++)

{

if (rets[i])

Console.WriteLine(X[i]);

else

Console.WriteLine(Y[i]);

}

TwoSAT クラスを用いて問題を解いてみる

No.274 The Wall

1×1 のブロックが横に M 個連なった 1×M のブロックがある。
ブロックは基本白色であるが左から L 番目から左から R 番目(0-index)までの連続したブロックはピンク色である。ブロックは180度回転することもできる。

横の長さが同じ 1×M の N 本のブロックが与えられる。
それぞれのブロックはそれぞれピンク色の連続した領域を1つ持つ。
N 本のブロックを上に積んでいき良い壁を作りたい。
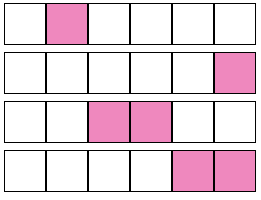
良い壁とは縦の列でブロックを見たときピンク色のブロックが 1 つ以下のものをいう。

以下のようなブロックが与えられたとする。

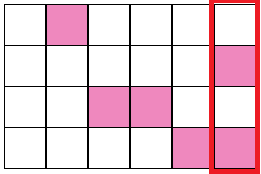
これをそのまま積み上げたものがこれであるが、これは「良い壁」ではない。一番右の列にピンク色のブロックがふたつある。

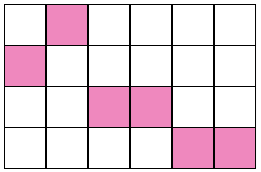
上から2段目のものを 180 度反転した。これは「良い壁」である。

与えられる N 本のブロックをすべて積んで良い壁を作れるか判定せよ。

入力されるデータ
N M
L_0 R_0
L_1 R_1
…
L_N-1 R_N-1

（ただし、
2 ≦ N ≦ 2000
2 ≦ M ≦ 4000
L_i 一番左のピンク色のブロックの位置
R_i 一番右のピンク色のブロックの位置）
0 ≦ L_i ≦ R_i ≦ M ）

これはブロックをそのまま置くか180度回転させて置くかの組み合わせで「良い壁」を作ることができるかという充足可能性問題です。

a ＜ b としてすべての a, b の組み合わせを考えてみることにします。x は a をそのまま置くとき true, 180 度反転させて置く場合 false です。y は b をそのまま置くかどうかです。

（1）a と b がそのままだと衝突しないし、b を 180 度回転しても衝突しない場合
この 2 つは絶対に干渉しないのでなにもしない。
（2）a と b がそのままだと衝突しないが、b を 180 度回転すると衝突する場合
両方ともそのままか両方とも 180 度回転させないといけないので x ⇒ y, ￢x ⇒ y
（3）a と b がそのままだと衝突するが、b を 180 度回転すると衝突しない場合
片方だけ 180 度回転させないといけないので￢x ⇒ y, x ⇒ ￢y
（4）a と b がそのままだと衝突し、b を 180 度回転しても衝突する場合
どうやっても「悪い壁」しか作れないので “No”を出力する

この場合は ∨ ではなく ⇒ を使ったほうがわかりやすいです。

public class Program
{
    // TwoSAT クラスは上記と同じなので省略

    static void Main()
    {
        int N, M;
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            N = vs[0];
            M = vs[1];
        }

        int[] L = new int[N];
        int[] R = new int[N];
        for (int i = 0; i < N; i++)
        {
            int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();
            L[i] = vs[0];
            R[i] = vs[1];
        }

        TwoSAT twoSAT = new TwoSAT(N);

        for (int a = 0; a < N; a++)
        {
            for (int b = a + 1; b < N; b++)
            {
                bool b1 = (R[b] < L[a] || R[a] < L[b]);
                bool b2 = (M - L[b]- 1 < L[a] || R[a] < M - R[b]-1);
                if (b1 && !b2) // 片方だけ反転すると干渉する
                {
                    twoSAT.AddConstraintArrow(true, a, true, b);
                    twoSAT.AddConstraintArrow(false, a, false, b);
                }
                if (!b1 && b2) // 片方だけ反転させないと干渉する
                {
                    twoSAT.AddConstraintArrow(false, a, true, b);
                    twoSAT.AddConstraintArrow(true, a, false, b);
                }
                if (!b1 && !b2) // どうやってもダメ
                {
                    Console.WriteLine("NO");
                    return;
                }
            }
        }

        List<bool> rets = twoSAT.Solve();

        if (rets.Count == 0)
            Console.WriteLine("NO");
        else
            Console.WriteLine("YES");
    }
}

public class Program

{

// TwoSAT クラスは上記と同じなので省略

static void Main()

{

int N, M;

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

N = vs[0];

M = vs[1];

}

int[] L = new int[N];

int[] R = new int[N];

for (int i = 0; i < N; i++)

{

int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray();

L[i] = vs[0];

R[i] = vs[1];

}

TwoSAT twoSAT = new TwoSAT(N);

for (int a = 0; a < N; a++)

{

for (int b = a + 1; b < N; b++)

{

bool b1 = (R[b] < L[a] || R[a] < L[b]);

bool b2 = (M - L[b]- 1 < L[a] || R[a] < M - R[b]-1);

if (b1 && !b2) // 片方だけ反転すると干渉する

{

twoSAT.AddConstraintArrow(true, a, true, b);

twoSAT.AddConstraintArrow(false, a, false, b);

}

if (!b1 && b2) // 片方だけ反転させないと干渉する

{

twoSAT.AddConstraintArrow(false, a, true, b);

twoSAT.AddConstraintArrow(true, a, false, b);

}

if (!b1 && !b2) // どうやってもダメ

{

Console.WriteLine("NO");

return;

}

List<bool> rets = twoSAT.Solve();

if (rets.Count == 0)

Console.WriteLine("NO");

else

Console.WriteLine("YES");

}

強連結成分分解をして充足可能性問題を解く

充足可能性問題とは？

Implication グラフ

強連結成分分解をして充足可能性問題を解いてみる

H – Two SAT

実装してみる

TwoSAT クラスを定義する

TwoSAT クラスを用いて問題を解いてみる

No.274 The Wall

鳩でも分かるC#管理人からのお願い

コメントについて

管理人のモチベーションアップのために

コメントをどうぞ