D – Grid and Magnet
D – Grid and Magnetはこんな問題です。
H 行 W 列のマス目があり、いくつか(0 個のこともある)のマスには磁石が置かれています。
マス目の状態は H 個の 長さ W の文字列 S_1, S_2, …, S_H で表され、 S_i の j 文字目が # のとき上から
i 行目かつ左から j 列目のマスには磁石が置かれていることを、 . のとき何も置かれていないことを表しています。高橋君は鉄の鎧を着ており、あるマスにいるとき次のように移動することができます。
現在いるマスの上下左右に隣り合うマスのいずれかに磁石が置かれているとき、どこへも移動することができない。
そうでないとき、上下左右に隣り合うマスのいずれかを選んでそのマスに移動することができる。
ただし、マス目の外に移動することはできない。磁石が置かれていない各マスについて、そのマスの自由度を、「最初高橋くんがそのマスにいるとき、そこから移動を繰り返して到達できるマスの個数」として定義します。 マス目のうち磁石が置かれていないマスの中における、マスの自由度の最大値を求めてください。
ただし、自由度の定義において、「移動を繰り返して到達できるマス」とは、最初にいるマスからそのマスまで移動を繰り返して到達する方法(1 回も移動しないものも含む)が 1 つ以上存在するようなマスのことであり、 最初のマスから始めてすべてのそのようなマスを巡るような移動方法が存在する必要はありません。特に(磁石の置かれていない)各マス自身は、そのマスから「移動を繰り返して到達できるマス」につねに含まれることに注意してください。
入力されるデータ
H W
S_1
S_2
…
S_H
(ただし、1 ≦ H, W ≦ 1000
S_i は . と # のみからなる長さ W の文字列 )
島探しに似た問題ですが、# の隣を数えるときに注意が必要です。図のように # の隣は複数回数えなければならないのです。
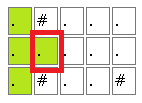
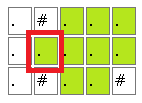
単純に2回カウントしない方法では解が得られないことと、同じ部分を何度もチェックしているとTLE(Time Limit Exceeded – 要は「時間切れ」) してしまうので、これをうまく回避するのがこの問題の肝であるように思われます。
探索の始点をずらすだけでは同じ領域を何度も探索してしまわないようにするのはどうすればよいでしょうか? マス A から マス B へ移動でき、マス B に隣接したマスに磁石が置かれていない時、マス A とマス B の自由度は等しいことはわかります。そこで最初に同じ領域を何度も探索しないように探索の始点になる部分だけを取得することで二回チェックをする部分を減らせないかと考えました。これでTLE を回避しようとしているのですが、残念ながら TLE してしまいます。
工夫したがTLEしてしまうコード
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 |
using System; using System.Collections.Generic; using System.Linq; class Cell { public Cell(int row, int col) { Row = row; Col = col; } public int Row = 0; public int Col = 0; } class Program { static void Main() { int H, W; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); H = vs[0]; W = vs[1]; } char[,] map = new char[H, W]; for (int row = 0; row < H; row++) { char[] vs = Console.ReadLine().ToArray(); for (int col = 0; col < W; col++) map[row, col] = vs[col]; } // 磁石のとなりを '*' に置き換える for (int row = 0; row < H; row++) { for (int col = 0; col < W; col++) { if (map[row, col] == '#') { if (row > 0 && map[row - 1, col] != '#') map[row - 1, col] = '*'; if (row < H - 1 && map[row + 1, col] != '#') map[row + 1, col] = '*'; if (col > 0 && map[row, col - 1] != '#') map[row, col - 1] = '*'; if (col < W - 1 && map[row, col + 1] != '#') map[row, col + 1] = '*'; } } } // 探索の始点をずらすだけでは同じ領域を何度も探索してしまうので // 最初に同じ領域を何度も探索しないように探索の始点になる部分だけを取得する List<Cell> cells = BFS(H, W, map); // 探索の始点になる部分が取得できたので、これを始点に探索をする int ans = 1; foreach (Cell cell in cells) { int c = BFS2(H, W, cell.Row, cell.Col, map); ans = Math.Max(ans, c); } Console.WriteLine(ans); } // 一度チェックしたマスと '#' と '*' 以外の部分を探索する static List<Cell> BFS(int H, int W, char[,] map) { List<Cell> firsts = new List<Cell>(); bool[,] visit = new bool[H, W]; for (int row = 0; row < H; row++) { for (int col = 0; col < W; col++) { if (visit[row, col] || map[row, col] == '#' || map[row, col] == '*') continue; Queue<int> qx = new Queue<int>(); Queue<int> qy = new Queue<int>(); qx.Enqueue(col); qy.Enqueue(row); visit[row, col] = true; firsts.Add(new Cell(row, col)); int[] dx = { 0, 0, 1, -1 }; int[] dy = { 1, -1, 0, 0 }; while (qx.Count > 0) { int x = qx.Dequeue(); int y = qy.Dequeue(); for (int i = 0; i < 4; i++) { int nx = x + dx[i]; int ny = y + dy[i]; if (nx < 0 || ny < 0 || nx >= W || ny >= H) continue; if (map[ny, nx] == '#' || map[ny, nx] == '*') continue; if (visit[ny, nx]) continue; visit[ny, nx] = true; qx.Enqueue(nx); qy.Enqueue(ny); } } } } return firsts; } // '#' による動作の制約も考慮した行動範囲を取得する static int BFS2(int H, int W, int sr, int sc, char[,] map) { bool[,] visit = new bool[H, W]; Queue<int> qx = new Queue<int>(); Queue<int> qy = new Queue<int>(); qx.Enqueue(sc); qy.Enqueue(sr); visit[sr, sc] = true; int[] dx = { 0, 0, 1, -1 }; int[] dy = { 1, -1, 0, 0 }; int count = 0; // 行動範囲をカウントする while (qx.Count > 0) { int x = qx.Dequeue(); int y = qy.Dequeue(); count++; // '*' へは移動できるが '*' からは移動できない if (map[y, x] == '*') continue; for (int i = 0; i < 4; i++) { int nx = x + dx[i]; int ny = y + dy[i]; if (nx < 0 || ny < 0 || nx >= W || ny >= H) continue; if (map[ny, nx] == '#') continue; if (visit[ny, nx]) continue; visit[ny, nx] = true; qx.Enqueue(nx); qy.Enqueue(ny); } } return count; } } |
改善策
上記のコードで TLE するのであればどうすればよいのでしょうか? 探索しなくてよい部分の処理を省略することで時間短縮をする以外ありません。問われているのは行動範囲の最大値です。なので最初の BFS メソッドのなかでだいたいの数(磁石の隣を除く領域の広さ)をカウントします。磁石の隣にも移動できることを考慮する場合、考慮しない場合の2倍に2を加えた数が上限となります。
なので磁石の隣を除く領域の広さを取得しておき、ソートします。磁石の隣にも移動できる部分を探索する処理をする前に明らかに解の候補にならないものは弾きます。そうすることで制限時間内に間にあうようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 |
class Cell { public Cell(int row, int col) { Row = row; Col = col; } public int Row = 0; public int Col = 0; public int Value = 0; // 追加 } class Program { // BFS2(int H, int W, int sr, int sc, char[,] map) メソッドは同じなので省略 static List<Cell> BFS(int H, int W, char[,] map) { List<Cell> firsts = new List<Cell>(); bool[,] visit = new bool[H, W]; for (int row = 0; row < H; row++) { for (int col = 0; col < W; col++) { if (visit[row, col] || map[row, col] == '#' || map[row, col] == '*') continue; Queue<int> qx = new Queue<int>(); Queue<int> qy = new Queue<int>(); qx.Enqueue(col); qy.Enqueue(row); visit[row, col] = true; int value = 1; // 磁石の隣以外を数える Cell first = new Cell(row, col); int[] dx = { 0, 0, 1, -1 }; int[] dy = { 1, -1, 0, 0 }; while (qx.Count > 0) { int x = qx.Dequeue(); int y = qy.Dequeue(); for (int i = 0; i < 4; i++) { int nx = x + dx[i]; int ny = y + dy[i]; if (nx < 0 || ny < 0 || nx >= W || ny >= H) continue; if (map[ny, nx] == '#' || map[ny, nx] == '*') continue; if (visit[ny, nx]) continue; visit[ny, nx] = true; value++; qx.Enqueue(nx); qy.Enqueue(ny); } } first.Value = value; // 磁石の隣を除く面積を記録する firsts.Add(first); } } return firsts; } static void Main() { int H, W; { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); H = vs[0]; W = vs[1]; } char[,] map = new char[H, W]; for (int row = 0; row < H; row++) { char[] vs = Console.ReadLine().ToArray(); for (int col = 0; col < W; col++) map[row, col] = vs[col]; } for (int row = 0; row < H; row++) { for (int col = 0; col < W; col++) { if (map[row, col] == '#') { if (row > 0 && map[row - 1, col] != '#') map[row - 1, col] = '*'; if (row < H - 1 && map[row + 1, col] != '#') map[row + 1, col] = '*'; if (col > 0 && map[row, col - 1] != '#') map[row, col - 1] = '*'; if (col < W - 1 && map[row, col + 1] != '#') map[row, col + 1] = '*'; } } } List<Cell> cells = BFS(H, W, map); cells = cells.OrderByDescending(_ => _.Value).ToList(); // 大きい順にソート int ans = 1; foreach (Cell cell in cells) { if (ans > cell.Value * 2 + 2) // 暫定的な解と比較して解の候補になり得ないものは弾く break; int c = BFS2(H, W, cell.Row, cell.Col, map); ans = Math.Max(ans, c); } Console.WriteLine(ans); } } |
