最近AtCoderにハマっています。paizaラーニングのpaizaランクは最高位のSランクですが、AtCoderではなかなか底辺の「灰色」から抜け出せません。問題もpaizaラーニングとは比べ物にならないくらい難しいです。
トヨタ自動車はクルマを作っている会社であり、ITとの関係でいえば自動運転が浮かぶ方が多いと思いますが、実は他にも箇所(生産・物流・調達・販売)にもITが活用されていて、これらの最適化を追求しているそうです。
出題された問題は全部で7問。簡単な問題から上級者でも考え込んでしまうような難しい問題まで幅広くあります。配点は
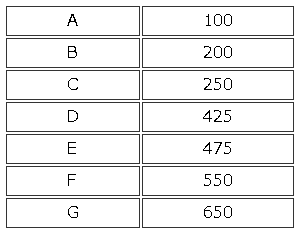
です。当然難しい問題ほど配点は高くなります。
ではどんな問題が出題されたのかをみてみましょう。
第1問 A – Penalty Kick
髙橋君はサッカーの試合で N 回ペナルティキックを蹴ります。
i 回目のペナルティキックでは、i が 3 の倍数の場合は失敗しそれ以外の場合は成功します。
髙橋君がペナルティキックを蹴ったときの結果を出力してください(成功したらo、失敗したらx、これを並べる)。入力
N (ただし 1 ≦ N ≦ 100)出力
ooxoox(N が 6 の場合)
という問題です。
Nが最大で100なので普通に i = 1 から i = N までループを回して、i が 3の倍数のときは ‘x’ を追加して それ以外のときは ‘o’ を追加する。それだけで充分だと思います。N がもっと大きな数の場合はもっと効率のいいやり方を考えないといけないのかもしれませんが、N が 100以下なのでこれでよいと思います。
なんの工夫もないコードですが、テストはとおります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N = int.Parse(Console.ReadLine()); string s = ""; for (int i = 1; i <= N; i++) { if(i % 3 == 0) s += "x"; else s += "o"; } Console.WriteLine(s); } } |
第2問 B – Farthest Point
xy 平面上に 1 から N までの番号が付いた N 個の点があります。点 i は座標 (X[i], Y[i]) にあり、相異なる 2 点の座標は異なります。
各点について、その点からの距離が最大である点を求めてその点の番号を出力してください。 ただし、距離が最大である点が複数ある場合はその中で最も番号が小さい点の番号を出力してください。
入力されるデータ
N (ただし 2 ≦ N ≦ 100)
X_1 Y_1
X_2 Y_2
X_3 Y_3
…
X_N Y_N
これも N が最大で100なので全部愚直に調べても時間以内に終わると思います。また知りたいのは距離そのものではなく距離の大小関係なので、距離の2乗を比較しています(これでも大小関係は変わらない)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N = int.Parse(Console.ReadLine()); // 点のXY座標を配列に格納する double[] xs = new double[N]; double[] ys = new double[N]; for (int i = 0; i < N; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); xs[i] = vs[0]; ys[i] = vs[1]; } for (int i = 0; i < N; i++) { int ans = 0; double max2 = 0; // 始点のXY座標 double x1 = xs[i]; double y1 = ys[i]; for (int k = 0; k < N; k++) { if (k == i) continue; // 終点のXY座標 double x2 = xs[k]; double y2 = ys[k]; double d2 = Math.Pow(x1 - x2, 2) + Math.Pow(y1 - y2, 2); // 最大値が更新されたら更新する if (max2 < d2) { max2 = d2; ans = k + 1; } } // 最終的にもっとも遠い点の番号を出力する Console.WriteLine(ans); } } } |
第3問 C – Colorful Beans
N 種類のビーンズが 1 粒ずつあります。i 種類目のビーンズはおいしさが A[i] で色が C[i] です。ビーンズは混ぜられており、色でしか区別することができません。
あなたはビーンズの色を 1 つ選び、その色のビーンズをどれか 1 粒食べます。ビーンズの色をうまく選ぶことで、食べる可能性のあるビーンズのおいしさの最小値を最大化してください。
入力
N (ただし 1 ≦ N ≦ 200,000)
A_1 C_1
A_2 C_2
A_3 C_3
A_4 C_4
……
A_N C_N
最初問題文を読んだとき意味がわからなかったのですが、これは「同じ色でグループをつくり、そのなかで最小値を求めよ。最後に各グループで算出された最小値の最大値を求めよ」という問題です。
どうやって同じ色でグループを作るか、そのグループ内で最小値を計算するかですが、鳩が思いついたのはDictionaryクラスを使う方法です。色をKeyにして、登録されていない色であれば辞書に追加し、すでに追加されているならValueと新しいビーンズのおいしさを比較して少ないほうでValueの値を更新するという考え方です。最後に辞書のなかのValueの最大値を計算します。
各色について、N 種類すべてのビーンズを確認する方法でも正しい答えを得られますが、色の種類数も最大で N 種類あることになるので、全探索でこの処理をしようとすると、計算量はO(N ^ 2) になります。これでは間に合わないケースもでてきます。Dictionaryクラスや連想配列を使う方法であれば O(NlogN) となり、N が 200,000だったとしても充分間に合います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
using System; using System.Collections.Generic; using System.Linq; class Program { static void Main() { int N = int.Parse(Console.ReadLine()); Dictionary<long, long> dic = new Dictionary<long, long>(); for (int i = 0; i < N; i++) { int[] vs = Console.ReadLine().Split().Select(_ => int.Parse(_)).ToArray(); int a = vs[0]; int c = vs[1]; if(!dic.ContainsKey(c)) dic.Add(c, a); else dic[c] = Math.Min(dic[c], a); } long max = dic.Max(_ => _.Value); Console.WriteLine(max); } } |
ということで、ここまでトントン拍子に進んで来たのですが、鳩の快進撃もここまで。次の問題で捕まってしまいました。次回はその反省文を書くことにします。
