Contents
Cマガ電脳クラブとタンク・チェンジ
『C MAGAZINE』は1989年10月号から2006年4月号まで全199号が発行されたプログラミング技術情報誌です。そのなかにCマガ電脳クラブというコーナーがあり、出題された問題をC言語で作ったプログラムで解き、応募するというコーナーがあります。
タンク・チェンジはCマガ電脳クラブ(第127回)で出題された問題です。内容は以下のようなものです。
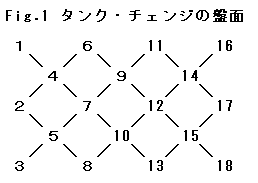
Fig.1のような盤を用意し,A軍の戦車3台とB軍の戦車3台をそれぞれ1,2,3と16,17,18の円に配置する。
直線は道路を,円は広場を表す。1.A軍を先手として、3台の戦車のうちのどれかを1台動かす。これを交互に繰り返す。
2.戦車は道路に沿って広場から広場へと移動できる。1つの広場には1台しか入れない。
3.戦車は動き始めたら止まるまで直進しかできない。いくつ先の広場で止まるかは自由だが、通り道にほかの戦車がいる場合はそれより先には進めない。いくつ進んでもこれが「1手」。
4.止まった広場が敵軍の戦車から道路を介してまっすぐに見える場合には撃たれてしまう。
以上の条件で両軍が撃ち合うことなく戦車をそっくり入れ替えたい。最低何手で完成できるだろうか。その移動手順の一例も示すこと。
面白そうな問題ですが当時はどうやって考えていいかわからず、ずっとモヤモヤしていました。今回は動的計画法でこの問題を解くことにします。
マップについて
考えられる手で次のマップをつくります。マップはこれまでの手数と手番とをセットにして辞書に格納します。もし同一局面が発生した場合、これまでの手数よりも長いものであれば捨ててしまいます(問いでは最短を問われているので同一局面で既知のものよりも長手順となるものは考えるだけ無駄)。通常のリストではなく辞書を使うのは検索時の速度が速く、同じものがあるかどうかがすぐにわかるからです。
まず戦車が存在する広場ですが、問題文では1~18までの番号がつけられています。どの番号の広場からどの番号の広場に戦車が移動できるのかを考えやすくするために番号を変えます。
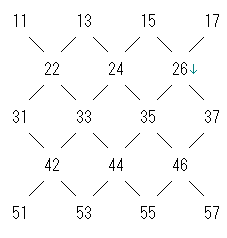
これで現在の広場の右上、右下、左上、左下に位置する広場の番号は、現在の広場の番号にそれぞれ9を引く、11を足す、11を引く、9を足すことで得られますし、1の位は1~7、10の位は1~5のものを考えるだけでよくなりました。
Handクラスの定義
次の手を意味するHandクラスを定義します。Fromの位置にある戦車をToに移動させるという意味です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
using System; using System.Collections.Generic; using System.Linq; public class Hand { public Hand(int from, int to) { From = from; To = to; } public int From { get; } public int To { get; } } |
Statusクラスの定義
次に戦車を移動させたり現在の状態を取得するためのStatusクラスを定義します。
|
1 2 3 4 5 6 7 8 |
public class Status { public int Turn { private set; get; } // A軍:0 B軍:1 public int TurnCount { private set; get; } public List<int>[] TankPositions { private set; get; } public Status PrevStatus { private set; get; } } |
プロパティは以上です。
初期化
以下は初期の位置に戦車を配置するメソッドです。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
public class Status { public void SetStartPositions() { Turn = 0; TurnCount = 0; TankPositions = new List<int>[2]; TankPositions[0] = new List<int> { 11, 31, 51 }; TankPositions[1] = new List<int> { 17, 37, 57 }; } } |
完了確認
戦車を移動させたら陣地の入れ替えが完了しているかを調べます。TankPositions[0]とTankPositions[1]の内容が入れ替わっていれば処理は完了していることになります。
|
1 2 3 4 5 6 7 8 9 10 11 |
public class Status { public bool IsFinish() { if ( TankPositions[0][0] == 17 && TankPositions[0][1] == 37 && TankPositions[0][2] == 57 && TankPositions[1][0] == 11 && TankPositions[1][1] == 31 && TankPositions[1][2] == 51 ) return true; else return false; } } |
移動できる場所を探す
GetNextsメソッドは戦車を移動できる場所を返します。ただし敵の戦車に撃たれない安全な位置かどうかは判定していません。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
public class Status { int[] GetNexts(int position) { List<int> list = new List<int>(); int turn = Turn; int[] vs = { 11, -11, 9, -9 }; foreach (int value in vs) { int temp = position; while (true) { temp += value; int one = temp % 10; int ten = temp / 10; if (1 <= one && one <= 7 && 1 <= ten && ten <= 5) { if (!TankPositions[turn].Any(_ => _ == temp)) list.Add(temp); else break; } else break; } } return list.ToArray(); } } |
安全な位置とはその位置から敵の戦車に直接たどりつくことができない位置です。GetSafeNextsメソッドは現在の位置から移動できる位置であるとともに、敵に撃たれることのない安全な位置の配列を返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
public class Status { public int[] GetSafeNexts(int position) { int[] nexts = GetNexts(position); return nexts.Where(x => IsSafe(x)).ToArray(); } public bool IsSafe(int position) { // 引数の位置から敵にたどりつけるのであれば敵に撃たれる位置。 // そのような位置でないなら安全な位置である。 List<int> enemiesPositions = Turn == 0 ? TankPositions[1] : TankPositions[0]; List<int> dangers = new List<int>(); foreach (int enemyPosition in enemiesPositions) { int[] nexts = GetNexts(enemyPosition); dangers.AddRange(nexts); } return !dangers.Any(_ => _ == position); } } |
着手可能な手を探す
GetHandsメソッドは着手可能な手のリストを返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
public class Status { public List<Hand> GetHands() { List<Hand> hands = new List<Hand>(); List<int> positions = TankPositions[Turn]; foreach (int position in positions) { int[] nexts = GetSafeNexts(position); foreach (int next in nexts) { if (!positions.Any(_ => _ == next)) hands.Add(new Hand(position, next)); } } return hands; } } |
着手後の状態を取得する
GetResultメソッドは着手後の状態を返します。
ここではまず移動後の新しい戦車の位置を取得します。移動前の戦車の位置がTankPositions[0]かTankPositions[1]に格納されているはずなので、そのコピーのなかからこれを削除し、かわりに移動後の位置を追加します。できない場合は移動対象はリストのなかにはないのでなにもしません。
そのあと前の状態から必要なデータを新しい状態に引き継ぎます。着手した以上は手数が1つ増えるのでTurnCountをインクリメントし、手番を交代します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
public class Status { public Status GetResult(Hand hand) { // 新しい戦車の位置を取得する List<int>[] tankPositions = new List<int>[2]; for (int i = 0; i < 2; i++) { List<int> positions = TankPositions[i].ToList(); if (positions.Remove(hand.From)) positions.Add(hand.To); tankPositions[i] = positions.OrderBy(_ => _).ToList(); } Status status = new Status(); status.Turn = this.Turn == 0 ? 1 : 0; // 手番を交代する status.TurnCount = this.TurnCount + 1; // 手数を増やす status.TankPositions = tankPositions; // 新しい戦車の位置をセット status.PrevStatus = this; // 最短手順の一例を示さなければならないので前の状態を保存しておく return status; } } |
TankPositionsToLongメソッドは手番と戦車の位置をlong型の変数に変換します。これはStatusオブジェクトを辞書に登録するときのキーに利用します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
public class Status { public long TankPositionsToLong() { return TankPositions[0][0] + TankPositions[0][1] * 100 + TankPositions[0][2] * 10000 + TankPositions[1][0] * 1000000 + TankPositions[1][1] * 100000000 + TankPositions[1][2] * 10000000000 + Turn * 1000000000000; } } |
Solverクラスの定義
解を得る処理をするSolverクラスを定義します。
幅優先探索と動的計画法で求解
最初に初期状態のStatusオブジェクトを生成し、キューに格納します。ループのなかでキューのなかからデータを取り出し、そのオブジェクトの次の手を探します。手が見つかったら着手してその結果を辞書に登録しますが、既知の局面が見つかった場合は無視します。
着手後のオブジェクトからIsFinishメソッドを呼び出してtrueを返したときは処理は終了です。またそれよりもまえにキューが空になったら手詰まりで解は存在しないことになりますが、実際に処理をしてみると解は存在することがわかります。
処理が終わったらIsFinishメソッドを呼び出してtrueを返したオブジェクトを返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
class Solver { Status BFS() { Dictionary<long, Status> KeyValuePairs = new Dictionary<long, Status>(); Status startStatus = new Status(); startStatus.SetStartPositions(); Queue<Status> queue = new Queue<Status>(); queue.Enqueue(startStatus); KeyValuePairs.Add(startStatus.TankPositionsToLong(), startStatus); bool find = false; Status lastStatus = null; while (queue.Count > 0 && !find) { Status status = queue.Dequeue(); List<Hand> hands = status.GetHands(); foreach (Hand hand in hands) { Status newStatus = status.GetResult(hand); if (newStatus.IsFinish()) { find = true; lastStatus = newStatus; break; } long key = newStatus.TankPositionsToLong(); if (!KeyValuePairs.ContainsKey(key)) { KeyValuePairs.Add(key, newStatus); queue.Enqueue(newStatus); } else { if (KeyValuePairs[key].TurnCount > newStatus.TurnCount) { KeyValuePairs[key] = newStatus; queue.Enqueue(newStatus); } } } } return lastStatus; } } |
最短手順の一例を求める
BFSメソッドが返したオブジェクトを逆順にたどって手順を求めます。PrevStatusプロパティがnullならそれが初期状態のオブジェクトです。これまでにリストに格納したデータを逆順にします。これで最初から最後までの手順がわかります。
Status.PrevStatus.TankPositionsとStatus.TankPositionsを比較するとどの戦車を移動させたかがわかります。あとは結果を表示するだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
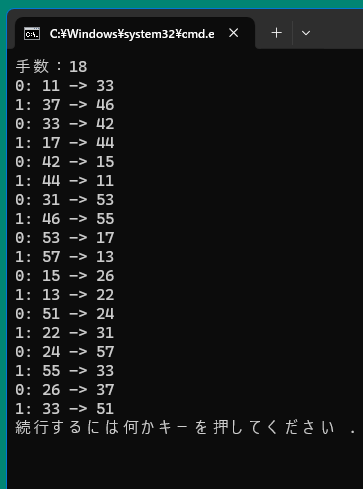
class Solver { public void Solve() { Status lastStatus = BFS(); Console.WriteLine("手数:" + lastStatus.TurnCount); List<Status> statuses = new List<Status>(); statuses.Add(lastStatus); while (true) { Status prevStatus = lastStatus.PrevStatus; if (prevStatus == null) break; lastStatus = prevStatus; statuses.Add(prevStatus); } statuses.Reverse(); statuses = statuses.Skip(1).ToList(); foreach (Status status in statuses) { int prevTurn = status.PrevStatus.Turn; int newPosition = 0; int oldPosition; List<int> prevPositions = status.PrevStatus.TankPositions[prevTurn].ToList(); foreach (int pos in status.TankPositions[prevTurn]) { if (!prevPositions.Remove(pos)) newPosition = pos; } oldPosition = prevPositions[0]; Console.WriteLine($"{prevTurn}: {oldPosition} -> {newPosition}"); } } } |
仕上げ
最後にSolverオブジェクトを生成してMainメソッドのなかで解を求め表示させます。実行時間はどんなPCを使うかにもよりますが、管理人の環境では約1秒でした。
|
1 2 3 4 5 6 7 8 |
class Program { static void Main() { Solver solver = new Solver(); solver.Solve(); } } |