C# 最大長方形問題を解く 面積が最大の長方形を見つけるアルゴリズム関連の話。今回は長方形ではなく正方形を探します。この場合はどうすればいいのでしょうか?

全探索をする方法
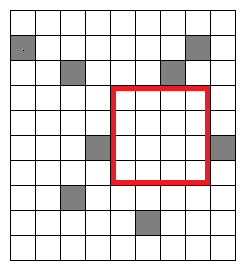
まずは何も考えずに全探索をする方法を考えます。二重ループで正方形の左上の座標を求め、そこから一辺の長さをだんだん長くしながら正方形をつくることができるかを考えます。mapの’#’が正方形のなかに含まれてはいけない部分です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
using System; using System.Linq; using System.Collections.Generic; class Program { static void Main() { string[] map = { ".........", "#......#.", "..#...#..", ".........", ".........", "...#....#", ".........", "..#......", ".....#...", }; int rowCount = map.Length; int colCount = map[0].Length; int max_width = 0; for (int row = 0; row < rowCount; row++) { for (int col = 0; col < colCount; col++) { int width = 0; while (true) { width++; // 左上の座標が(col, row)であり、一辺の長さがwidthである正方形の内部はすべて'.'か調べる for (int row2 = row; row2 <= row + width; row2++) { for (int col2 = col; col2 <= col + width; col2++) { if (row2 >= rowCount || col2 >= colCount || map[row2][col2] != '.') goto end_while; // 多重ループから一気に抜けたいので仕方なくgoto文を使う } } } end_while: if(max_width < width) max_width = width; } } Console.WriteLine($"一辺の長さは {max_width} である"); } } |
全体が5重ループ(O(n^5))になっています。しかもgoto文のおまけ付きです。goto文は一律不可ではなく、多重ループから一気に抜けるときは使ってもいいのではないかという話は聞きますが、そもそも何重ものループができてしまう段階でおかしいと考えたほうがいいのではないでしょうか?
動的計画法で解く
この問題は動的計画法を用いればO(n^2)のアルゴリズムで解くことができます。正方形の左上に目がいきがちですが、ここでは右下の座標に着目します。

二次元配列 widths[y][x] を用意します。これは (x, y) から左上に向かってできる最大の正方形の一辺の長さを表わします。すると widths[y][x] の値はすでに確定している widths[y – 1][x], widths[y][xy – 1], widths[yy – 1][xy – 1]の最小値に1を足した数であることに気がつきます。上端と左端の部分は ‘#’(正方形に含まれてはいけない部分)である場合は0、そうでない場合は1で初期化しておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
using System; using System.Linq; using System.Collections.Generic; class Program { static void Main() { string[] map = { ".........", "#......#.", "..#...#..", ".........", ".........", "...#....#", ".........", "..#......", ".....#...", }; int rowCount = map.Length; int colCount = map[0].Length; List<int[]> valuesList = new List<int[]>(); for (int row = 0; row < rowCount; row++) valuesList.Add(new int[colCount + 1]); // 二次元配列の上端部分を初期化 for (int row = 0; row < rowCount; row++) valuesList[row][0] = map[row][0] == '.' ? 1 : 0; // 二次元配列の左端部分を初期化 for (int col = 0; col < colCount; col++) valuesList[0][col] = map[0][col] == '.' ? 1 : 0; int max = 0; // 正方形の一辺の長さの最小値 int x = 0; // 正方形の左上部分のX座標 int y = 0; // 同 Y座標 for (int row = 1; row < rowCount; row++) { for (int col = 1; col < colCount; col++) { if (row == 0) valuesList[0][col] = map[0][col] == '.' ? 1 : 0; else { if (map[row][col] == '#') valuesList[row][col] = 0; else { List<int> values = new List<int>(); values.Add(valuesList[row - 1][col]); values.Add(valuesList[row][col - 1]); values.Add(valuesList[row - 1][col - 1]); valuesList[row][col] = values.Min() + 1; if (max < valuesList[row][col]) { max = valuesList[row][col]; x = col - max + 1; y = row - max + 1; } } } } } Console.WriteLine($"(X={x}, Y={y}) {max}*{max}"); } } |
最大正方形問題の応用例
最大正方形問題を解くことができるようになったわけですが、これを利用する場面としてどのようなものがあるのでしょうか?
最大正方形問題は、コンピュータビジョン、画像処理、地理情報システム、最適化、ゲーム開発などのさまざまな分野で応用されています。以下に、その応用例のいくつかを挙げます。
画像処理
画像内のオブジェクトや特徴領域を検出する際に使用されます。例えば、特定のオブジェクトが含まれる最大の正方形領域を見つけることで、そのオブジェクトの境界ボックスを検出することができます。
地理情報システム (GIS)
地図上の地域や地形の特定の領域を表すために使用されます。最大正方形問題を解くことで、地理的なエリアの最大範囲を特定することができます。
最適化問題
配置や配置の最適化に関連して、最大の利用可能スペースを見つけるために使用されます。例えば、工場の機械配置や建物の間取りの最適化に利用されます。
ゲーム開発
ゲーム内のマップやレベル設計において、プレイヤーの移動可能な領域や障害物の配置に関連して利用されます。最大正方形領域を見つけることで、プレイヤーが移動できる安全な領域を決定することができます。
データ解析
表形式のデータやグリッド状のデータにおいて、特定のパターンや構造を見つけるために使用されます。例えば、地震発生地域の特定や、顧客行動のパターン解析などに利用されます。
これらは一部の応用例であり、最大正方形問題はさまざまな分野で幅広く活用されています。
