Ford-Fulkerson法と最大流問題
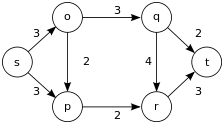
最大流問題(最大フロー問題)とは、単一の始点から単一の終点へのフローネットワークで最大となるフローを求める問題です。各地点が水道管でつながっていて、どのように水を流せば一番多くの水を流せるかという問題と考えることもできます。
下の図はで頂点が6つ、頂点同士をつなぐ辺が9つあります。では頂点sからtまで流すことができる水の量はどうなるでしょうか?
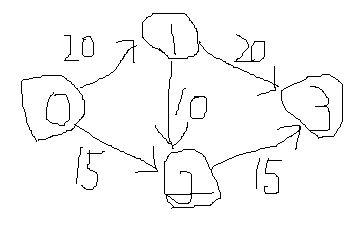
始点から終点まで流すことができるパスを求め、フローの流量を求め、通過した辺の容量をそのぶん減らす、また始点から終点まで流すことができる別のパスを求めフローを流すのを繰り返すという方法でよさそうですが、それだとうまくいかない場合があります。
上の例は簡単な図なので考えるまでもなく、答えは35です。0→1→3を20、0→2→3を15、あわせて35です。
ところが0→1→2→3というパスを最初に選択して10のフローを流してしまうと(下図)、0→1→3には10のフローを流したあと0→2→3には5のフローしか流せず合計は正しい値になりません。
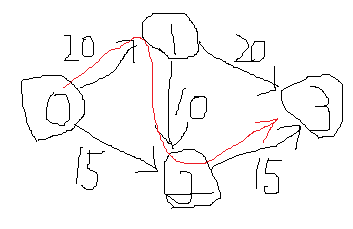
そこで鍵となるのが逆辺です。ある辺にフローを流すと、その辺の容量は流した分だけ減り、逆向きの辺の容量が流した分だけ増えるという考え方です。
この方法だと上のような要領が悪いパスを選んだとしても(下図)、0→1→3に10のフローを流して、0→2→3に5のフローを流し、0→2→1→3に10のフローを流すことができるので合計は35となり正しい値を得ることができます。
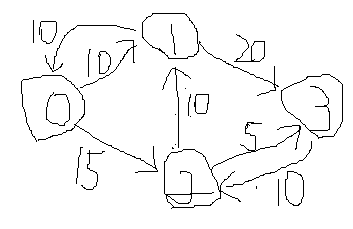
フローをどれだけ追加できてどれだけ戻すことができるかを重みつき有向グラフで表したものを残余ネットワークといいます。
下の動画の説明はわかりやすいです。
以前、C#でFord-Fulkerson(フォード・ファルカーソン)のアルゴリズムを用いて最大流問題を解く処理を実装しましたが、今回はJavaScriptで実装することにします。
実装する
まずHTML部分を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
<!DOCTYPE html> <html lang="ja"> <head> <meta charset="UTF-8"> <title>Ford-Fulkerson法で最大流問題を解く</title> <meta name = "viewport" content = "width=device-width, initial-scale = 1.0"> <style> #vertex-count, #start, #goal, #edges, #result { display: block; } </style> </head> <body> 頂点数:<input type="number" id = "vertex-count"> 始点:<input type="number" id = "start"> 終点:<input type="number" id = "goal"> 辺情報:<br> <textarea rows = "10" id = "edges"></textarea> <button onclick="calc()">計算</button> <button onclick="allClear()">クリア</button> <textarea rows = "10" id = "result"></textarea> <script src= "./index.js"></script> </body> </html> |
初期値(入力例)をセット
頂点の数と始点、終点、各辺の流せる量を指定します。どのように指定するかわかるようにページが読み込まれた段階で初期値がセットされるようにしておきます。
index.js
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
const $vertexCount = document.getElementById('vertex-count'); const $start = document.getElementById('start'); const $goal = document.getElementById('goal'); const $edges = document.getElementById('edges'); const $result = document.getElementById('result'); class Edge { constructor(from, to, capacity){ this.From = from; this.To = to; this.Capacity = capacity; } } window.onload = () => { // 初期値(入力例)をセット const text = `0 1 20 0 2 15 1 2 10 1 3 20 2 3 15`; $vertexCount.value = 4; $start.value = 0; $goal.value = 3; $edges.value = text; $result.value = ''; } |
クリアボタンがクリックされたら入力されたデータを消去します。
|
1 2 3 4 5 6 7 |
function allClear(){ $vertexCount.value = ''; $start.value = ''; $goal.value = ''; $edges.value = ''; $result.value = ''; } |
最大流を計算する
計算ボタンがクリックされたら最大流を計算します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
function calc(){ // 入力された値を取得する const n = Number($vertexCount.value); const s = Number($start.value); const t = Number($goal.value); const arr = $edges.value.split('\n'); const edgesList = []; // 各頂点から出ている辺情報を格納する配列の配列 for (let i = 0; i < n; i++) edgesList.push([]); const edges = []; // すべての辺情報を格納する配列 for (let i = 0; i < arr.length; i++){ if(arr[i] == '') continue; const arr0 = arr[i].split(' '); const from = Number(arr0[0]); const to = Number(arr0[1]); const capacity = Number(arr0[2]); const edge = new Edge(from, to, capacity); edgesList[from].push(edge); edges.push(edge); // これが「逆辺」!! edgesList[to].push(new Edge(to, from, 0)); } let ret = 0; while (true){ const path = []; // 始点から終点まで到達できるパスがあるか探す。ないなら終了 // searchPath関数は後述 if(!searchPath(s, t, edgesList, path)) break; // 見つかったパスで流せる量を求める(各辺のCapacityで最小のものがそれ) // 各辺のCapacityで最小値を探す let min = Number.MAX_SAFE_INTEGER; // 整数がとりうる最大値で初期化 for(let i=0; i < path.length; i++){ if(min > path[i].Capacity) min = path[i].Capacity; } // 残余ネットワークを更新する // 流した分だけ減らし逆辺は増やす path.forEach(edge => { edge.Capacity -= min; const edge2 = edgesList[edge.To].find(_ => _.From == edge.To && _.To == edge.From); if (edge2 != null) edge2.Capacity += min; }); ret += min; // 増やした総数を記憶しておく } // 初期の状態と残余ネットワークを比較してどの辺にどれだけ流したかを計算する let resultText = ret + '\n'; for (let i = 0; i < arr.length; i++){ const arr0 = arr[i].split(' '); const from = Number(arr0[0]); const to = Number(arr0[1]); const capacity = Number(arr0[2]); // 初期の容量 const flow = capacity - edges[i].Capacity; // 実際に流される量 console.log(`${from} → ${to}:${flow}`); resultText += `${from} → ${to}:${flow}\n`; } $result.value = resultText; // 結果を表示 } |
幅優先探索で増加道を探す
SearchPath関数は幅優先探索でs, tまでたどり着くパスを探します。あればtrue、なければfalseを返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
function searchPath(s, t, edgesList, path){ const isVisits = []; const fromEdge = []; const queue = []; queue.push(s); while (queue.length > 0){ const num = queue.shift(); isVisits[num] = true; // 終点に到達したら始点にむけて逆にたどってパスを取得する if (num == t){ const edges = []; let i = t; while (true){ const edge = fromEdge[i]; edges.push(edge); i = edge.From; if (edge.From == s) break; } edges.forEach(edge => path.push(edge)); return true; } // edge.Capacity > 0の辺をとおってまだ訪問していない頂点があるならキューに格納する for(let i=0; i<edgesList[num].length; i++){ const edge = edgesList[num][i]; if (edge.Capacity <= 0) continue; if (isVisits[edge.To]) continue; queue.push(edge.To); fromEdge[edge.To] = edge; } } // ループを抜けてしまったら s から t へたどり着くパスは存在しない return false; } |
